2.4.3. Структурная надежность

Далее в этом разделе термин "надежность" будет употребляться в узком смысле, т.е. будет иметься в виду ее количественный показатель P(t) – вероятность того, что объект не откажет к моменту времени t, или вероятность безотказной работы в течение времени .

Структурной надежностью системы (устройства) называется результирующая надежность системы (устройства) при заданной ее структуре и известных значениях надежности всех входящих в нее частей (блоков, элементов). Эти блоки, элементы, составляющие систему и показатели надежности которых известны, называются элементами расчета надежности.

В этом разделе приведены основные способы соединения элементов в системы ЯЭУ и соответствующие формулы расчета надежности этих систем.

Последовательное соединение

В случаях, когда система состоит из нескольких частей, отказ хотя бы одной любой из которых приводит к отказу всей системы, говорят, что эти части соединены последовательно. Изображают такое соединение, как показано на рис. 2.10.

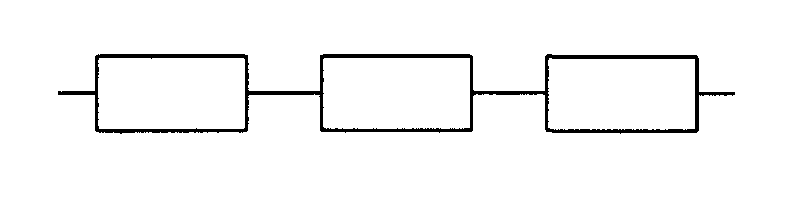
Рис. 2.10. Последовательное соединение элементов

Если отказы каждой части независимы от состояния других частей, т.е. отказ одной части не меняет надежности других, то надежность такой системы определяется как произведение надежностей отдельных частей, т.е.

где N – число элементов системы.

Надежность последовательного соединения всегда не выше, чем надежность самого ненадежного элемента.

Параллельное соединение

В случаях, когда система состоит из нескольких частей и отказ только всех частей приводит к отказу системы в целом, говорят, что эти части соединены параллельно. На рис. 2.11. изображено параллельное соеди-нение элементов.

Рис. 2.11. Параллельное

соединение элементов

Если отказы каждой части независимы от состояния других частей, то вероятность F(t) = 1-P(t) отказа системы равна произведению вероятностей отказов всех частей:

Отсюда надежность параллельного соединения есть

Таким образом, надежность параллельного соединения всегда не ниже, чем надежность самого надежного элемента.

Параллельное соединение элементов часто называют горячим резервированием, т.к. такое соединение используется для повышения надежности систем за счет одновременной работы нескольких однотипных элементов, когда для выполнения функции достаточно работы только одного из них.

Надежность системы с зависимыми элементами

Если система содержит части (блоки, элементы), выход из строя которых изменяет надежность других частей (блоков, элементов), или имеется одна причина (общая) отказов блоков, то расчет надежности системы усложняется. Кроме того, для расчета надежности системы нужно знать условные надежности элементов, определение которых требует дополнительных усилий.

В качестве примера (простейшего, но существенного для практики) рассмотрим расчет надежности системы, состоящей из двух параллельно соединенных элементов, надежности которых экспоненциальны. Для расчета надежности необходимо знать следующие значения;

₁ – опасность отказа для первого элемента;

₂ – опасность отказа для второго элемента;

₁₂ – опасность отказа первого элемента при условии, что второй элемент вышел из строя (1-я общая причина);

₂₁ – опасность отказа второго элемента при условии, что первый элемент вышел из строя (2-я общая причина).

Событие А , заключающееся в том, что система не выйдет из строя в течение времени t состоит из трех несовместных событий:

A₁ – за время t не вышел из строя ни один элемент;

А₂ – за время t первый элемент вышел из строя, а второй не вышел из строя;

A₃ – за время t второй элемент вышел из строя, а первый не вышел из строя.

Тогда для системы

Р(t) = Р(А) = Р(А₁) + Р(А₂) + Р(А₃).

Очевидно, что

Вычислим вероятность Р(А₂). Для этого найдем вероятность dP₂ того, что первый элемент выйдет из строя в интервале времени d около (0,t) , а второй элемент не выйдет из строя за время t. Для этого нужно

1) чтобы оба элемента не вышли из строя до момента  (вероятность )