2.3.2. Деревья отказов

Метод дерева отказов (ДО) представляет собой дедуктивный логический анализ причин, приводящих к отказу системы. Процедура составления ДО представляет собой последовательный и повторяющийся анализ причин. Этот анализ начинается с вершинного события, которым обычно бывает какое-либо "нет" на ДС. Часто вершинное событие называют английским словом ТОР (верх). Начиная с ТОР, для каждого события выявляются события, являющиеся его непосредственными причинами. Так продолжается до тех пор, пока не будут выявлены первичные (базовые) события (отказы), которые уже нецелесообразно разлагать на более мелкие. Причиной такой остановки обычно бывает возможность оценить каким-то образом показатель надежности элемента оборудования непосредственно, без разложения элемента на составные части. Построение ДО можно сравнить с движением от устья реки к ее истокам.

При анализе связей события с его причинами обычно используются следующие логические операторы:

1) оператор "или" (логическое сложение событий);

2) оператор "и" (логическое умножение событий).

Кроме логических операторов, элементами ДО являются:

1) вершинное событие (ТОР);

2) промежуточные события (подлежащие анализу в дереве);

3) базовые события;

4) неразвитые события (подлежащие анализу в другом дереве).

На рис. 2.6 приведены примеры изображения элементов ДО, графически представляемого в виде диаграммы, похожей на перевернутое дерево, корнем которого является ТОР.

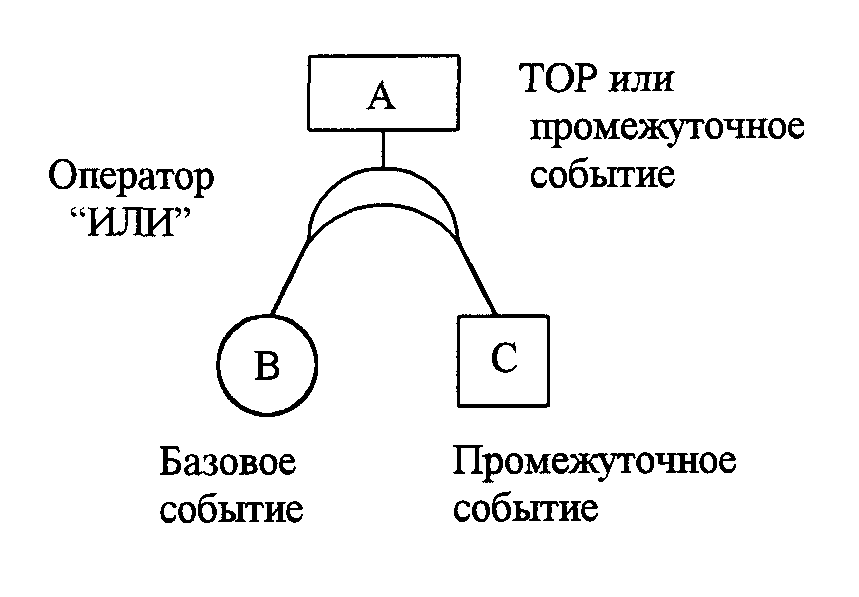
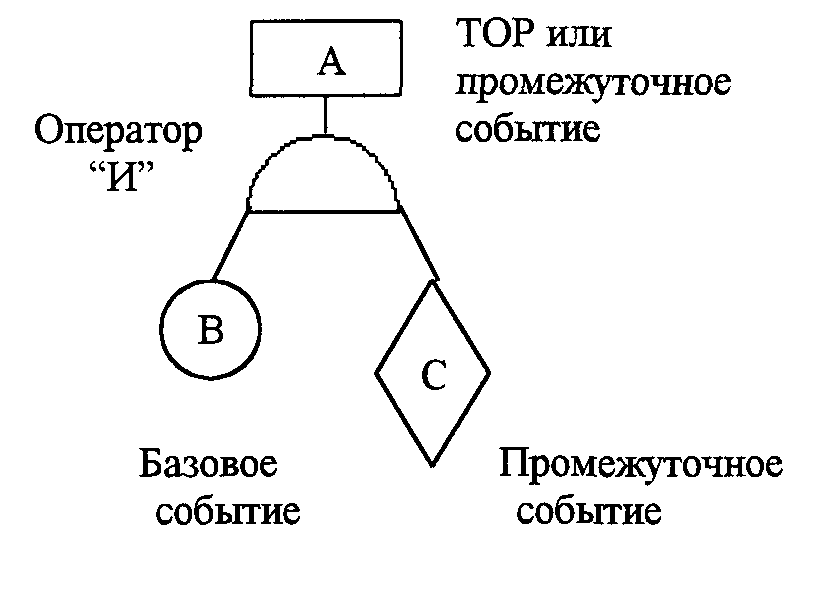
Рис. 2.6. Основные типы логической зависимости событий

Наилучший способ обучения построению ДО – решить какой-нибудь пример. Пусть

TOP=(G+X)(G+Y). (2.11)

Записанную формулу словами можно выразить примерно так: система откажет в случае, если одновременно произойдут два события – отказ элемента G или элемента X и отказ элемента G или элемента У.

П

остроим дерево отказов, соответствующее этому логическому выражению.

Рис. 2.7. Пример дерева отказов

Внимательно рассмотрев приведенное на рис. 2.7 ДО, можно увидеть, что оно построено не самым экономным образом, хотя бы потому, что на нем событие G содержится два раза.

Законы булевой алгебры позволяют сокращать деревья отказов. Наиболее употребительны два из них:

1) закон эквивалентности, который формально записывается как

А + А = А, АА=А;

2) закон поглощения, имеющий такую формальную запись

А + АВ = А.

Для сокращения построенного дерева раскроем скобки в выражении (2.11). С использованием приведенных двух законов получим:

Т ОР = GG + GY + GX + XY = G + XY.

G

Соответствующее последнему логическому выражению ДО приведено на рис 2.8.

В

Рис. 2.8. Сокращенное дерево отказов

идим, что одним логическим оператором на сокращенном ДО оказалось меньше и все базовые события на нем представлены один раз.

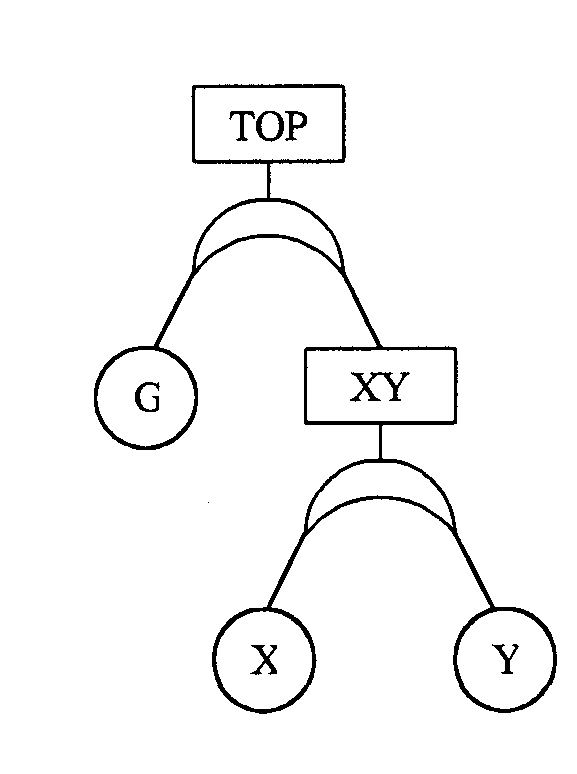
При анализе ДО существенно используются понятия критического сечения (КС) и минимального критического сечения (МКС). Критическими сечениями называются сочетания событий, самостоятельно приводящие к ТОР. Иными словами КС – это сочетания событий, соединенные операторами "или" в логическом выражении для ТОР, когда все скобки раскрыты. МКС – это КС, не содержащие никаких других КС. В рассмотренном примере КС – это G, GX, GY и XY, МКС – это G и XY.

Резюмируя изложенное выше, можно заключить, следующее: чтобы вычислить вероятность какого-либо "нет" на ДС, необходимо сформулировать соответствующий ТОР, построить ДО, сократить его так, чтобы получить все МКС. Тогда вероятность i-го "нет" можно записать так:

,

где n_i – число МКС, входящих в i-й ТОР.

Если базовые события (отказы элементов оборудования или ошибки персонала), входящие в МКС, независимы, то

,

где т_j – число базовых событий, входящих в j-e МКС; Р_k – вероятность k-го базового события.

В случае зависимости базовых событий задача вычисления вероятностей существенно усложняется, но все-таки может быть решена. Пример такого решения дан в разделе 2.4.3.