Характеристические свойства законов распределения

1. Из определения функции распределения сразу следует:

а) F(-) = 0, F(+) = 1, F(x)[0,1 ;

б) F (x) – неубывающая функция х.

2. Плотность распределения f (x) – неотрицательная функция x¹, причем

.

Любые функции, обладающие приведенными характеристическими свойствами, могут считаться законами распределения некоей случайной величины, вне зависимости от физического содержания модели, из которой они получены.

ЧИСЛОВЫЕ ХАРАКТЕРИСТИКИ СЛУЧАЙНЫХ ВЕЛИЧИН

Законы распределения – обычные детерминированные функции своих аргументов и с ними можно оперировать по обычным правилам математического анализа. Например, можно задать некоторую функцию () случайной величины , имеющей плотность распределения f(), и сформировать такой функционал

.

Этот функционал называется математическим ожиданием (средним значением) функции (). J –детерминированная (неслучайная) величина. Различные функционалы J – числовые характеристики случайных величин.

В принципе, функцию () можно задавать любого вида. В теории вероятностей, математической статистике и теории надежности наиболее распространено использование следующих функций:

¹Замечания: 1) плотность распределения – необязательно непрерывная функция; 2) плотность распределения - обязательно немонотонная функция.

 () =  (M, – среднее значение случайной величины ,),

 () =² (M ² – второй начальный момент случайной величины );

 () = ( — М)² (М( — М)² = D_ – дисперсия, или второй центральный момент, случайной величины ).

Эти три функции здесь также широко используются. М определяет средневзвешенное положение случайной величины на числовой оси, a D_ – средний квадрат ее разброса около этого положения.

2.3. Деревья отказов и деревья событий

При проведении ВАБ ЯЭУ в мировой практике широко применяется методология деревьев отказов (ДО) и деревьев событий (ДС). Она позволяет наиболее полно проследить причинно-следственные связи между событиями, могущими привести в определенном их сочетании к аварии ЯЭУ.

В общем плане можно сказать, что ДС строятся от причины к следствию, а ДО – от следствия к причине. При этом, ДС помогают выполнить детерминистическую часть ВАБ, позволяя оценить круг всех опасностей, которые могут возникнуть при работе ЯЭУ, и определить необходимый минимум систем безопасности (СБ) для их предотвращения. ДО помогают выполнить оценки вероятностей реализации опасностей из-за отказов как систем нормальной эксплуатации ЯЭУ, так и СБ.

2.3.1. Деревья событий

Деревья событий строятся для того, чтобы

1) определить системы безопасности, которые требуются для безаварийной работы ЯЭУ;

2) как следует понять все опасности при возникновении аварий, найти как можно более полный их набор или набор всех устройств, которые не сработают при авариях, и управлять авариями, если они возникли;

3) защитить проект новой ЯЭУ или какой-либо модернизации оборудования действующей ЯЭУ.

Построение ДС всегда начинается с составления перечня исходных событии (ИС), которые постулируются из событий трех классов:

а) внутренние отказы,

б) внешние события,

в) ошибки персонала (человеческий фактор).

Исходные события последнего класса формулировать очень сложно, т.к. на них влияет очень большое количество факторов, например, подготовка, опыт, условия стресса, располагаемое для размышлений и действий время, вмешательство начальства, личные проблемы, прием лекарств, алкоголь и др.

Необходимо составлять наиболее полный список исходных событий. Он составляется из событий:

а) взятых из опыта эксплуатации этой ЯЭУ или аналогичных (если анализируется проект новой);

б) на которых настаивают регулирующие органы;

в) которые определяются необходимостью посмотреть есть ли еще другие события, о которых не догадались регулирующие органы.

Этот перечень может быть удовлетворительным или нет в зависимости от того, удовлетворяет ли он все заинтересованные стороны (разработчиков, регулирующие органы, заказчиков работы, движение "зеленых" и т.д.).

Разумеется, всегда остается вопрос – является ли составленный перечень исходных событий исчерпывающим.

Техника построения деревьев событий состоит в следующем. Постулируется какое-либо принадлежащее перечню исходное событие. Оно считается событием первого уровня. Далее смотрят, что должно произойти после исходного события, т.е. какие системы должны быть задействованы и какие функции они должны выполнить в первую очередь. Это – второй уровень. Далее смотрят, в зависимости от успеха или неуспеха первой очереди, какие системы должны быть задействованы и какие защитные функции должны быть выполнены во вторую очередь. И так далее вплоть до конечного события (состояния).

Таким образом, ДС представляет собой логическую диаграмму, которая определяет множество возможных конечных состояний ЯЭУ, каждое из которых может реализоваться через цепочку (сочетание, комбинацию) промежуточных событий (состояний). Разумеется, учитываются события, которые могут повлиять на сценарий развития аварии при постулированном ИС.

В соответствии с требованиями ОПБ-88/97 обычно интересуются двумя конечными событиями:

1) повреждение активной зоны реактора сверх оговоренных в технической документации допустимых пределов;

2) выброс р/а веществ сверх допустимых норм.

В качестве промежуточных могут использоваться следующие события:

- выполнение или невыполнение функций системами безопасности;

- правильные или ошибочные действия персонала и т.д.

Г

рафически дерево событий изображается в виде таблицы состояний и диаграммы событий в форме разомкнутого бинарного графа. Основным элементом ДС является изображенный на рис. 2.4.

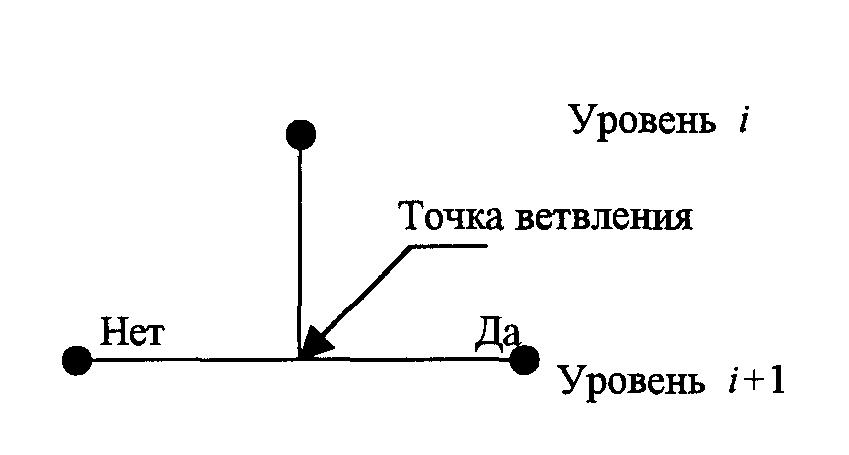
Рис. 2.4. Основной элемент дерева событий

Здесь точка ветвления означает, что на очередном i+1-м уровне события могут развиваться в двух направлениях: или требуемые на этом уровне системы выполняют свои функции (направление "да"), или (из-за отказов оборудования, ошибок персонала и т.п.) они эти функции не выполняют (направление "нет"). Каждому из этих направлений соответствует свое продолжение развития событий (события i+2-го уровня и т.д.).

Пример. На рис. 2.5 изображено укрупненное ДС для исходного события "течь в основном контуре охлаждения реактора" (1-й уровень). Понятно, что при таком исходном событии первоочередной мерой является останов реактора (2-й уровень). Вне зависимости от того, удалось или нет сразу заглушить реактор, требуется организация аварийного охлаждения реактора и снятия остаточного тепловыделения, когда реактор будет все-таки заглушен (событие 3-го уровня). Далее, если конечным событием считается "выброс р/а веществ сверх допустимых норм", то требуется герметизация помещений и/или контайнмента, если он есть (4-й уровень).

На любом промежуточном уровне может наступить успех или неудача при выполнении соответствующей функции. Последовательности (пути на графе), могущие привести к реализации конечного события, отмечены знаком *.

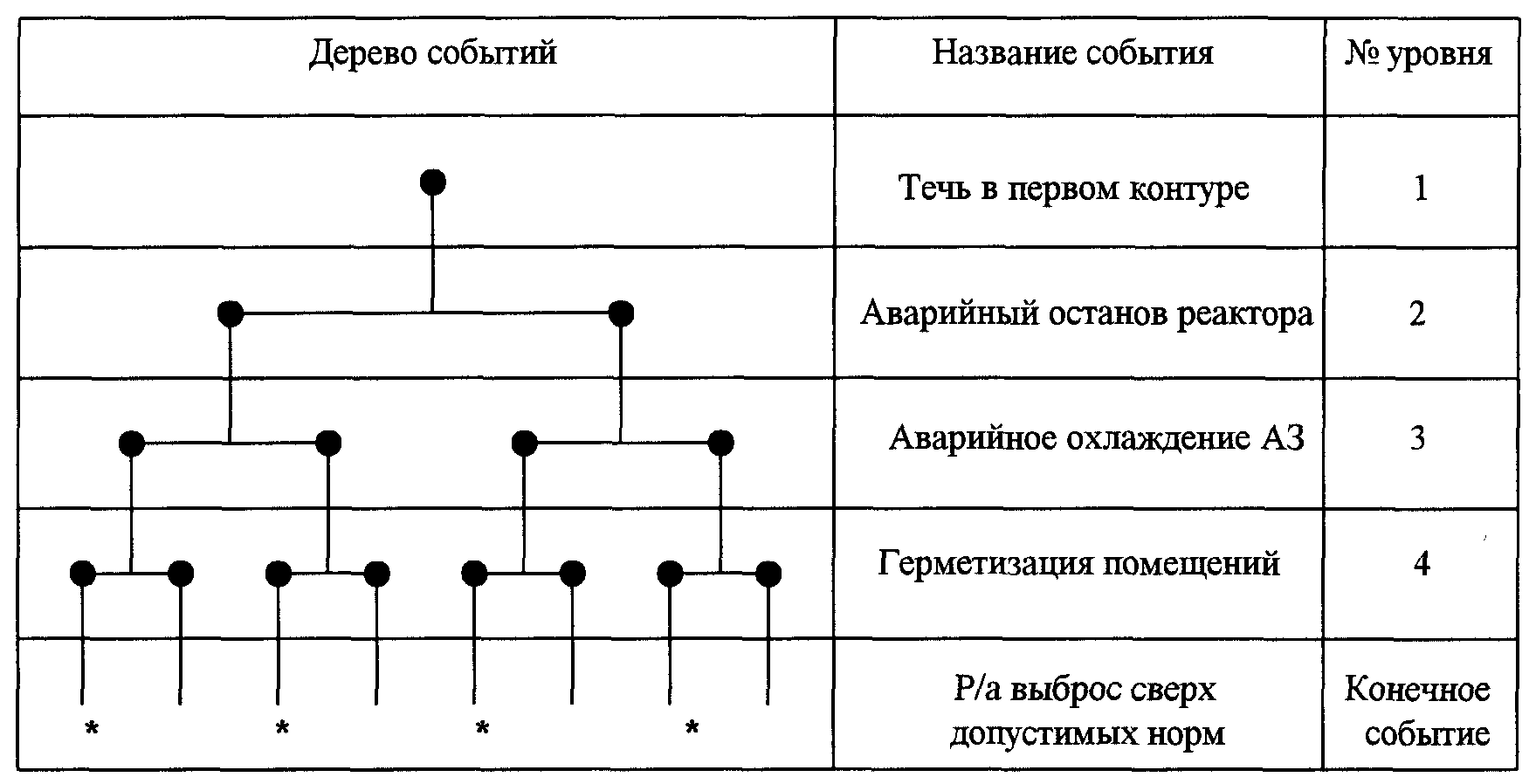
Рис. 2.5. Пример дерева событий

Из приведенного примера можно увидеть одно из возможных приложений ДС: составив отношение числа отмеченных знаком* концов ДС к полному их числу, можно приблизительно (очень грубо и с большим запасом) оценить сверху вероятность реализации интересующего события. Такая грубая оценка может использоваться при сравнении различных вариантов технического решения по компоновке конкретной ЯЭУ.

Разумеется, рассмотренный пример – учебный и такой, чтобы ДС заняло не так много места на странице. В реальных ситуациях число уровней может достигать нескольких десятков. Значит, рассматривается примерно соответственное количество функций и/или систем безопасности.