2.2.4. Формула Байеса. Проверка гипотез

Пусть А – произвольное событие, события В₁,...,В_n попарно несовместны, Р(B_k )> 0, k = 1,…,n и А  B₁+ В₂ + ... + В_n. Соотношения между событиями иллюстрирует рис. 2.2.. Событие А можно представить в виде следующей суммы попарно несовместных событий:

А = AB₁ + AB₂ + ... + АB_n.

Воспользовавшись теоремой сложения и теоремой умножения вероятностей, получим формулу

, (2.4)

которая называется формулой полной вероятности.

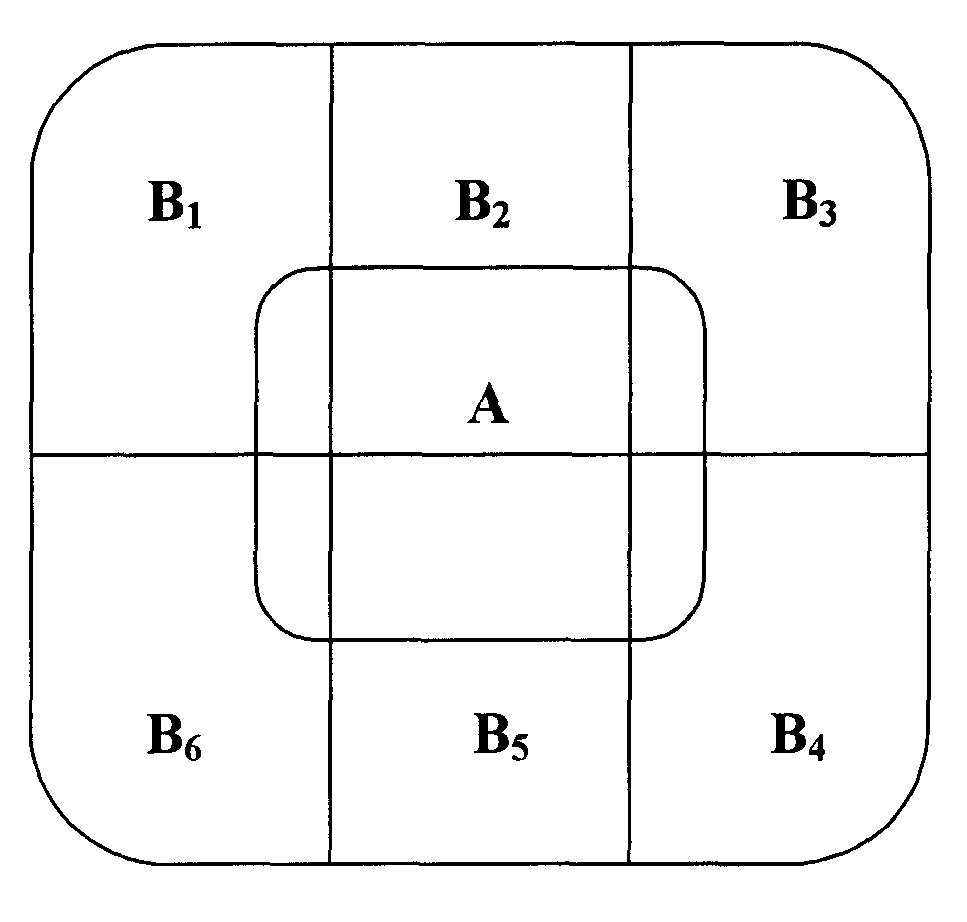
Рис. 2.2. Иллюстрация соотношения между событиями для n = 6 при выводе формулы полной вероятности

Поставим следующую задачу. Предположим, относительно результата (исхода, события) некоторого опыта можно высказать несколько попарно несовместных гипотез B₁,...,В_n , которые образуют полную группу, т.е. не могут быть дополнены какими-либо другими, и можно считать, что

 = В₁ + В₂ + ... + В_n. Вероятности этих гипотез (исходов, событий) до опыта известны и равны соответственно Р(В₁),…,Р(В_n). Произведен опыт, в результате которого наблюдалось появление некоторого события А. Спрашивается: как следует изменить вероятности выдвинутых гипотез в связи с появлением этого события?

Здесь, по существу, речь идет о том, чтобы найти условную вероятность каждой гипотезы относительно события А.

Из теоремы умножения вероятностей имеем

,

откуда

. (2.5)

Выражая Р(А) через формулу полной вероятности (2.4), имеем

. (2.6)

Формула (2.6) носит название формулы Байеса или теоремы гипотез.

Замечание по поводу использования формулы Байеса. Она применяется при оценке показателей надежности изделий по результатам испытаний. Ее имеет смысл применять, когда в правой части все вероятности известны. То есть до опыта они были, например, вычислены по какой-либо вероятностной схеме или найдены из каких-либо физических соображений, или получены на основе предыдущего опыта и т.п.

2.2.5. Независимость событий

События А и В называются независимыми, если

Р(АВ) = Р(А)Р(В). (2.7)

Отсюда следует, что при Р(А) > 0 и Р(В) > 0 независимость А и В эквивалентна любому из равенств

, .

Вообще

P(A₁A₂...A_n)=P(A₁)P(A₂)...P(A_n), (2.8)

что эквивалентно

.

Необходимо заметить, что из попарной независимости событий А, В, С и т.д. нe следует их независимость в совокупности, т.е., например, из Р(АВ) = Р(А)Р(В), Р(BС) = Р(В)Р(С), Р(АС) = Р(А)Р(С) не следует, что

Р(АВС) = Р(А)Р(В)Р(С).

Если математическая модель, описывающая реальный опыт, подобрана достаточно хорошо, то независимым событиям реального опыта соответствуют события модели, независимые в смысле определений (2.7) или (2.8).

Заметим, понятия несовместности и независимости событий А и В не являются эквивалентными. Несовместность событий – отсутствие общих элементов в соответствующих множествах. Независимость не означает несовместность и наоборот. Более того, несовместные события всегда зависимы. Это иллюстрирует рис. 2.3.

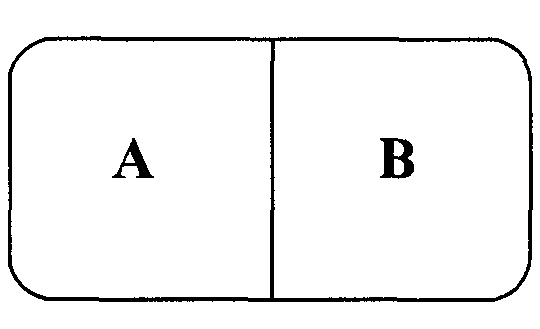
Р(А) > 0 и Р(В) > 0,

т.е. Р(А)Р(В) > 0, но Р(АВ)= 0.

Рис. 2.3. Иллюстрация несовместности и независимости событий