6 Расчет переходных процессов
Расчет переходных процессов при пуске и торможении произведем по методике, изложенной в [6]. Суммарный момент инерции привода определяется как
,
(6.1)
где Jдв - момент инерции двигателя (кг.м2);
Jпр - момент инерции исполнительного механизма, приведенный к валу двигателя (кг м) – определён в п 1.2.
Момент инерции двигателя определяем как (6.2)
.
В этой формуле
- плотность стали ротора (по справочнику
плотность электротехнической стали
равна 7800 кг/м2);
l1 – длина сердечника статора (м);
l2 – длина сердечника ротора (м);
Di1 – внутренний диаметр сердечника статора (м);
- односторонний
воздушный зазор между статором и ротором
(мм).
кг.м2.
Тогда момент инерции привода J по формуле (6.1) составит
кг.м2.
(6.3)
6.1 Расчет переходных процессов при пуске электродвигателя
Для расчета переходных процессов при пуске линеаризуем механические характеристики привода. В результате получим прямые, изображенные на рисунке 1, по которым и будем вести расчет.
Время работы на каждой i-ой ступени можно определить как
,
(6.4)
где Tм_i - электромеханическая постоянная времени привода на i-ой ступени (с);
уст_i
- угловая скорость двигателя на i-ой
степени, соответствующая статическому
моменту (рад/с);
нач_i, кон_i - начальная и конечная угловые скорости двигателя на i-ой ступени (рад/с).
,
(6.5)
где M1,M2 - пиковый и переключающий моменты (Н.м).
Временные зависимости скорости и момента будем рассчитывать, используя следующие выражения:
,
(6.6)
.
(6.7)
Используя рисунок 5 и формулы (6.4) и (6.5), для первой ступени получим:
Н.м,
Н.м,
рад/с,
рад/с,
рад/с.
с,
с.
Подставляя в
выражения (6.4)
и (6.5) значения времени от нуля до tп_1,
рассчитываем зависимости
и М1(t).
,
.
Данные расчета сводим в таблицу 6.
Таким же образом проводим расчеты для других характеристик.
Для второй ступени:
Н.м,
Н.м,
рад/с,
рад/с,
рад/с.
с,
с,
,
.
Данные расчета сводим в таблицу 7.
Для третьей ступени:
Н.м,
Н.м,
рад/с,
рад/с,
рад/с.
с,
с,
,
.
Данные расчета сводим в таблицу 8.
Разгон по естественной характеристике:
Так как разгон на естественной характеристике теоретически будет длиться бесконечно долго, то за конечную примем скорость, которая на 3% меньше статической.
Н.м,
Н.м,
рад/с,
рад/с,
рад/с.
с,
с,
,
Данные расчета сводим в таблицу 9.
Таким образом, время пуска tп из неподвижного состояния до установившейся скорости составит
с.
(6.8)
Таблица 6 Таблица 7
s |
ω, рад/с |
М, Н.м |
0,00 |
0,00 |
1380 |
0,05 |
15,38 |
1209 |
0,10 |
28,69 |
1060 |
0,15 |
40,23 |
931,5 |
0,20 |
50,23 |
820,07 |
0,25 |
58,89 |
723,54 |
0,27 |
62,00 |
698,85 |
s |
ω, рад/с |
М, Н.м |
0,00 |
62 |
0,00 |
0,01 |
65,25 |
1308 |
0,02 |
68,271 |
1223 |
0,03 |
71,078 |
1143 |
0,04 |
73,687 |
1,07 |
0,05 |
76,112 |
1001 |
0,06 |
78,365 |
936,82 |
0,07 |
80,459 |
877,55 |
0,08 |
82,405 |
822,48 |
0,09 |
84,213 |
771,29 |
0,10 |
85,894 |
723,72 |
0,107 |
87,00 |
695,00 |
Таблица 8 Таблица 9
s |
ω, рад/с |
М, Н.м |
0,00 |
87,00 |
1400 |
0,01 |
89,99 |
1200 |
0,02 |
92,52 |
1030 |
0,03 |
94,67 |
888,01 |
0,04 |
96,48 |
766,82 |
0,05 |
98,00 |
685,40 |
s |
ω, рад/с |
М, Н.м |
0,00 |
98,00 |
1400 |
0,05 |
99,57 |
402,24 |
0,10 |
100,00 |
169,11 |
0,15 |
101,01 |
114,65 |
0,167 |
101,20 |
105,16 |
По результатам таблиц 6 - 9 строим временные зависимости момента M(t) и скорости (t) на рисунках 6 и 7 соответственно.
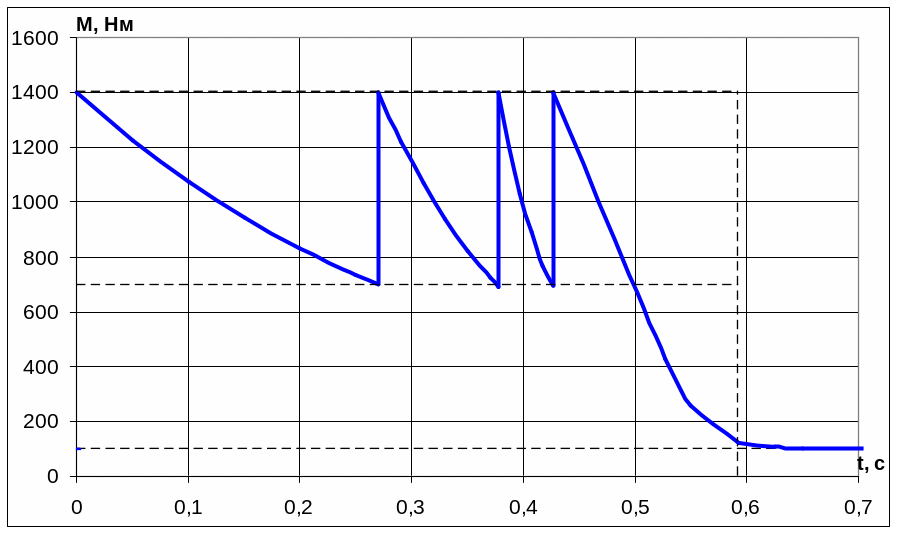
Рисунок
6 Кривая изменения момента при пуске
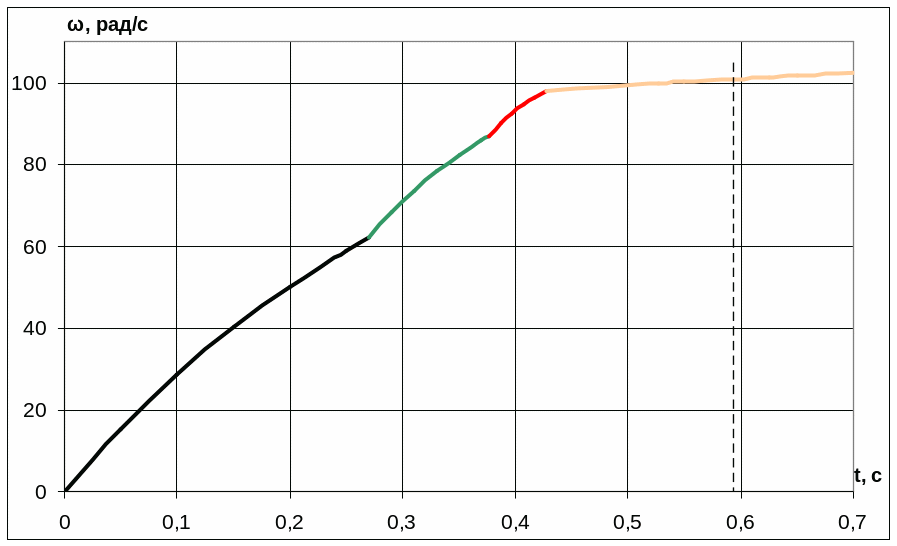Рисунок 7 Кривая
изменения скорости при пуске