2.4.2.Разложение в ряд Фурье

Если x_a(t) - периодическая функция, заданная на интервале [а, b], то ее можно представить в виде бесконечного ряда по синусам и косину­сам

где коэффициенты Фурье А_n и В_n задаются выражениями

Если x_a(t)-комплекснозначная периодическая функция, заданная на [а, b], то ее можно разложить в комплексный ряд Фурье:

где f ₌ 1/(b- а). В данном случае функция x_a(t) представлена в виде суммы по положительным и отрицательным частотам. Если x_a(t)-вещест­венная периодическая функция, то она имеет вещественный ряд Фурье с коэффициентами А_i и B_i, которые связаны с C_i. Пусть при i < 0 A_-i = A_i,B_-i=-B_i. Тогда справедливо следующее:

2.4.3.Дискретное преобразование Фурье

С пектром X(е ^jωТ) дискретного сигнала называют прямое преобразование Фурье дискретной последовательности х(пТ), n = 0,1, 2.....

Это соотношение получается из интегрального преобразования заменой t на пТ.

О братное преобразование Фурье для дискретной последовательности имеет вид

Дискретное преобразование Фурье представляет собой частный случай z-преобразования.

то есть преобразование Фурье представляет собой z-преобразование, вычисленное на единичной ок­ружности z-плоскости (при z=e ^jωt,φ=ωT, r=1).

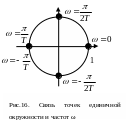
Н а рис.16 показаны единичная окружность z-плоскости и соответствие некоторых ее точек оп­ределенным частотам ω.

Например, при ω=π/2T,

С оответствующие формулы для нормированных частот получаются после подстановки ωT=2πfT=2πf̃ :

На рис.17 показаны единичная окружность z-плоскости и соответствие некоторых ее точек оп­ределенным нормированным частотам. Например, при f̃=0.5, е ^j2πf̃=e^jπ=-1.

Спектр является периодической функцией по частоте с периодом, равным частоте дискретизации ω_D = 2π/T, поскольку e ^jωT=e ^{j(ω+k∙2π/T)T}, k=0,±1,±2… Модуль и аргумент спектра также являются периодическими функциями с тем же периодом.

Если x(1), x(2), ..., x(N-1) - произвольные вещественные числа, то их можно представить в виде конечных сумм, используя формальную запись

n = 0,...,N-l.

Верхним преде­лом суммирования является не N/2, а целая часть числа N/2, но обычно используется более короткое обозначение. Так, для нечетного N вместо N/2 следует брать (N — 1)/2. Если N четное, член b_N/2 нужно опустить. Числа a_k и b_k определяются по формулам

Последовательности чисел а и b называются конечными или дискретны­ми косинус-преобразованием и синус-преобразованием Фурье набора чисел x_n, а сам набор x_n называется обратным конечным (дискретным) преобра­зованием Фурье наборов а и b. Для обозначения дискретного преобразо­вания Фурье часто используют сокращение ДПФ.

Е сли величины x_n представляют собой набор N комплексных чисел, то комплексным дискретным преобразованием Фурье для этого набора является другой набор X_n. Числа x_n и X_n связаны парой формул:

n=0,1, …N-1.

Элементы набора X_n определены для частот 0 до N — 1. Если величины x_n представляют собой набор вещественных чисел, то у этого набора есть как комплексное дискретное преобразование Фурье, так и дискретные косинус- и синус-преобразования Фурье a_k, b_k, k = 0,..., N/2. Они связаны между собой:

Х₀=а₀, Х_k=(a_k - jb_k)/2, 1≤k≤N/2.

кроме случая четного N, в котором надо опустить 1/2 в X_N/2. Остальные значения Х_k являются комплексно сопряженными к числам из первой половины набора, и их обычно игнорируют. Конкретно,

Х_k = (a_k + jb_k)/2, 1≤k≤N/2.