28

2.Преобразования цифровых сигналов

2.1.Математическое представление цифровых сигналов.

Сигнал — это физический процесс (например, изменяющееся во времени напря­жение), отображающий некоторую информацию.

Аналоговый сигнал описывается непрерывной (или кусочно-непрерывной) функ­цией времени х_а (t). Аргумент и функция могут принимать произвольные значения в определенном интервале: tє[t₁,t₂], x_a[t]є[x₁,x₂],

Дискретный сигнал (физически реализуемый) описывается решетчатой функцией х(пТ), п = 0, 1, 2,..., значения которой определены только при дискретных равноот­стоящих друг от друга значениях неза­висимой переменной. При этом предпо­лагается, что х(пТ) = 0 при n < 0.

На рис. 10 приведены графические изображения аналогового сигнала

_xa(t)=e^-αt, α > 0

и соответствующего дискретного сигнала

_x(nT)=e^-αnT, п = 0,1,2.....

Рис. 10. Дискретный сигнал

Значения декретного сигнала х(пТ) называются отсчетами сигнала.

Они представляют собой выборки ис­ходного аналогового сигнала в моменты времени t = пТ, п = 0, 1, 2,...

_{x(nT)= xa(t)|t=nT,} n = 0, 1,2, ... .

Отсчеты дискретного сигнала могут принимать произвольные значения в опреде­ленном интервале: x(nT)є[x₁,x₂]. Они отстоят друг от друга на величину Т, назы­ваемую интервалом дискретизации.

П оскольку дискретный сигнал описывается последовательностью чисел, термин "решетчатая функция х(пТ) заменяют термином "дискретная последователь­ность х_п:

х_n=х(пT), п = 0,1,2..... (1)

считая, что параметр Т фиксирован.

Выборки сигнала берутся с интервалом Т, т. е. с определенной частотой, назы­ваемой частотой дискретизации f_D:

f_D=1/T. (2)

Важным параметром гармонического сигнала является нормированная частота f̃ , определяемая как отношение частоты к частоте дискретизации:

f̃ =f/f_D (3)

Пример. Задан аналоговый сигнал x_a(t) = cos 2πf·t (рис. 11).

С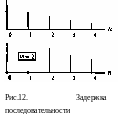 оответствующий дискретный сигнал x_n при за­данной частоте дискретизации f_D=1/T имеет вид:

х_n= cos2πfnT= cos2πfn/f_D= cos2π f̃ n

Последовательности бывают конечной и бесконечной длины. Их называют соот­ветственно конечными и бесконечными последовательностями.

Отсчеты х_n не задержанной физически реализуемой конечной последовательно­сти длины N могут принимать не нулевые значения только при n = 0, 1, 2...N-1, а бесконечной последовательности — для всех п.

Для описания последовательностей используются различные способы. Например, последовательность из примера 1.1 можно представить в

• аналитическом виде х_n = cos2π f̃ n, n = 0, 1, 2, ...

• в виде последовательности отсчетов х_п = {х₀, х₁, х₂, х₃,... } При этом предполагает­ся, что х_n = 0 при n < 0.

Задержанной на m интервалов дискретиза­ции Т последовательностью называется последовательность y_n = х_n-m . При этом y_n=0 при п<т (рис. 1.3).

В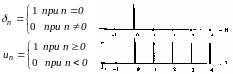 ажное значение в теории и практике цифровой обработки сигналов имеют две последовательности (рис. 1.4):

Единичный импульс

Единичный скачок

Произвольную последовательность х_п можно представить с помощью единичного импульса в виде:

, n = 0,1,2,. (4)

Например, при n = 2 x₂=x₀δ₂+x₁δ₁+x₂δ₀+x₃δ_-1+…= x₀·0+x₁·0+x₂·1+x₃·0+…= x₂

поскольку только δ₀=1, а остальные δ_n-k= 0.

2.2.Z-преобразование

Z-преобразование является методом представления (описания) дискретных последовательностей и дискретных систем.

Прямое z-преобразование определяет z-образ дискретной последовательности.

Обратное z- преобразование определяет последовательность по ее z-образу.

В дальнейшем мы будем рассматривать физически реализуемые последователь­ности (отсчеты которых равны нулю для n < 0).

Для последовательности x_n, n = 0, 1, 2, ..., z-преобразование X(z) определяет­ся соотношением

(5)

где z=r·e ^jφ=r · (cosφ+i·sinφ)=a+i·b, — комплексная переменная,

a=r· cosφ, b= r· sinφ, r=(a²+b²)^½ , tg φ=b/a

(cosφ+i·sinφ)ⁿ=cos nφ+i·sin nφ

И з уравнения (5) следует, что z-преобразование переводит дискретные последовательности из временной области в комплексное, называемую z-плоскостью (рис.13). При этом число z определяет положение некоторой точки Р в z-плоскости, модуль r комплексного числа z – длину отрезка ОР, а аргумент φ – угол между положительным направлением вещественной оси и направлением отрезка ОР.

Z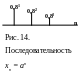 -преобразование дискретной последовательности задает функцию X(z), значения которой определены для какого-либо множества точек этого комплексного пространства.

Рассмотрим, например, последовательность х_п = аⁿ , п = 0, 1, 2..., причем |a|< 1. Последовательность х_п при а = 0,8 изображена на рис.14.

Z -образ последовательности определяется с помощью (5):

П олучили ряд, являющийся геометрической прогрессией со знаменателем q=a/z и постоянным коэффициентом c=1, т.е. ряд вида ∑с·qⁿ. По определению сумма этого ряда имеет фиксированное значение (т.е. ряд сходится), только когда |q|<1, и она равна:

Следовательно, при условии, что |a/z|<1 или |a|/r<1, z-преобразование для рассмотренного случая определится как:

И з рассмотренного примера видно, что комплексная функция X(z) определена не для всех значений переменной z, а лишь для тех значений z, для которых выполняется условие |a/z|<1, т.е. для которых ряд (5) сходится. Условием сходимости ряда (5) является

(6)

Множество значений z, для которых ряд (5) сходится, называют областью схо­димости. Область ходимости определяется радиусом сходимости R. Он равен ра­диусу круга в z-плоскости, вне которого выполняется условие (6). Величина R зави­сит от положения особых точек (полюсов) функции X(z).

В рассмотренном нами случае функция X(z) определена только для значений |a/z|<1 или |a|<|r|, т.е. область ходимости лежит вне круга радиуса R=а.

Удобным способом графического представления X(z) является изображение полюсов z^*_k, k=1,2,…,M и нулей z⁰_l, l=1,2,…,N функции в z-плоскости, называемое картой нулей и полюсов.

Полюс — это корень полинома в знаменателе, а нуль — корень полинома в числителе функции. Если полином имеет вещественные коэффициенты, то его корни могут быть вещественными и/или комплексно-сопряженными. При определении значений нулей и полюсов в z-плоскости целесообразно преобразовать функцию к виду без отрицательных степеней

В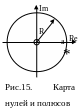 рассмотренном нами примере для определения нулей и полюсов преобразуем X(z) к виду без отрицательных степеней z: X(z) = z/(z - а). Функция X(z) имеет один ноль в точке z⁰_l=0 и один полюс в точке z^*_k=а (рис.15).

С помощью обратного z-преобразования можно определить дискретную последовательность по ее z-образу

(7)

г де С — контур, расположенный в области сходимости подынтегральной функции X(z)z^n-1 и охватывающий начало координат. Контурный интеграл (7) удобно вычислять с помощью теоремы о вычетах: контурный интеграл равен сумме вычетов подынтегральной функции в полюсах z=z^*_k k=1, 2...., М, расположенных в области, охватываемой контуром С:

(8)

В случае простого полюса вычет в точке z=z^*_k определяется соотношением

(9)

В рассмотренном нами примере для того, чтобы найти последовательность х_n, соответствующую z-образу последовательности X(z) = z/(z - а), выполним следующие действия. Определим подынтегральную функцию:

Н айдем все полюсы подынтегральной функции. В данном случае имеется один полюс в точке z^*₁=а. Вычислим вычет в точке z^*₁=а по формуле (9), определив тем самым последовательность х_n: