1.4.Цифро-аналоговое преобразование и квантование

Цифровой сигнал, представленный п + 1 битами параллельно, в не­который фиксированный момент времени, имеет величину D=(a_n a_n-1 … a₁ a₀).

Если не рассматривать дробные числа и числа со знаком, то аналого-цифровое преобразование описывается следующим простым соотношением:

где V_A — преобразуемое входное напряжение, V₀ — минимально разли­чимый шаг напряжения, на которое может увеличиваться V_A, Q — остаток, который возникает из-за ошибки квантования. D может принимать только конечное число дискретных значений.

Р азрешающая способность АЦП равна отношению максимального вы­ходного напряжения к шагу приращения напряжения V₀, т.е.:

Разрешение АЦП должно быть достаточно высоким, что­бы обеспечить требования, предъявляемые к точности измерительной сис­темы.

Задача аналого-цифрового преобразователя (АЦП) состоит в том, чтобы найти такие значения битов а, при которых ошибка квантова­ния Q минимальна.

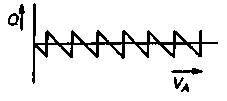
Рис. 3. (а) Передаточная характеристика АЦП. (б) Ошибка квантования Q, которой всегда сопровождается аналого-цифровое преобразование.

Д аже если взятие выборок и аналого-цифровое преобра­зование выполняются идеально, то все равно нам придется иметь дело с ошибками квантования. На рис. 3(б) эта ошибка была показана для случая, когда входной сигнал V_A линейно нара­стает. Ошибка квантования равна: Q=ΔV_i=|V'_A - V_A|, где V'_A — аналоговый эквивалент двоичного выходного сигнала на выхо­де АЦП. Так как двоичное слово D=(a_n a_n-1 … a₁ a₀) содержит n+1 битов, наи­меньшее приращение равно:

где V_max - максимальное входное напряжение на входе АЦП.

Аналого-цифровой преобразователь на рис. 3 вносит так называемую «ошибку округления». При таком квантовании максимально возможная ошиб­ка определяется неравенствами:

-V₀ /2 ≤ Q ≤ V₀ /2

Максимальная ошибка квантования при округлении рав­на плюс или минус половине значения единицы в младшем разряде. При усечении ошибка квантования лежит в пределах

0 ≤ Q ≤ V₀

Объединяя все эффекты квантования на пути следования сигнала в сис­теме сбора данных, мы можем представить их как результат действия одного блока, назвав его «устройством квантования». Приведенными выше соотно­шениями описывается нелинейная модель такого устройства квантования как в случае округления, так и при усечении (рис. 4). Такую нелинейность трудно описать аналитически. Поэтому часто пользуются стохастической моделью, пред­ставленной на рис. 4(d). Согласно этой модели устройство квантования содержит источник аддитивного шума квантования; выходной сигнал равен сумме входного сигнала V_A и шума квантования V_N. Шум квантования имеет плотность распределения вероятностей f(Q), изображенную на рис. 4(е). Считается, что Q равновероятно принимает все значения между +V₀ /2 и - V₀ /2; распределение вероятностей является равномерным. Среднее значение Q равно нулю, а дисперсия определяется соотношением:

Т аким образом, среднеквадратическое значение (стандартное отклоне­ние) V_N добавляемого шумового сигнала равно:

Рис. 4. Устройство квантования с источником шума квантования на пути следования сигнала в системе сбора данных, (а) Устройство квантования как нелинейный элемент с характеристикой, изображенной на рис. (б), и ошиб­кой квантования Q, показанной на рис. (с), (d) Стохастическая модель устрой­ства квантования. Добавляемый шум V_N имеет плотность распределения веро­ятностей, приведенную на рис. (е).

Рис. 5. Влияние шума квантования на отношение сигнал/шум S/N для си­нусоидального сигнала с амплитудой, составляющей α-ю часть максимально­го сигнала V_max на входе АЦП.

Отношение сигнал/шум (S/N) вследствие ошибки квантования в случае синусоидального сигнала с пиковым значением αV_max (0≤α≤1) равно

S/N=6α²(2ⁿ⁺¹-1)²

Это соотношение иллюстрируется графиком на рис. 5, где отношение сигнал/шум S/N указано в логарифмическом масштабе (в дБ). Из графика ясно видно, что важно подавать на вход АЦП возможно больший сигнал (наибольший, при котором еще не происходит ограничения). Также видно, что при увеличении разрешающей способности АЦП на 1 бит значение S/N растет на 6 дБ.

Шум квантования в АЦП не является единственным источником оши­бок квантования в системе сбора данных. Цифровой процессор обрабатыва­ет сигнал, оперируя только со словами конечной длины. Из-за этого также возникают ошибки квантования, которые становятся совсем большими, когда применяется процессор «с фиксированной запятой» и в операциях перемножения. Важно, чтобы число перемножений при обработке сигнала было возможно меньшим, и сами перемножения рас­полагались возможно ближе к месту получения конечного двоичного ре­зультата.

В заключение можно сказать, что квантование в системе сбора и обра­ботки данных приводит к возникновению шума, который

- добавляется к квантованным составляющим на выходе;

- имеет равномерное распределение вероятностей по величине;

- не коррелирован с самим сигналом.