Оформление отчета о проделанной работе

Условно лабораторные работы можно разделить на измерительные и наблюдательные. Для каждого вида работ предлагаются единые формы отчета, приводимые ниже.

Измерительная лабораторная работа:

1. номер работы;

2. наименование работы;

3. цель работы;

4. чертеж (если требуется);

5. формулы для определения искомых величин и их погрешностей;

6. таблица с результатами измерений и вычислений;

7. окончательный результат, вывод и пр. (согласно цели работы).

Наблюдательная лабораторная работа:

1. номер работы;

2. наименование работы;

3. номер опыта;

4. цель опыта;

5. методика проведения опыта;

6. результаты наблюдения;

7. вывод;

8. общий вывод о проделанной работе (если требуется).

Лабораторная работа № 1

Расчет и измерение скорости шара, скатывающегося по наклонному желобу

Цель работы: Рассчитать конечную скорость шара, скатывающегося с на­клонного желоба. Результат расчета проверить экспериментально.

Оборудование: штатив; длинный желоб с углом раствора 90°; шар радиусом R, меньшим ширины l одной стороны желоба; линейка измерительная; секундомер.

Теоретические основы работы

Для шара, скатывающегося с наклонного желоба высотой h, на основании закона сохранения энергии можно записать:

(1)

где т — масса шара, v и ω — линейная и угловая скорости шара в данный момент времени, — момент инерции шара от­носительно оси, проходящей через центр масс (т — масса, R — радиус шара).

Момент инерции — скалярная физическая величина, мера инертности тела во вращательном движении вокруг оси, подобно тому, как масса тела является мерой его инертности в поступательном движении. Характеризуется распределением масс в теле: момент инерции относительно некоторой оси равен сумме произведений элементарных масс на квадрат расстояний до этой оси. Моменты инерций однородных тел простейшей формы легко выражаются через массу и геометрические характеристики.

Второй закон Ньютона для вращательного движения имеет вид:

,

где L – момент импульса тела, величина равная произведению момента инерции тела на угловую скорость , M – момент сил

Моменты инерции однородных тел простейшей формы относительно некоторых осей

Тело	Положение оси a	Момент инерции Ja
Полый тонкостенный цилиндр (кольцо) радиуса R и массы m	Ось цилиндра
Сплошной цилиндр (диск) радиуса R и массы m	Ось цилиндра
Конус радиуса R и массы m	Ось конуса
Шар радиуса R и массы m	Ось проходит через центр шара
Тонкостенная сфера радиуса R и массы m	Ось проходит через центр сферы
Прямой тонкий стержень длины l и массы m	Ось перпендикулярна к стержню и проходит через его середину
Прямой тонкий стержень длины l и массы m	Ось перпендикулярна к стержню и проходит через его конец

Т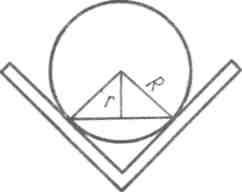 ак как шар катится по желобу прямоугольного сечения, его угловую скорость следует вычислять по фор­муле (рис. 1).

Из рисунка видно, что при ,

, т.е. рис.1

Следовательно, первое равенство можно записать в виде:

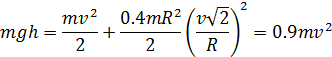
Откуда

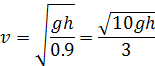
Поскольку скорость шара в любой момент времени пропорцио­нальна корню квадратному из высоты h, движение шара — равно­ускоренное.