Изучение основного уравнения динамики вращательного движения

Цель работы: Исследуйте зависимость углового ускорения диска от момента силы упругости нити, приводящего диск во вращение.

Оборудование: диск на оси из набора для изучения вращательного движения с двумя шкивами разного диаметра; блок; штатив; штангенциркуль; набор грузов; нить; секундомер.

Теоретические основы работы

Угловое ускорение вращающегося тела ε прямо пропорцио­нально моменту сил М, под действием которого тело получает угловое ускорение:

Величина I, зависящая от свойств самого тела, называется моментом инерции.

Момент инерции — скалярная физическая величина, мера инертности тела во вращательном движении вокруг оси, подобно тому, как масса тела является мерой его инертности в поступательном движении. Характеризуется распределением масс в теле: момент инерции относительно некоторой оси равен сумме произведений элементарных масс на квадрат расстояний до этой оси. Моменты инерций однородных тел простейшей формы легко выражаются через массу и геометрические характеристики.

Моменты инерции однородных тел простейшей формы относительно некоторых осей

Тело	Положение оси a	Момент инерции Ja
Полый тонкостенный цилиндр (кольцо) радиуса R и массы m	Ось цилиндра
Сплошной цилиндр (диск) радиуса R и массы m	Ось цилиндра
Конус радиуса R и массы m	Ось конуса
Шар радиуса R и массы m	Ось проходит через центр шара
Тонкостенная сфера радиуса R и массы m	Ось проходит через центр сферы
Прямой тонкий стержень длины l и массы m	Ось перпендикулярна к стержню и проходит через его середину
Прямой тонкий стержень длины l и массы m	Ось перпендикулярна к стержню и проходит через его конец

Для проверки этого уравнения, называемого основным урав­нением динамики вращательного движения твердого тела, вос­пользуемся установкой, изображенной на рисунке 1.

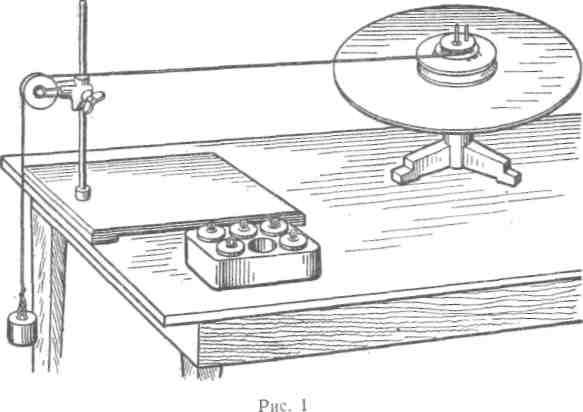
На один из шкивов радиусом R намотаем нить. Нить пере­кинем через блок и к концу ее подвесим груз массой т.

Момент М силы упругости F нити равен .

Модуль F силы упругости нити можно определить, применив для груза второй закон Ньютона:

.

В условиях работы ускорение а груза намного меньше ускорения свободного падения g (a << g). Следовательно, можно считать, что и .

Угловое ускорение ε по определению равно:

Так как в данном опыте начальная угловая скорость ω₀ равна нулю, то

где ω₀ – угловая скорость вращения диска, которую он приобрета­ет за время t падения груза.

Порядок выполнения работы

Задание 1. Установите зависимость углового ускоре­ния диска от действующей силы при постоянном плече этой силы.

1. Наматывая нить на верхний шкив радиусом R₁, поднимите груз массой m₁ = 0,1 кг на максимальную высоту. Отпустите груз и с помощью секундомера определите время t₁ его падения.

2. После достижения грузом поверхности пола вычислите угловую скорость диска ω_t. Для этого, пренебрегая действием сил трения, измерьте время t^’₁, необходимое для совершения диском пяти оборотов, и вычислите угловую скорость

После опускания груза на поверхность пола нить полностью должна сматываться со шкива диска.

3. Вычислите угловое ускорение ε₁:

4. Повторив опыт с грузом массой m₂ = 0,2 кг, вычислите угловую скорость ω₂ и угловое ускорение ε₂:

3. Результаты измерений и вычислений занесите в отчетную таблицу 1.

Отчетная таблица

R1, м	F1, Н	F2, H	F1/F2	t1, c	t2, c	ω1, c-1	ω2, c-1	ε1, c-2	ε2, c-2	ε1/ ε2
2.5*10-2	1	2	0,5

6. Рассчитайте границы погрешностей измерений, сравните и сделайте вывод.

Задание 2. Исследуйте зависимость углового ускорения диска от плеча действующей силы.

1. Наматывая нить на шкив радиусом R₂, поднимите груз массой m₁ = 0,1 кг; отпустив его, определите время падения груза t₃.

2. После достижения грузом поверхности пола вычислите угловую скорость вращения диска 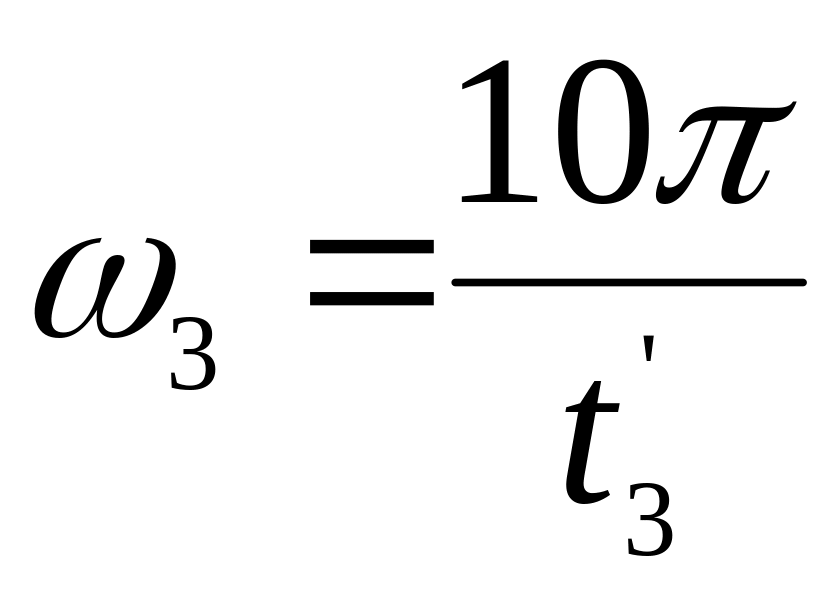и угловое ускорение

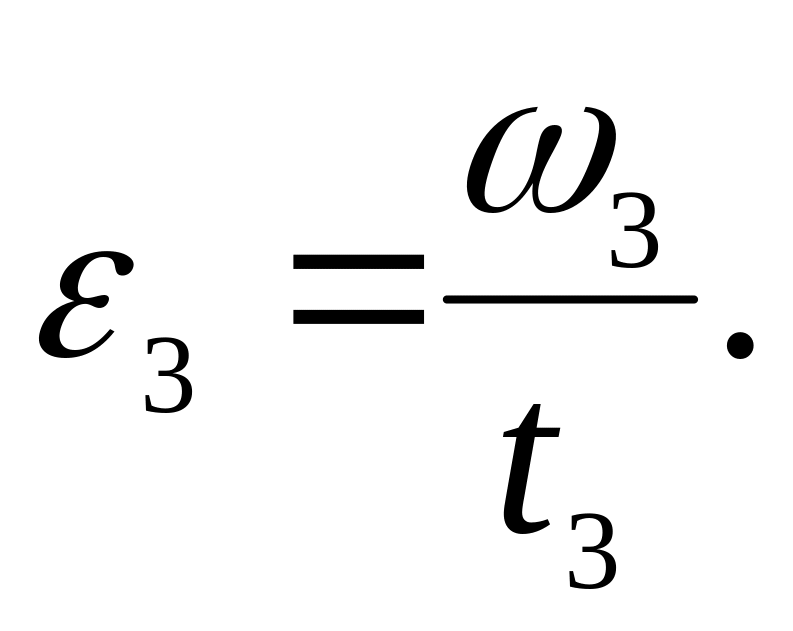
3. Сравните отношения R₁/R₂ и ε₁/ε₃, сделайте вывод. (Значения R₁ и ε₁ получены при выполнении первого задания.)

4. Результаты измерений и вычислений занесите в таблицу 2.

Отчетная таблица 2

m1, кг	R1, м	R2, м	R1/ R2	t3, c	ω3, c-1	ε3, c-2	ε1, c-2	ε1/ ε3
0.1	2.5*10-2	5*10-2	0.5

5. По результатам выполнения двух заданий сделайте общий вывод о зависимости углового ускорения диска от момента сил. Для этого сравните отношения угловых ускорений и соответст­вующих моментов сил.

Контрольные вопросы

1. Поясните принцип действия установки, с помощью кото­рой проверяют основное уравнение динамики вращательного дви­жения твердого тела.

2. Вычислите линейное ускорение движения груза и срав­ните его с ускорением свободного падения. Правильным ли было предположение, что в данной работе a << g?

3. Объясните причины неточного совпадения отношений и

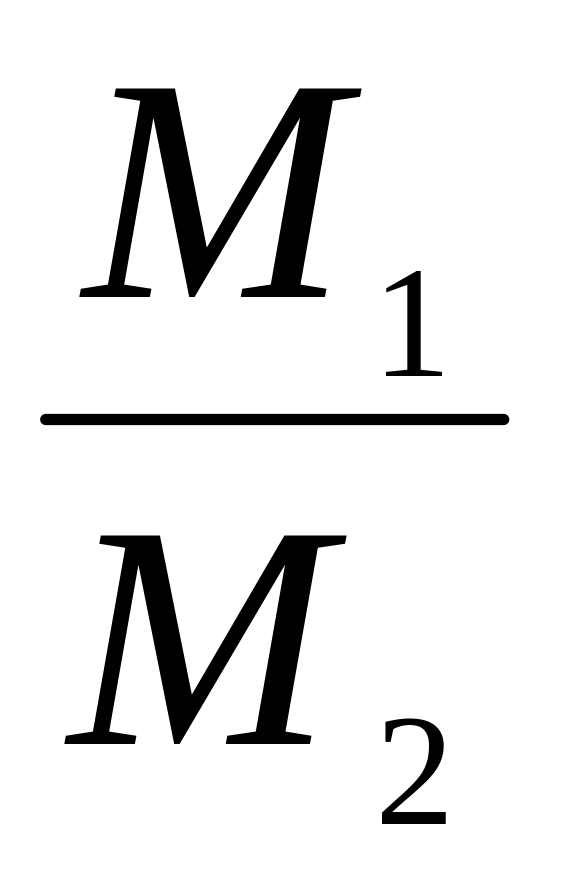
Творческий практикум

Используя данную установку, измерьте момент инерции диска

Лабораторная работа № 8

ИЗУЧЕНИЕ ДВИЖЕНИЯ ТЕЛА, БРОШЕННОГО ГОРИЗОНТАЛЬНО

Цель работы: исследование зависимости дальности полета тела, брошенного горизонтально, от высоты, с которой оно начало движение.

Оборудование: штатив с муфтой и лапкой, желоб дугообразный, шарик стальной, пленка отметчик, направляющая прибора для изучения прямолинейного движения, скотч.

Теоретические основы работы

Если тело бросить с некоторой высоты горизонтально, то его движение можно рассматривать, как движение по инерции по горизонтали и равноускоренное движение по вертикали.

По горизонтали тело движется в соответствии первым законом Ньютона, поскольку кроме силы сопротивления со стороны воздуха, которую не учитывают, в этом направлении на него никакие силы не действуют. Силой сопротивления воздуха можно пренебречь, так как за короткое время полета тела, брошенного с небольшой высоты, действие этой силы заметного влияния на движение не окажет.

По вертикали на тело действует сила тяжести, которая сообщает ему ускорение g (ускорение свободного падения).

Рассматривая перемещение тела в таких условиях как результат двух независимых движений по горизонтали и по вертикали, можно установить зависимость дальности полета тела от высоты, с которой его бросают. Если учесть, что скорость тела V в момент броска направлена горизонтально, и вертикальная составляющая начальной скорости отсутствует, то время падения можно найти, используя основное уравнение равноускоренного движения:

, откуда .

За это время тело успевает пролететь по горизонтали, двигаясь равномерно, расстояние . Подставив в эту формулу уже найденное время полета, и получают искомую зависимость дальности полета от высоты и скорости:

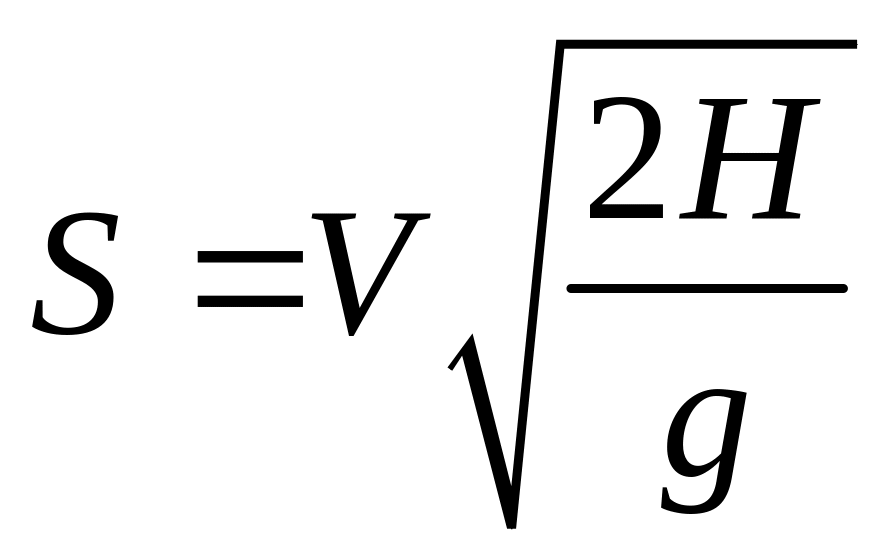(1)

Из полученной формулы видно, что дальность броска находиться в квадратичной зависимости от высоты, с которой бросают. Например, при увеличении высоты в четыре раза, дальность полета возрастет вдвое; при увеличении высоты в девять раз, дальность возрастет в три раза и т.д.

Этот вывод можно подтвердить более строго. Пусть при броске с высоты H₁ дальность составит S₁, при броске с той же скоростью с высоты H₂ = 4H₁ дальность составит S₂.

По формуле (1):

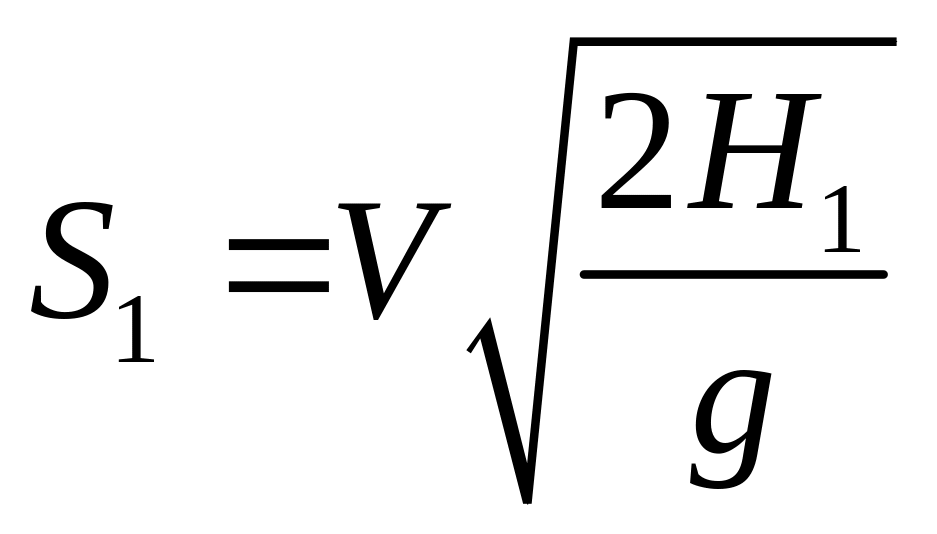, и

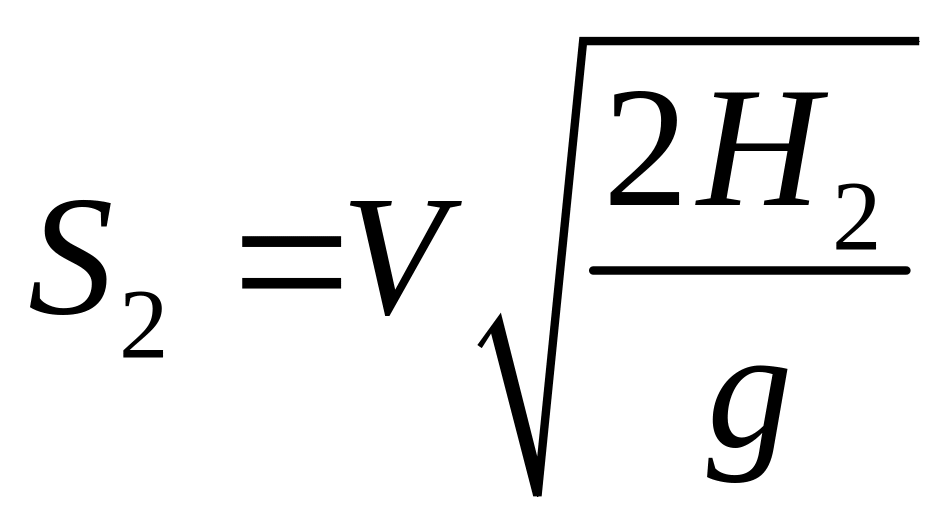
Тогда поделив второе равенство на первое получим:

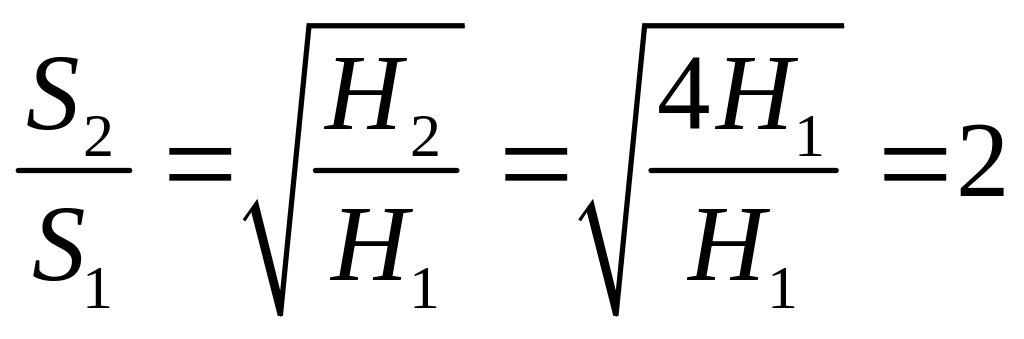или (2)

Эту зависимость, полученную теоретическим путем из уравнений равномерного и равноускоренного движения, в работе проверяют экспериментально.

В работе исследуется движение шарика, который скатывается с желоба. Желоб закреплен на некоторой высоте над столом. Это обеспечивает горизонтальное направление скорости шарика в момент начала его свободного полета.

Проводят две серии опытов, в которых высоты горизонтального участка желоба отличаются в четыре раза, и измеряют расстояния S₁ и S₂, но которые удаляется шарик от желоба по горизонтали. Для уменьшения влияния на результат побочных факторов определяют среднее значение расстояний S_1ср и S_2ср. Сравнивая средние расстояния, полученные в каждой серии опытов, делают вывод о том, насколько справедливо равенство (2).