Порядок выполнения работы

1. Надев нитяную или проволочную петлю на штифты грузов, установите их симметрично относительно оси вращения. Измерьте расстояние r₁ от оси до центра масс каждого из грузов.

2. Приведите систему во вращение, удерживая петлей грузы на расстоянии r₁ от оси вращения, и измерьте время t₁, необходи­мое для совершения системой пяти оборотов.

3. Сдерните петлю и измерьте новое время t₂, необходимое для совершения системой пяти оборотов.

4. Измерьте расстояние r₂ от центра масс каждого груза до оси вращения.

5. Повторите опыт еще 2 раза. Результаты измерений и вы­числений занесите в отчетную таблицу.

Отчетная таблица

№ опыта	r1, м	r2, м	t1, с	t2, с
1
2
3

6. Оцените границы погрешностей измерений величин и и сделайте вывод о выполнении закона сохранения момента импульса.

Контрольные вопросы

1. Поясните принцип действия установки, использованной в работе.

2. Укажите основные причины, которые приводят к погреш­ностям при выполнении этой работы, а также способы уменьшения этих погрешностей.

3. Изменяется ли кинетическая энергия вращающейся системы тел при вдергивании нити?

Лабораторная работа № 5

ИЗМЕРЕНИЕ КИНЕТИЧЕСКОЙ ЭНЕРГИИ ВРАЩАЮЩЕГОСЯ ДИСКА

Цель работы: Рассчитать кинетическую энергию диска, вращающегося с за­данной угловой скоростью ω, и сравнить с кинетической энергией вращающегося диска, полученной в результате эксперименталь­ных измерений.

Оборудование: диск на оси; два скрепленных параллельно учебных динамометра; штатив; линейка; нить; секундомер; весы; гири.

Теоретические основы работы

Кинетическая энергия вращающегося диска рассчитывается по формуле:

где I — момент инерции диска, ω — угловая скорость его вра­щения

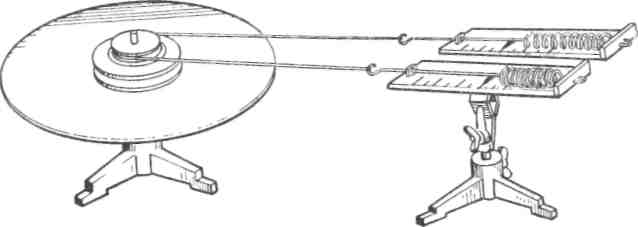
Рис. 1

Момент инерции — скалярная физическая величина, мера инертности тела во вращательном движении вокруг оси, подобно тому, как масса тела является мерой его инертности в поступательном движении. Характеризуется распределением масс в теле: момент инерции относительно некоторой оси равен сумме произведений элементарных масс на квадрат расстояний до этой оси. Моменты инерций однородных тел простейшей формы легко выражаются через массу и геометрические характеристики.

Моменты инерции однородных тел простейшей формы относительно некоторых осей

Тело	Положение оси a	Момент инерции Ja
Полый тонкостенный цилиндр (кольцо) радиуса R и массы m	Ось цилиндра
Сплошной цилиндр (диск) радиуса R и массы m	Ось цилиндра
Конус радиуса R и массы m	Ось конуса
Шар радиуса R и массы m	Ось проходит через центр шара
Тонкостенная сфера радиуса R и массы m	Ось проходит через центр сферы
Прямой тонкий стержень длины l и массы m	Ось перпендикулярна к стержню и проходит через его середину
Прямой тонкий стержень длины l и массы m	Ось перпендикулярна к стержню и проходит через его конец

Момент инерции диска равен:

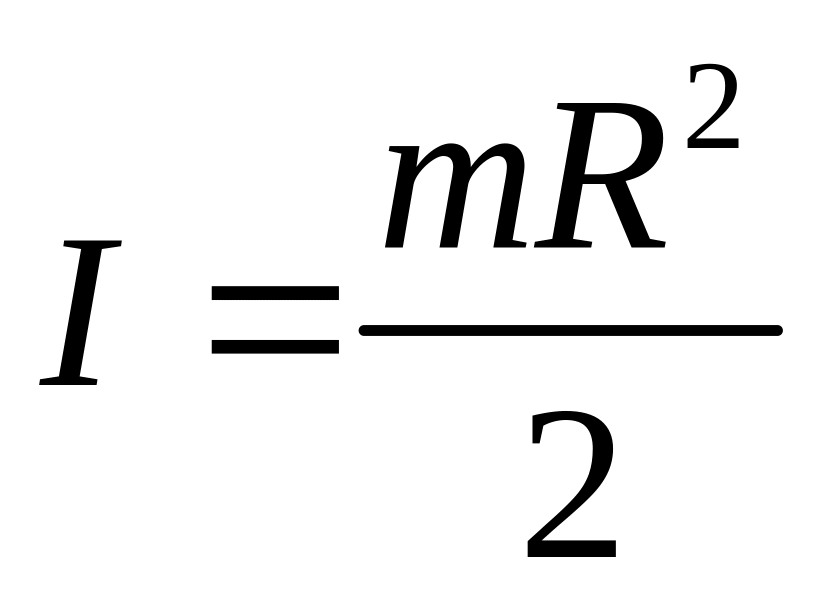, где т – масса диска, R – его радиус.

Кинетическую энергию вращающегося диска можно определить экспериментально. Для этого надо измерить работу, которая совершается при торможении диска до полной остановки:

где F_тp — сила трения, под действием которой останавливается диск, l – путь, на котором действует сила трения. В данной работе торможение диска осуществляется с помощью нити, перекинутой через шкив диска. Концы нити прикреплены к двум динамометрам, расположенным горизонтально (рис. 1).

Вследствие трения нити о шкив диска динамометры дают раз­ные показания F₁ и F₂. Разность этих показаний равна силе трения:

Сила трения действует на пути l, равном произведению длины окружности шкива на число оборотов п, совершаемых диском при торможении до полной остановки. Тогда

(r — радиус шкива).