Творческий практикум

Две пружины с коэффициентами жесткости k₁ и k₂ соединяют один раз последовательно, а другой раз – параллельно. Какой должна быть жесткость k пружины, которой можно было бы заменить эту систему из двух пружин? Первоначальная длина пружин одинакова.

Последовательное соединение	Параллельное соединение

Лабораторная работа № 4

ИЗУЧЕНИЕ ЗАКОНА СОХРАНЕНИЯ МОМЕНТА ИМПУЛЬСА

.

Цель работы: убедиться на опыте в справедливости закона сохранения мо­мента импульса.

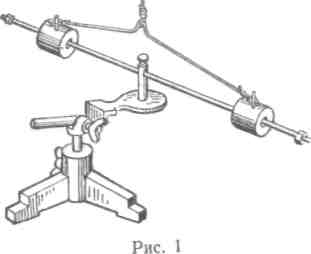
Оборудование: стержень на оси; два груза, скользящие по стержню; нить; секундомер; линейка; весы учебные; гири; проволока

Теоретические основы работы

Второй закон Ньютона для вращательного движения имеет вид:

,

где L – момент импульса тела, величина равная произведению момента инерции тела угловую скорость , M – момент сил.

Момент инерции — скалярная физическая величина, мера инертности тела во вращательном движении вокруг оси, подобно тому, как масса тела является мерой его инертности в поступательном движении. Характеризуется распределением масс в теле: момент инерции относительно некоторой оси равен сумме произведений элементарных масс на квадрат расстояний до этой оси. Моменты инерций однородных тел простейшей формы легко выражаются через массу и геометрические характеристики.

Моменты инерции однородных тел простейшей формы относительно некоторых осей

Тело	Положение оси a	Момент инерции Ja
Полый тонкостенный цилиндр (кольцо) радиуса R и массы m	Ось цилиндра
Сплошной цилиндр (диск) радиуса R и массы m	Ось цилиндра
Конус радиуса R и массы m	Ось конуса
Шар радиуса R и массы m	Ось проходит через центр шара
Тонкостенная сфера радиуса R и массы m	Ось проходит через центр сферы
Прямой тонкий стержень длины l и массы m	Ось перпендикулярна к стержню и проходит через его середину
Прямой тонкий стержень длины l и массы m	Ось перпендикулярна к стержню и проходит через его конец

При вращении тела вокруг оси момент импульса тела L со­храняется, если момент М внешних сил относительно этой оси равен нулю:

, если M= 0.

Для проверки этого закона применяется установка, изобра­женная на рисунке 1.

На легкий стержень, который с малым трением может вращать­ся вокруг вертикальной оси, на одинаковом расстоянии от оси вращения надеты два груза рав­ной массы. Грузы удерживают­ся на заданном расстоянии нитя­ной или проволочной петлей. Если привести стержень с груза­ми во вращение с угловой ско­ростью ω₁, то приобретенный мо­мент импульса системы будет определяться выражением:

,

где – момент инерции груза относительно оси враще­ния (т — масса груза, r₁ — расстояние от оси вращения до центра масс каждого из грузов), — момент инерции стержня относительно оси, проходящей через его середину (т_с — масса стержня, l — его длина).

В данной установке массы стержня и грузов подобраны так, чтобы моментом инерции стержня по сравнению с моментом инерции грузов можно было пренебречь. В этом случае .

Угловую скорость вращения системы ω₁ определим, зная время t₁, необходимое для совершения грузами пяти оборотов:

(n=5 об).

При сдергивании нитяной или проволочной петли, удержи­вающей грузы, момент инерции системы тел увеличивается за счет того, что грузы расходятся до концов стержня. Угловая скорость системы при этом уменьшается.

Момент импульса системы L₂ можно определить, как и в первом случае, по формуле:

.

Сравнивая значения величин L₁ и L₂, можно эксперимен­тально проверить закон сохранения момента импульса. Из равенства L₁=L₂ следует:

, .

Так как и , то получим, что , или .

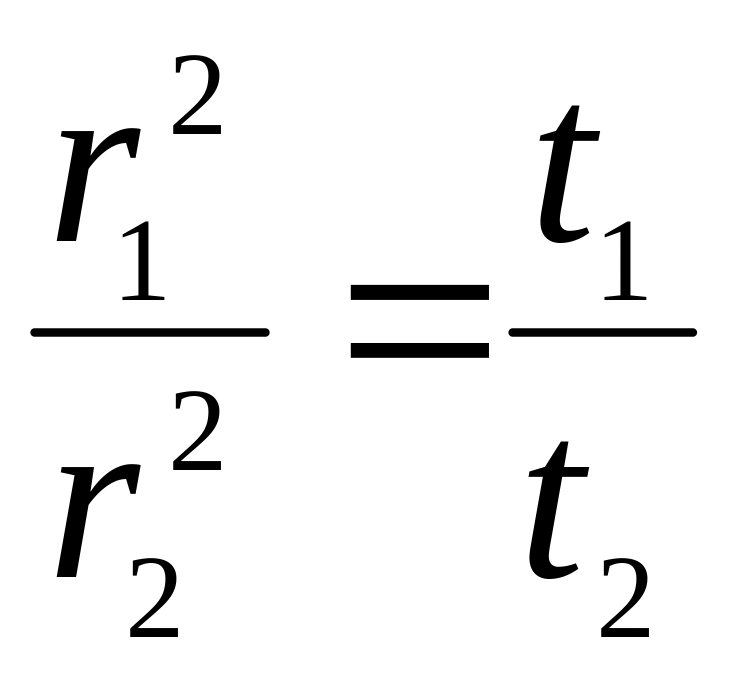Таким образом, для проверки закона сохранения момента импульса достаточно проверить выполнение равенства

где t₁ и t₂— время, необходимое для совершения одинакового числа оборотов стержнем до и после сдергивания петли.