33. Свойства неопределенного интеграла интегралы от основных элементарных ф-ий.

Произв. от неопр. интеграла равна подинтегр. ф-ии.

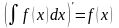
Диференциал неопр. интеграла равен подинтегр. выражению

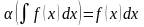
Неопред. интеграл от диференциала некотор. ф-ии равен этой ф-ии с точностью до постоянного слогаемого

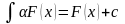
Постоянный множитель можно выносить за знак интеграла.

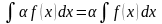
Интеграл от алгебраической суммы функций равен такой же сумме интегралов от этих ф-ий.

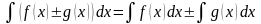
Табличные интегралы

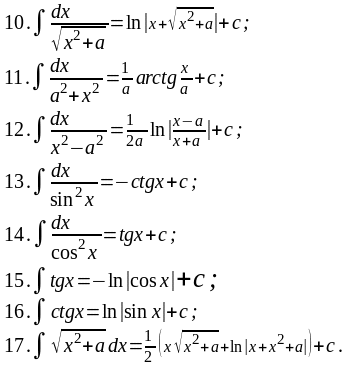
35. Метод интегрирования по частям. Если и=φ₁(х), v=φ₂(х) – диференциальн. ф-ии, то из формулы диференциала произведения двух ф-ий d(u∙v)^/ = udv + vdv получается формула интегрирования по частям

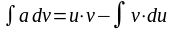
Эта формула применяется в случае, когда подинтегральная ф-ия представляет собой произведение алгебраической ф-ии и трансцендентной.

В качестве и, обычно, выбирается ф-ия, которая упрощается дифференцированием, а в качестве dv оставшаяся часть подинтнгрального выражения, содержащая dx, из которой можно определить v, путём интегрирования.

37. Св-ва опр.интеграла

1) Постоянный множитель можно вынести за знак интеграла: = .

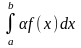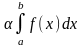2) Интеграл от алгебр. суммы ф-ций равен такой же сумме интегралов:

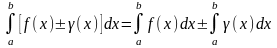
3) Если отрезок интегрирования разбить на части, то интеграл на всём отрезке равен сумме интегралов для каждой из возможных частей: .

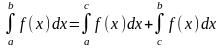4) Если на отрезке [a;b], где a<b заданы ф-ции f(x)dx=y(x), то обе рав-ва можно почленно интегрировать:

.

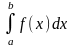
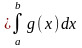26. Возрастание убывание функции. Если дифференцируемая на интервале (a;b) функция ƒ(х) возрастает (убывает), то ƒ'(х)≥0 (ƒ"(х)≤0) для любого x є (a;b). Теорема 25.7 (достаточные условия). Если функция ƒ(х) дифференцируема на интервале (a;b) и ƒ'(х)>0 (ƒ'(х)<0) для любого xє(a;b), то эта функция возрастает (убывает) на интервале (a;b).

28.

.

30. Ассимптота

Прямая называется асимптотой графика функции y = f(x), если расстояние от переменной точки M графика до этой прямой при удалении точки M в бесконечность стремится к нулю, т.е. точка графика функции при своем стремлении в бесконечность должна неограниченно приближаться к асимптоте.

Кривая может приближаться к своей асимптоте, оставаясь с одной стороны от нее или с разных сторон, бесконечное множество раз пересекая асимптоту и переходя с одной ее стороны на другую.

Если обозначим через d расстояние от точки M кривой до асимптоты, то ясно, что d стремится к нулю при удалении точки M в бесконечность.

24. Производные высших порядков Производная у'=ƒ'(х) функции у=ƒ(х) есть также функция от х и называется производной первого порядка.

Если функция ƒ'(х) дифференцируема, то ее производная называется производной второго порядка и обозначается у"

Итак, у"=(у')'.

Производная от производной второго порядка, если она существует, называется производной третьего порядка и обозначается у'" (или ƒ'"(х)). Итак, у'"=(y")'

Производной n-го порядка (или n-й производной) называется производная от производной  (n-1) порядка:

y(n)=(y(n-1))¢ .

Производные порядка выше первого называются производными высших порядков.

Начиная с производной четвертого порядка, производные обозначают римскими цифрами или числами в скобках (уν или у(5)— производная пятого порядка).