22. Кинематика планетарной передачи

Планетарные механизмы получаются из дифференциальных путём закрепления одного из центральных колёс.

Д 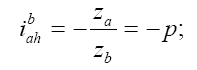ля передачи, изображенной на рис. 1.1., имеем: передаточное отношение при

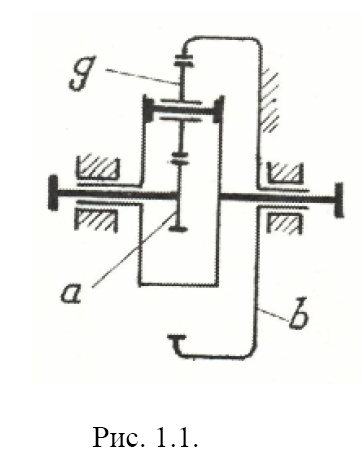
передаточное отношение планетарной передачи :

у гловые скорости звеньев:

Планетарные механизмы применяют для получения больших передаточных отношений.

Р ассмотрим другой вид планетарной передачи: Для передачи, приведенной на рис. 1.2, имеем передаточное отношение при :

передаточное отношение планетарной передачи:

угловые скорости звеньев:

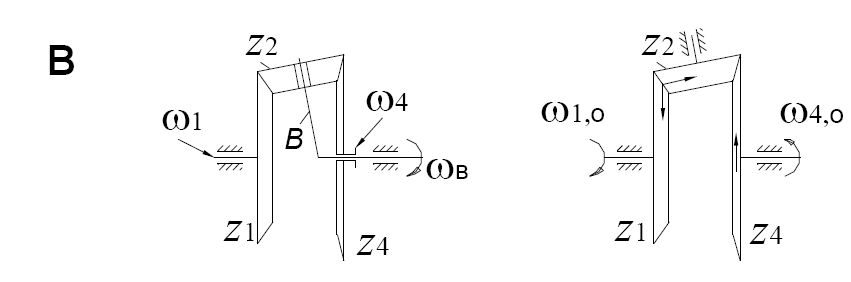
23. Кинематика дифференциального механизма

Н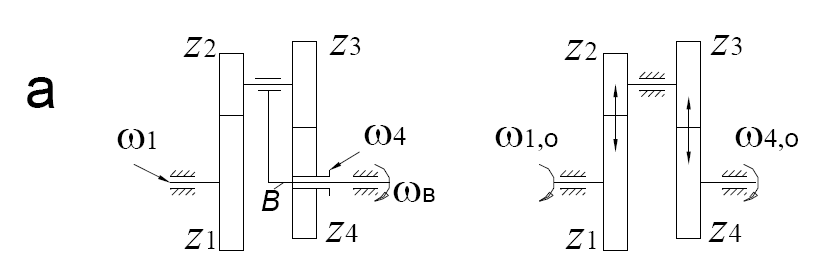 а рис. 4 показаны дифференциальные механизмы: а, б – с цилиндрическими колесами, в, г – с коническими колесами. Последний дифференциальный механизм называют коническим дифференциалом. В этих механизмах должны быть заданы два независимых движения, чтобы третье движение было определенным, например, ω1 и ω2 – заданные движения ведущих звеньев, ωВ – зависимое движение ведомого звена – водила. Определение угловой скорости ведомого звена при заданных движениях ведущих звеньев производят обычно с помощью обращенного движения. Сущность этого способа заключается в следующем. 1. Дадим всему механизму угловую скорость, равную скорости водила, но противоположно направленную (–ωВ). Получим обращенный механизм. На рис. 4 рядом с дифференциальными механизмами справа показаны их обращенные механизмы, для которых:

ω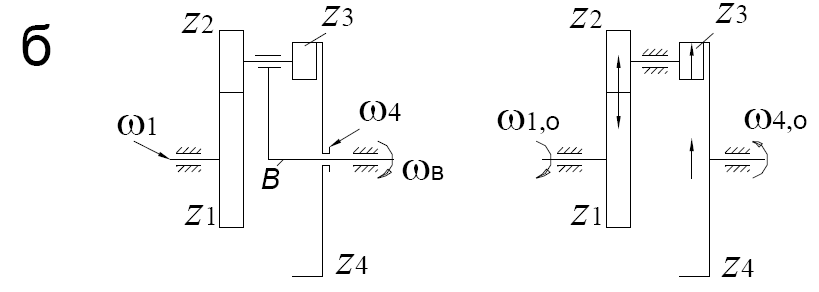 1,о = ω1 – ωв, ωв,о = ωв – ωв =0,

ω4,о = ω4 – ωв, т. е. в обращенном механизме водило неподвижно (и не изображается). Здесь ω1,О , ωВ,О , ω4,О – скорости звеньев обращенного механизма. 2. Для обращенного механизма определим передаточное отношение между двумя звеньями: первым и последним, в данных механизмах – четвертым.

П ередаточное отношение обращенного механизма будем помечать дополни-

т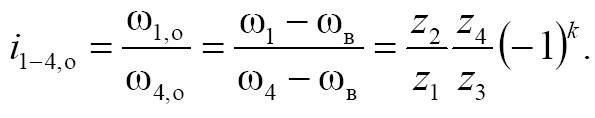 ельным индексом «о». С учетом (1) запишем

В этом выражении показатель степени «k» определяет знак передаточного

отношения i1-4,о , который необходимо учитывать. На рис. 4а звенья 1 и 4 в об-

ращенном механизме вращаются в одну сторону, k = 2, передаточное отношение считается положительным. На рис. 4б звенья 1 и 4 вращаются в разные стороны, k = 1 и передаточное отношение считается отрицательным. Направление движения звеньев в обращенных механизмах определяется по «правилу стрелок». Стрелки на колесах показывают направление перемещения расположенных ближе к наблюдателю зубьев колес. Для цилиндрических дифференциальных механизмов показатель степени «k» можно считать равным числу внешних зацеплений, поскольку внешнее зацепление изменяет направление вращения, тогда как внутреннее – не изменяет (рис. 1). Из выражения (2) определяется неизвестное движение дифференциального механизма ωВ.

Аналогично определяется скорость ω4 при заданных ω1, ωВ и скорость

ω1 – при заданных ω4, ωВ. Следует помнить, что заданные угловые скорости

подставляются в выражение (2) со своими знаками. Для конического дифференциала (рис. 4г) выполняется следующее конструктивное условие: z1 = z4, z2 = z3. Колесо z3 необходимо здесь для уравновешивания вращающихся масс и разгрузки валов и опор от сосредоточенных сил. Выражение (2) преобразуется в следующее:

Полученная формула показывает, что конический дифференциал позволяет механически производить операцию сложения или вычитания скоростей.