7.Применение и использование закона сохранения импульса. Закон сохранения энергии.
Законы сохранения импульса и момента импульса выполняются при любом взаимодействии, об этом свидетельствуют многочисленные экспериментальные данные. Таким образом, эти законы справедливы в мега-, макро- и микромире, и называются великими законами сохранения.
В мега мире закон сохранения момента импульса объясняет наблюдаемую форму галактик. Каждая галактика образовывалась из очень большой массы газа (порядка 1039-1040 кг), обладающей первоначальным моментом импульса.
Широкое применение в современной технике имеет гироскоп. Гироскоп - это осе симметричное тело, быстро вращающееся вокруг своей геометрической оси. Простейшим примером этого прибора служит знакомая всем еще с детства игрушка - волчок. Ось вращения сохраняет свое направления в пространстве неизменным, если для удержания гироскопа использовать так называемый карданов подвес. Такие устройства нашли широкое применение в авиации и космонавтике, в устройствах, обеспечивающих ориентацию судов вблизи магнитного поля Земли.
При выборе огнестрельного оружия предпочтение отдается нарезному по сравнению с гладкоствольным. Нарезное оружие, как известно, стреляет на большие расстояния и с большей точностью. Проходя через ствол, пуля закручивается и приобретает момент импульса, направленный вдоль скорости ее движения. Этот момент импульса придает пуле устойчивую ориентацию в пространстве, так, что различные турбулентности воздуха, возникающие в силу быстрого ее движения, не могут отклонить ее от цели.
Из опытных данных хорошо известно, что элементарные частицы обладают внутренним моментом импульса.
Экспериментальные методы исследования элементарных частиц основаны на законе сохранения импульса. При столкновении элементарные частицы оставляют видимые следы (треки) в специальных камерах, заполненных перенасыщенными парами воды или перегретой жидкостью. При этом выводы о массе и свойствах элементарных частиц делаются на основании закона сохранения импульса.
В игре «бильярд» сталкиваются шарики с равной массой. Как можно заметить из опыта или заключить из закона сохранения импульса, при столкновении двух шариков с равной массой, один из которых покоился, движущийся шарик при столкновении передаст часть или весь свой импульс покоящемуся, а сам замедлит или остановит свое движение. При столкновении шариков с существенно разными массами направление и скорость движения изменит только легкий шарик. По этой причине во многих видах спорта участников соревнований делят на группы с примерно одинаковой массой участников в каждой из них.
Любое движение материальных тел осуществляется в строгом соответствии с законом сохранения импульса. Поэтому освоение околоземного пространства и полеты в космос невозможны без применения реактивной тяги.
Закон сохранения энергии.
В ньютоновской механике формулируется частный случай закона сохранения энергии — Закон сохранения механической энергии, звучащий следующим образом.
Полная механическая энергия замкнутой системы тел, между которыми действуют только консервативные силы, остаётся постоянной.
Проще говоря, при отсутствии диссипативных сил (например, сил трения) механическая энергия не возникает из ничего и не может исчезнуть в никуда.
Диссипати́вные си́лы — силы, при действии которых на механическую систему её полная механическая энергия убывает (то есть диссипирует), переходя в другие, немеханические формы энергии, например, в теплоту.
8. Применение ЗСИ и ЗСЭ к абсолютно упругому и абсолютно неупругому удару.
В тетрадке.
9.Динамика вращательно движения. Момент инерции материальной точки. Момент инерции тела
Динамические величины, характеризующие вращательные движения, различны для точек, находящихся на разных расстояниях от оси вращения. Поэтому при описании вращательного движения мы не можем использовать понятие силы, а должны использовать понятие момента силы. Вместо импульса следует применять момент импульса, вместо массы – момент инерции.
Моментом силы 
называется
произведение силы 
,
под действием которой тело вращается
на плечо силы 
.
Плечо силы – кратчайшее расстояние от оси вращения до линии действия силы. Вектор момента силы М в общем случае равен векторному произведению
. (1.43)
Момент силы является
аксиальным вектором. Если в правой
декартовой системе координат 
направить
вдоль оси 
,
а 
–
вдоль 
,
то
будет
направлен в положительном направлении
оси 
.
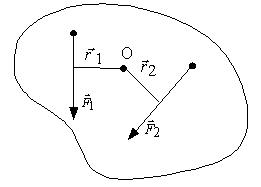
Рис. 1.13. Моменты сил М1 и M2, действующие на тело, закрепленное на оси О
Если на
тело действуют несколько сил, то для
каждой силы существует свой момент
сил 
и 
(рис.
1.13).
Действующие на тело
силы 
, и 
не
вызывают вращения, если их
моменты
и
взаимно
уравновешиваются, т. е. равны по величине
и обратны по знаку.
Момент инерции материальной
точки обозначается 
и
равен произведению массы точки
на
расстояние
от
оси вращения до точки
. (1.44)
Если тело массивное (не
является материальной точкой), то
необходимо разбить тело на маленькие
участки с массой 
,
находящиеся на расстоянии 
от
оси, и найти для каждой области свой
момент инерции
.
Результирующий момент инерции тела будет равен сумме всех моментов
. (1.45)
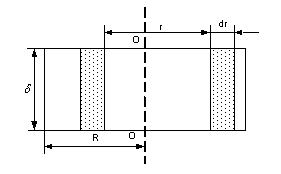
Рис. 1.14. Вычисление момента инерции однородного диска
Выражение (1.45) используется для вычисления момента инерции достаточно простых тел – диска, стержня, шара и т. д.
Пример 1. Вычислить момент инерции однородного диска толщиной д, радиусом R и плотностью с (рис. 1.14). За элементарную массу бесконечно тонкого цилиндра радиусом r, толщиной dr и высотой д примем
.
Тогда момент инерции диска
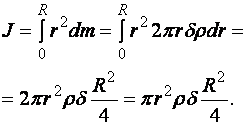
Учитывая, что масса всего диска
,
получим
.
Итак, момент инерции – это аналог массы и является мерой инерции вращающегося тела. Однако масса тела не зависит от характера движения, а значение момента инерции зависит от того, относительно какой оси он вычисляется.
Если известен момент инерции тела относительно какой-либо оси О (рис. 1.15), то момент инерции относительно параллельной оси, отстоящей от первой на расстоянии R, можно вычислить, используя теорему Штейнера:
.
Пример 2. Момент инерции диска относительно оси, проходящей по краю диска (рис. 1.15),
.
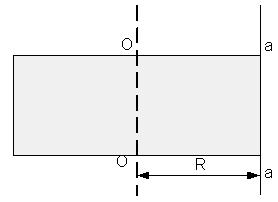
Рис. 1.15. К теореме Штейнера