1.2.2. Радиочастотный квадратурный аокпи

В традиционной радиоэлектронике известен и применяется метод корреляционной обработки радиосигналов, при котором осуществляется перенос спектра входного сигнала в область нулевой частоты. Это влечет за собой необходимость введения дополнительного квадратурного канала обработки, так как в противном случае выходной сигнал коррелятора будет зависеть от начальной фазы обрабатываемого колебания.

Описанная процедура обработки эффективно реализуется в акустооптическом варианте на основе двумерного опорного транспаранта (рис.1.16).

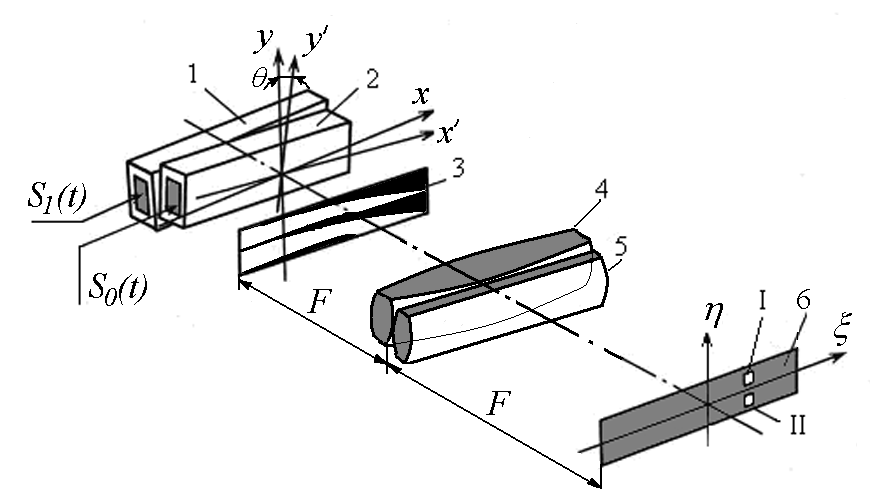
Рис. 1.16. Квадратурный АОКПИ для радиосигналов

Схема процессора представляет собой двухканальный АОКПИ, построенный на основе двумерного опорного транспарата. На вход сигнального АОМ 1 поступает произвольный радиосигнал , где , и – законы его амплитудной, фазовой модуляции и начальная фаза соответственно. Опорный сигнал формируется при помощи двумерного опорного транспарата в составе АОМ 2 и кодирующего транспаранта 3. Опорный АОМ 2 ориентирован по отношению к АОМ 1 под углом θ, как показано на рис.1.16, и возбуждается гармоническим колебанием . Для преобразования дифракционного светового поля в плоскость расположения фотоприемника используется астигматическая пара линз (совокупность сферической 4 и цилиндрической 5 линз, каждая из которых имеет фокусное расстояние F). Структура опорного транспаранта 3 представлена на рис. 1.16. Она состоит из двух одинаковых транспарантов высотой каждый, разнесенных вдоль координаты у. Форма окон прозрачности задается введенными выше функциями и с той лишь разницей, что появляются постоянные смещения и соответственно в I и II каналах (см. рис. 1.17,а).

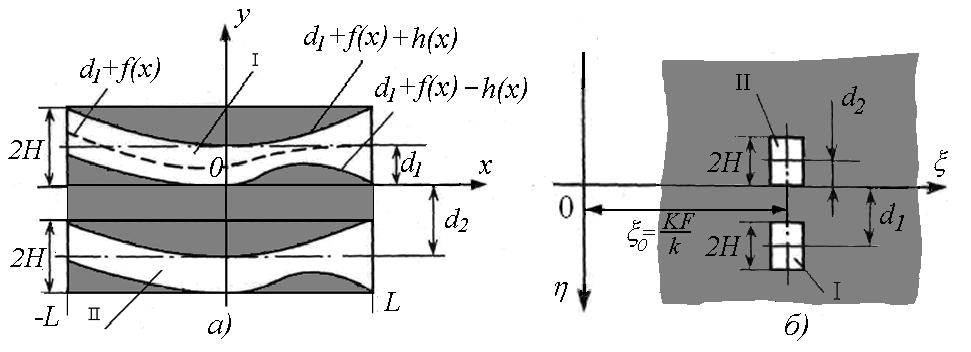
Рис. 1.17. Кодирующий транспарант в радиочастотном квадратурном АОКПИ

Транспарант фактически расположен в выходной плоскости АОМ 2, смещение вдоль оптической оси показано для наглядности. Астигматическая пара линз 4, 5 имеет фокусное расстояние в вертикальной плоскости , а в горизонтальной — , поэтому в плоскости вдоль оси осуществляется преобразование Фурье, тогда как вдоль оси строится перевернутое изображение выходной апертуры КТ в масштабе 1:1.

Размещение областей прозрачности фокальной диафрагмы 6 вдоль оси (рис. 1.17,б) адекватно структуре транспаранта вдоль оси , а их расположение вдоль оси совпадает с локализацией одного из первых порядков дифракционной картины. Два фотодетектора, чувствительные площадки которых расположены непосредственно за отверстиями I и II диафрагмы 6, на схеме не показаны.

Структура обоих каналов полностью совпадает, а их единственное отличие, состоит в пространственном разносе вдоль вертикальной оси, вследствие которого оказываются различными начальные фазы гармонического колебания (которое выполняет функцию динамического несущего транспаранта) в апертурах КТ обоих каналов. Это обстоятельство и позволяет организовать квадратурную корреляционную обработку радиосигналов.

Проведем формальный анализ работы процессора, для этого достаточно найти выходной сигнал одного (например, первого канала). Принимая во внимание, что в процессоре реализуется механизм параллельной дифракции, запишем световое поле, дифрагировавшее в направлении +1 порядка на сигнале и на двумерном опорном транспаранте:

,

где  комплексная огибающая входного сигнала, считается, что для динамического НТ , и − постоянные коэффициенты, фактические значения которых для рассматриваемого вопроса несущественны и в дальнейшем будут изменяться. Астигматическая пара линз в плоскости фотоприемника формирует световое поле:

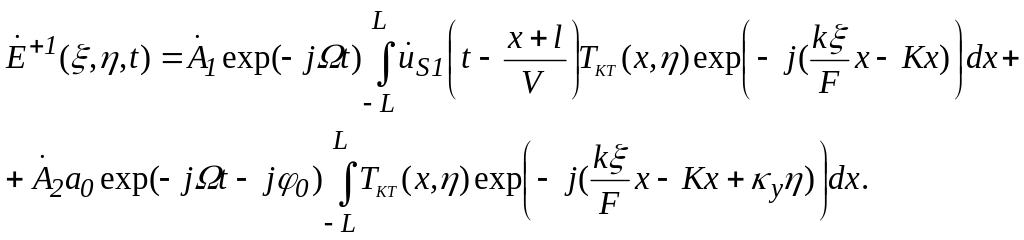
Интенсивность светового поля в области +1 дифракционного можно представить в виде:

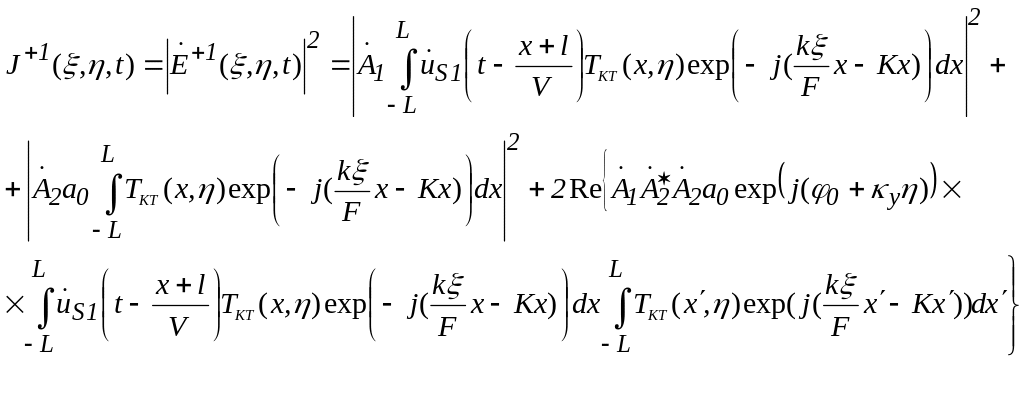. (1.26)

Согласно (1.26) интенсивность содержит три слагаемых: первое обусловлено дифракцией света на сигнале , второе−дифракцией на опорном гармоническом колебании , третье−интерференцией этих световых полей. Практически всегда уровень обрабатываемого сигнала значительно меньше уровня опорного колебания , поэтому в выражении (1.26) первое слагаемое можно в дальнейшем опустить.

Последующие выкладки повторяют преобразования, проведенные в отношении АОСФ. Ток ФП находится усреднением интенсивности света по площади фотокатода, причем пределы интегрирования определяются согласно рис.1.17б:

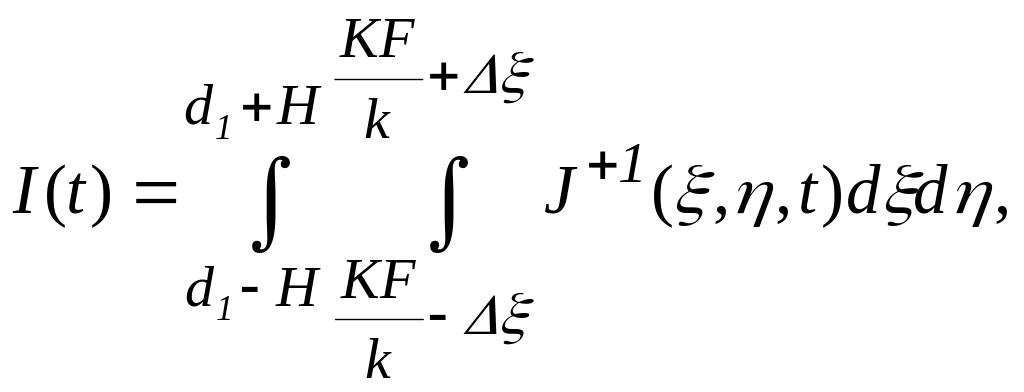(1.27)

где − физический размер окна диафрагмы (а также фотокатода) по оси . Будем считать размеры ФП вдоль оси такими, что световое распределение по координате полностью попадает на фотокатод (формально это означает ), и можно перейти в (1.27) при интегрировании по к бесконечным пределам. После подстановки выражения для интенсивности (1.26) в (1.27) получим выходной ток ФП в виде суммы двух слагаемых, соответствующих сохраненным слагаемым интенсивности. Первое из оставшихся слагаемых дает постоянную составляющую тока и не представляют интереса. Второе слагаемое, зависящее от времени, оказывается равным

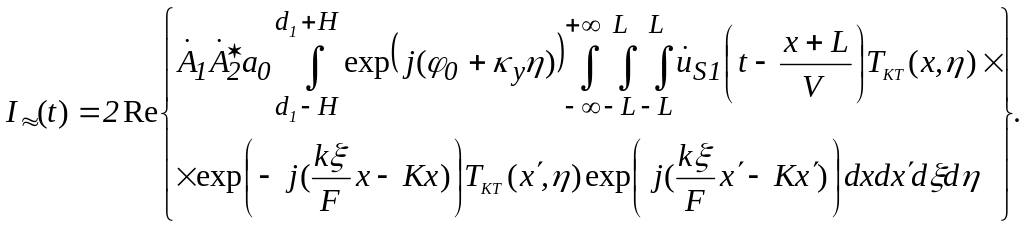(1.28)

Выражение (1.28) преобразуется следующим образом. Выделив и вычислив квадратуру по переменной , получим . Затем, используя фильтрующее свойство δ-функции, вычисляем квадратуру по , после чего получаем:

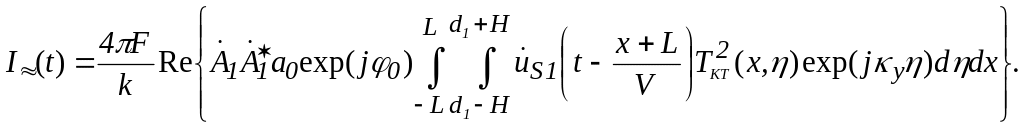(1.29)

На основании определения (1.20) функции передачи КТ выражение (1.29) преобразуется:

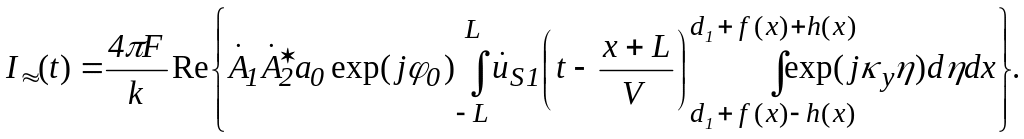(1.30)

После вычисления квадратуры по η получим информативную составляющую тока ФП:

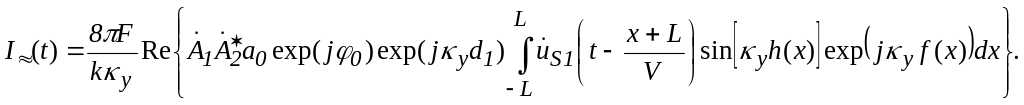
(1.31)

Замечаем, что интеграл в выражения (1.31) представляет собой свертку сигнала и импульсной реакции двумерного опорного транспаранта (см. формулу (1.25)). Остается преобразовать (1.31) к виду, явно содержащему ВКФ пары сигналов. Для этого определим радиосигнал , соответствующий импульсной реакции ОТ, и его комплексную огибающую . В формуле (1.31) сделаем замену переменных , получим

.

Зададим амплитудную и фазовую функции сигнала следующим образом:

Эти функции определяют комплексную огибающую сигнала :

.

Наконец, введя новую переменную , приходим к конечному выражению для информативной составляющей тока первого канала, которую обозначим через :

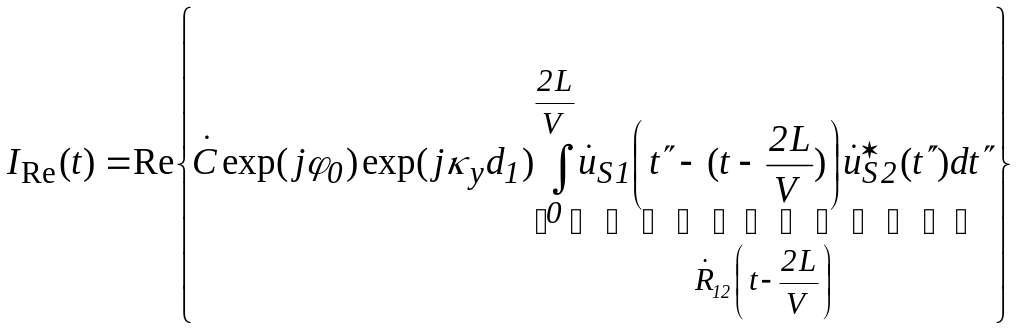, (1.32)

где − новый коэффициент пропорциональности, а квадратура является комплексной огибающей ВКФ сигналов и . Таким образом, в первом канале процессора формируется вещественная часть комплексной огибающей ВКФ, умноженной на фазовый множитель с неизвестной начальной фазой . Для исключения неизвестной фазы необходимо иметь квадратурный канал, в котором формируется мнимая часть комплексной огибающей ВКФ, умноженной на тот же фазовый множитель. С этой целью используется канал II процессора. Поскольку канал II за исключением пространственного расположения тождественен каналу I, информативная составляяющая тока на его выходе находится из выражения (1.32) простой заменой :

. (1.33)

Если путем выбора расстояний и обеспечить соотношение , то, как легко видеть, выражение (1.33) даст требуемую квадратуру:

. (1.34)

Очевидно, что условием справедливости (1.34) является следующая связь между и :

.

Из имеющихся вещественной и мнимой частей ВКФ нетрудно далее электронным путем сформировать ее модуль:

. (1.35)

Таким образом, рассмотренная схема реализует хорошо известный в радиоэлектронике алгоритм квадратурной корреляционной обработки радиосигналов. Основным ее достоинством является полное использование частотных возможностей фотоприемника, поскольку обработка осуществляется на видеочастоте. Это расширяет возможности АОП корреляционного типа в области обработки широкополосных сигналов в реальном времени. Дополнительным ее достоинством (в отличие от конвольвера) является инвариантность ко времени прихода сигнала, что является следствием сонаправленного распространения волн в обоих АОМ.