1.2.1. Акустооптический согласованный фильтр. Двумерный опорный транспарант

В настоящее время известны акустооптические корреляторы с пространственным интегрированием (АОКПИ) двух типов: гетеродинные и негетеродинные.

В гетеродинных АОКПИ используется параллельная дифракция света на обрабатываемом и опорном сигналах, а выходной сигнал формируется на радиочастоте. Алгоритм получения корреляционного интеграла в этом случае проиллюстрируем применительно к схеме акустооптического согласованного фильтра (АОСФ), представленного на (рис.1.10,а).

Подлежащий обработке радиосигнал возбуждает в АОМ бегущую акустическую волну, на которой дифрагирует коллимированный когерентный световой пучок. Опорный сигнал записан на статическом транспаранте T, представляющим собой амплитудную (или фазовую) дифракционную решетку, пространственный период которой изменяется по закону угловой модуляции опорного сигнала (см.(1.17)). Совокупная дифракционная картина отображается линзой Л, выполняющей пространственное преобразование Фурье, в плоскость пространственных частот P, где расположен фотоприемник и последовательно включенный с ним полосовой усилитель. На рис (1.10,б) показан в упрощенной форме ход световых лучей в режиме линейной дифракции Рамана-Ната, причем лучи, идущие симметричным образом ниже оптической оси, не показаны, цифрами отмечены номера дифракционных порядков после АОМ, транспаранта и в плоскости пространственных частот. В области +1 дифракционного порядка плоскости пространственных частот P интерферируют две световые волны, испытавшие параллельную дифракцию на сигнале в АОМ (+1,0) и на транспаранте (0,+1). Эти волны промодулированы пространственными спектрами обрабатываемого и опорного сигналов соответственно, так, что комплексная амплитуда светового поля в плоскости пространственных частот будет иметь вид суммы спектров

,

где -оператор пространственного преобразования Фурье, и -комплексные огибающие сигналов и соответственно. При записи этой формулы (и последующих) знак равенства следует понимать условно, поскольку опускаются не имеющие на данном этапе значения постоянные множители. Помимо этого за начало отсчета времени принят момент, когда передний фронт сигнала "входит" в АОМ, т.е. достигает координаты . Ток ФП пропорционален интенсивности света, усредненной по площади фотокатода:

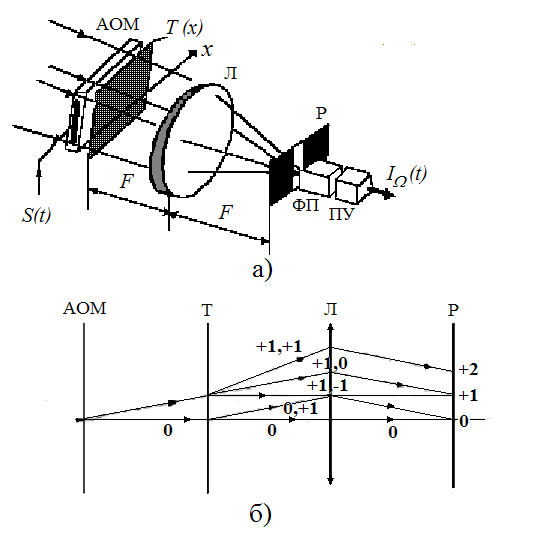
Рис. 1.10. Схема АОСФ (а) и лучевая картина дифракции (б)

_.

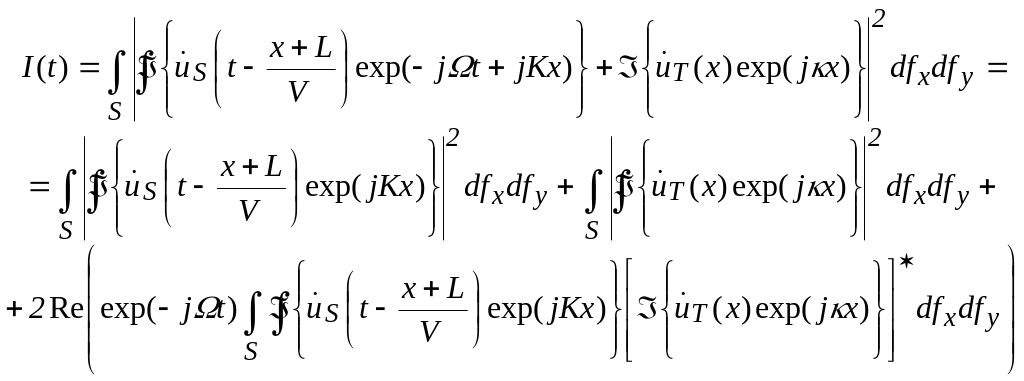Видно, что ток является суммой трех составляющих: постоянной (второе слагаемое), медленно меняющейся (первое слагаемое) и изменяющейся во времени с частотой несущего колебания сигнала (третье слагаемое). Радиочастотную составляющую можно выделить полосовым фильтром, включенным последовательно с ФП:

.

Суммарное световое распределение локализуется на его поверхности в окрестности точки , . Если размеры ФП, центр которого расположен в этой точке, достаточно велики, пределы интегрирования по , можно формально принять бесконечными, причем интегрирование по даст постоянный множитель. Будем считать, что сигнал и транспарант пространственно согласованы, т.е. период пространственной несущей транспаранта равен длине акустической волны сигнала на центральной частоте . Это означает, что . Тогда по теореме о свертке получим выражение для комплексной огибающей тока ФП

, (1.18)

которое представляет собой функцию свертки комплексных огибающих обрабатываемого и опорного сигналов, причем комплексная огибающая опорного транспаранта играет роль импульсной реакции точно так же, как в теории электрических цепей. Очевидно, что для получения взаимнокорреляционной функции сигналов достаточно изменить направление записи опорного сигнала на противоположное (т.е. просто развернуть транспарант на 180⁰ вокруг оси , тогда вместо (1.18) получаем

(1.19)

-корреляционный интеграл. При надлежащем выборе импульсной характеристики так, чтобы в момент времени выполнялось соотношение (это означает пространственное совмещение обеих комплексных огибающих) выражение (1.19) после замены переменной интегрирования преобразуется к виду

,

что представляет собой автокорреляционную функцию (АКФ) комплексной огибающей сигнала , т.е. реализуется согласованная фильтрация.

Рассмотренный АОКПИ имеет следующие п р е и м у щ е с т в а: простота корреляционной обработки широкополосных радиосигналов в реальном масштабе времени; наличие второй дополнительной пространственной координаты, позволяющей осуществлять многоканальную обработку. Главным же его н е д о с т а т к о м является трудоемкость изготовления опорных транспарантов, представляющих собой неоднородные высокочастотные дифракционные решетки. На рис.1.11 показан пример опорного транспаранта.

Рис. 1.11. Структура транспаранта с записью сигнала с бинарной

фазовой манипуляцией

Для устранения указанного недостатка в качестве опорного транспаранта может быть применена фазовая решетка, возникающая в АОМ при распространении в нем акустической волны. В результате приходим к схеме процессора, называемой конвольвером, показанной на рис.1.12.

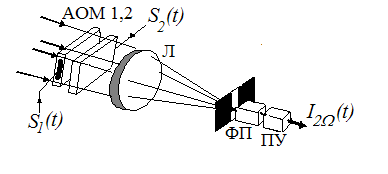
Рис. 1.12. Акустооптический конвольвер

В конвольвере выходной сигнал представляет собой радиоимпульс с удвоенной несущей частотой , что обусловлено смешением на фотокатоде двух световых волн с противоположным по знаку частотным сдвигом. Комплексная огибающая радиоимпульса есть свертка комплексных огибающих входных сигналов

.

Очевидно, что для получения корреляционной функции один из сигналов необходимо инвертировать во времени.

Конвольвер в отличие от АОСФ со статическим опорным транспарантом утрачивает присущую последнему инвариантность ко времени прихода подлежащего обработке сигнала и относится к процессорам чисто корреляционного типа.

Основное применение АОКПИ нашли при обработке радиолокационных сигналов и в системах дальней связи. Простые одномерные структуры АОКПИ имеют следующие недостатки: во-первых, ограниченная временной апертурой АОМ длительность обрабатываемых сигналов (30..50мкс при значениях несущей частоты порядка 100 МГц и единицы мкс на несущих частотах порядка 1..2 ГГц); во-вторых, сложность реализации опорных транспарантов в виде штриховых дифракционных решеток с малым (порядка длины акустической волны) переменным шагом.

Для устранения первого недостатка были разработаны двумерные АОКПИ, в которых вторая координата использовалась для размещения последовательных временных выборок обрабатываемого сигнала. Это достигалось либо применением в качестве звукопровода АОМ многозаходной линии задержки с внутренними переотражениями сигнала, либо применением внешних электрических линий задержки. Принципиально иное решение проблемы увеличения длительности обрабатываемых сигналов достигается в акустооптическом корреляторе (АОК) на основе процедуры временного интегрирования. Второй недостаток преодолевается с помощью двумерного опорного транспаранта нового типа, который существенно расширяет функциональные возможности АОКПИ.

Двумерный опорный транспарант (ОТ) базируется на идее линейно фазового транспаранта (ЛФТ), которая поясняется рис.1.13,а. Линейно-фазовый транспарант- это амплитудная (или фазовая) гармоническая дифракционная решетка, повернутая на малый угол относительно оси , перпендикулярной направлению распространения акустической волны в АОМ (т.е. оси ).

Функция прозрачности такого транспаранта, именуемого в дальнейшем несущим транспарантом (НТ), двумерна:

,

где -пространственная частота, а -пространственный период решетки. Слагаемое можно трактовать как линейно изменяющуюся по высоте фазовую добавку к текущей фазе , что и объясняет смысл термина ЛФТ.

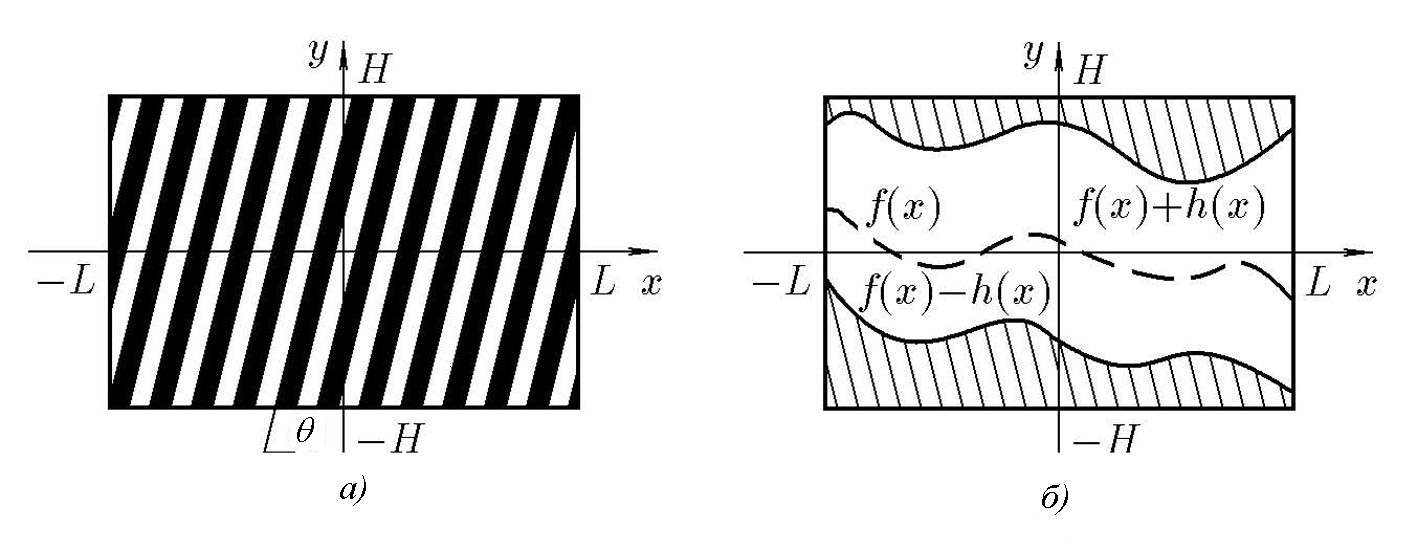
Рис. 1. 13. Составляющие двумерного ОТ: несущий транспарант (а)

и кодирующий транспарант (б)

Двумерный ОТ образуется наложением на ЛФТ кодирующего транспаранта (КТ), который представляет собой двумерную область прозрачности в непрозрачном экране (рис.1.13,б), ограниченную кривыми, задаваемыми функциями .

Функция передачи КТ:

. (1.20)

Двумерный ОТ, являющийся мультипликативной парой НТ (на основе ЛФТ) и КТ, имеет функцию передачи

. (1.21)

Соответствующая комплексная огибающая есть

. (1.22)

Функция полностью определяет импульсную реакцию АОСФ, в котором используется двумерный ОТ.

Найдем импульсную реакцию АОСФ с двумерным ОТ. Представим, что двумерный ОТ помещен в схему АОСФ (рис.1.10а). Акустооптический модулятор возбуждается коротким радиоимпульсом с несущей частотой так, что его комплексную огибающую можно аппроксимировать -функцией:

, (1.23)

где -постоянный коэффициент, пропорциональности, обеспечивающий правильную размерность соотношения.

Поскольку сферическая линза выполняет двумерное преобразование Фурье, то выражение (1.18) для комплексной огибающей тока ФП следует обобщить очевидным образом, учитывая интегрирование по координате y:

. (1.24)

Подставив в (1.24) выражение (1.23) для и используя формулы (1.20)-(1.22), запишем комплексную огибающую импульсной реакции АОСФ в виде

.

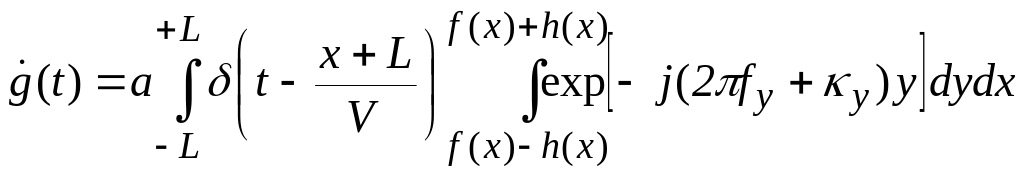Проведя простое интегрирование по , на основании фильтрующих свойств -функции получаем для точки расположения ФП окончательное выражение для комплексной огибающей импульсной реакции:

, , (1.25)

где -апертура АОМ вдоль оси , а смысл функций и понятен из рис.1.13б.

Как видно из этого выражения, с помощью двумерного ОТ можно сформировать импульсную реакцию произвольного вида. При этом закон изменения средней линии области прозрачности КТ обеспечивает нужный закон фазовой модуляции, а закон, по которому изменяется высота области прозрачности, задает закон амплитудной модуляции и также закон фазовой манипуляции (если таковая имеется). Двумерный ОТ на основе ЛФТ устраняет технологические трудности изготовления дифракционной решетки с заданной высокочастотной структурой. Более того, применение в качестве НТ динамической фазовой решетки, роль которой выполняет надлежащим образом ориентированный АОМ, возбуждаемый гармоническим колебанием, вообще снимает проблему изготовления НТ. Реализация же КТ с бинарной, не содержащей высокочастотной структуры функцией прозрачности, при современном уровне развития фотолитографии трудностей не вызывает. Двумерный ОТ нового типа открывает широкие возможности для оперативной, в том числе и электронной, перестройки импульсной реакции АОСФ, для чего достаточно изменить форму и расположение области прозрачности КТ. Это может быть достигнуто при использовании в качестве КТ жидкокристаллической матрицы с управляемой внешним напряжением функцией прозрачности.

Итак, в АОСФ с двумерным ОТ в виде надлежащим образом выбранной мультипликативной пары несущего и кодирующего транспарантов можно производить согласованную фильтрацию радиосигналов длительностью не более с произвольной формой комплексной огибающей. Следует отметить, что двумерный ОТ в алгоритмическом плане эквивалентен одномерному транспаранту, функция пропускания которого имеет комплексную огибающую вида (1.25), т.е.

, .

Из (1.25) следует, что запись, к примеру, бинарных фазоманипулированных сигналов можно осуществлять как путем скачкообразного изменения вдоль оси текущей полувысоты области прозрачности КТ при условии , так и посредством скачкообразного изменения при условии . Легко видеть, что во втором варианте более экономично используется световой поток, дифрагировавший на ОТ. На рис.1.14 показана для примера структура КТ для обработки сигнала, манипулированного по фазе согласно 31-элементной псевдослучайной последовательности. Кодирующий транспарант выполнен по второму варианту, причем принято , а координата средней линии менялась скачкообразно так, чтобы выполнялось соотношение .

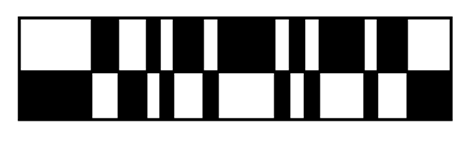
Рис. 1.14. Структура КТ для обработки сигнала, манипулированного по фазе

Очевидно, при записи частотно-модулированных сигналов в структуре кодирующей маски необходимо отражать соответствующие им фазовые функции . На рис.3.16 представлен вид кодирующей маски с записью радиосигнала с линейной частотной модуляцией (ЛЧМ), для которого закон фазовой модуляции является квадратичным. В этом случае ; .

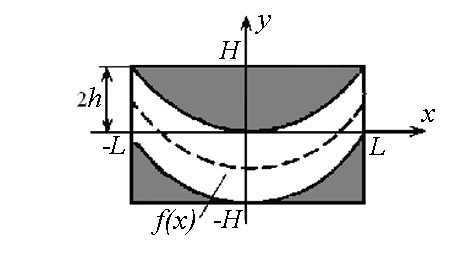
Рис. 1.15. Структура КТ для обработки ЛЧМ-сигнала