2.3. Акустооптический процессор обработки сигналов

антенных решеток

Многофункциональные антенные решетки (АР) являются современными радиоэлектронными комплексами, предназначенными для определения координат и частоты источника электромагнитного излучения в широком интервале углов и большой полосе частот. Решение этой задачи в чисто электронном базисе сталкивается со значительными техническими трудностями. Из антенной техники известно, что распределение комплексной амплитуды электромагнитного поля в апертуре антенны и ее диаграмма направленности связаны пространственным преобразованием Фурье. Этот факт наводит на мысль о возможности применения оптических методов для обработки сигналов ФАР, поскольку в оптических системах пространственное преобразование Фурье осуществляется предельно просто. Первая попытка решения задачи обработки сигналов АР с помощью оптических методов была предпринята Ламбертом в 1965 г.

АОП Ламберта для обработки сигналов, принятых линейной АР, представляет собой, по сути дела, АОСПИ на основе многоканального АОМ (рис.4.6). Сигналы, принятые (2 элементной АР, после гетеродинирования, фильтрации и усиления поступают на входы )-канального АОМ, помещенного в оптическую систему АОСПИ, в котором выполняется двумерное пространственное преобразование Фурье.

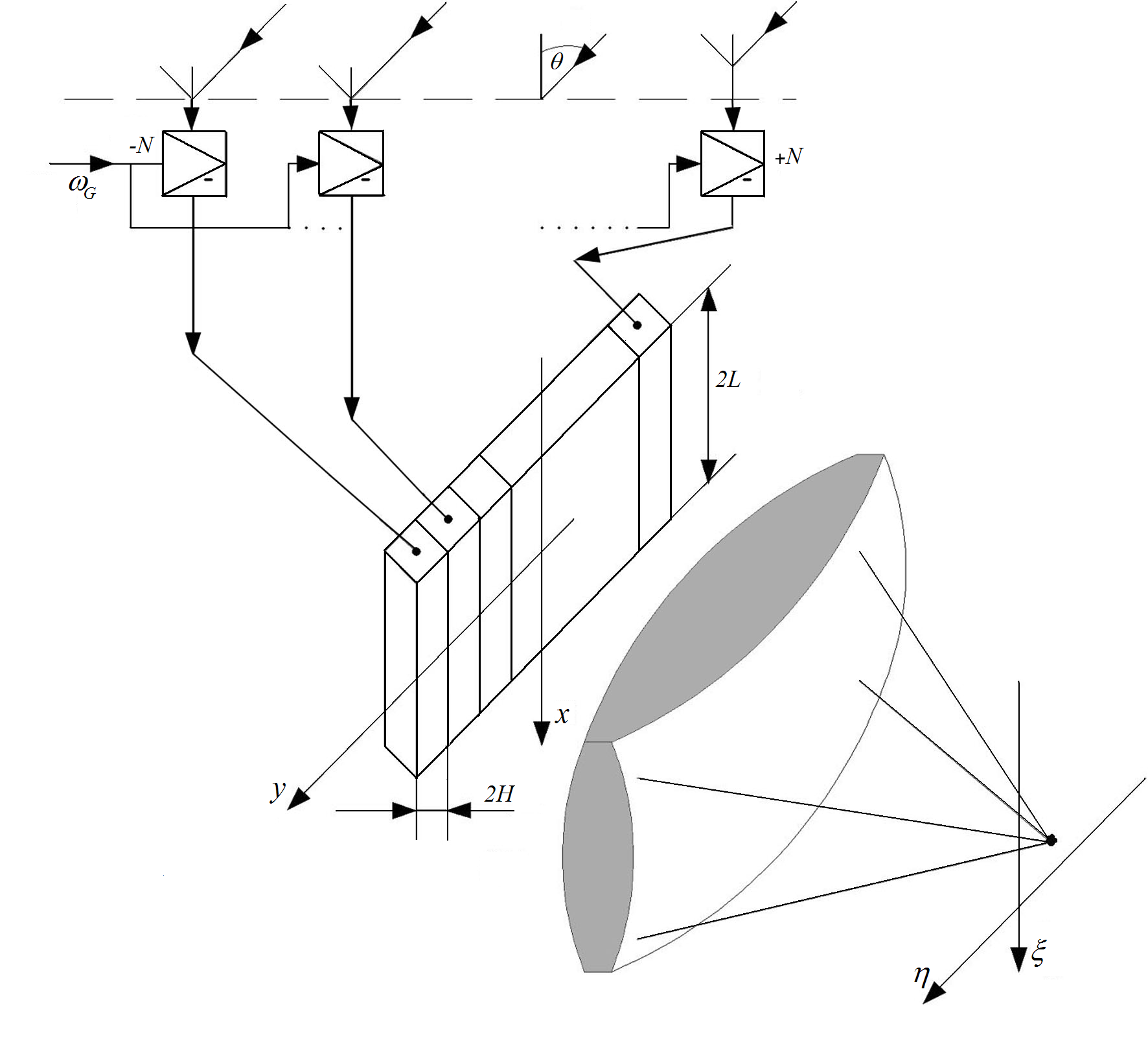Рис.2.6. Акустооптический процессор для обработки сигналов линейной АР

Для определения характеристик АОП найдем распределение интенсивности в плоскости регистрации светового распределения. Сигнал, принятый -м элементом АР и поступающий после гетеродинирования на -й канал многоканального АОМ, имеет вид

. (2.11)

Здесь и законы амплитудной и фазовой модуляции в принятом сигнале, относительная временная задержка сигнала в соседних элементах АР, связанная с направлением на источник соотношением

, (212)

расстояние между элементами АР, скорость света; угловая частота принятого сигнала с учетом возможного доплеровского сдвига частоты, частота общего гетеродина, время прихода сигнала на центральный элемент АР. В линейном режиме дифракции световое поле, дифрагирующее (для определенности) в +1 порядок на сумме сигналов вида (2.11), в выходной плоскости АОМ будет иметь вид

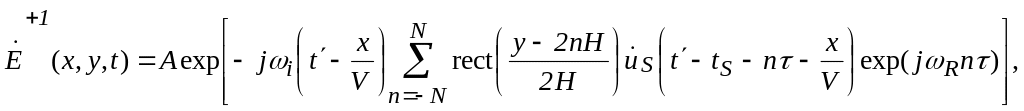
где промежуточная частота, близкая к центральной частоте АОМ;

комплексная огибающая сигнала : ;  смещенное время, коэффициент, в который включены несущественные сомножители. Функция под знаком суммы учитывает многоканальность АОМ, ширина акустического пучка по оси . В результате двумерного преобразования Фурье, осуществляемого сферической линзой Л, в ее фокальной плоскости получается распределение комплексной амплитуды светового поля:

. (2.13)

Выполнив интегрирование по переменной и воспользовавшись формулой суммирования геометрической прогрессии

,

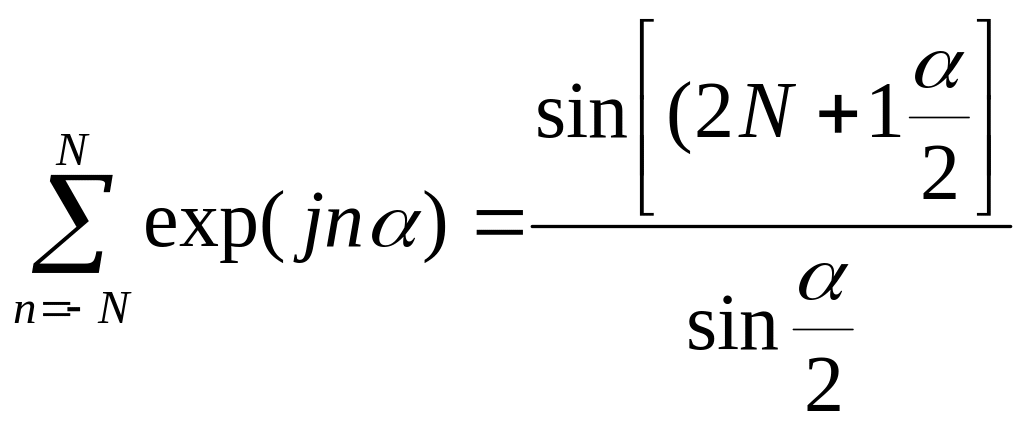образуем выражение для интенсивности дифрагировавшего света

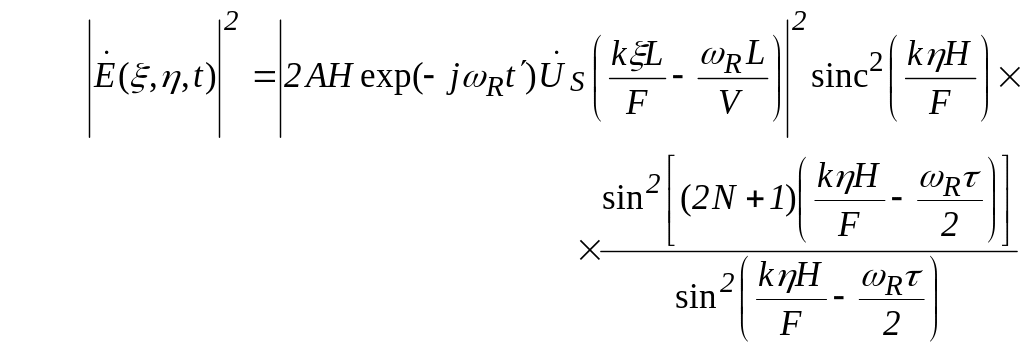. (2.14)

В (2.14) спектр комплексной огибающей сигнала , причем в порядке приближения считается, как это принято в теории АР, , т.е. что комплексная огибающая сигнала не зависит от временной задержки в соответствующем элементе АР. Видно, что двумерное распределение интенсивности света содержит три сомножителя. Первый из нихэто амплитудный спектр принятого сигнала, центрированный вокруг пространственной координаты

, (2.15)

Соотношение (2.15) характерно для АОСПИ и позволяет определить значение несущей частоты принятого сигнала с разрешением по частоте, определяемым временной апертурой АОМ вдоль сигнальной координаты . Второй сомножительфункция отражает факт масштабирования апертуры линейной АР протяженностью в апертуру АОМ вдоль координатной оси с учетом перехода с длины волны , соответствующей радиодиапазону, на оптическую длину волны . Максимум этой функции расположен при , а главный ее максимум имеет ширину но нулям

. (2.16)

Третий сомножитель вида описывает спектр периодической решетки конечной протяженности, иначе говорядиаграмму направленности линейной эквидистантной решетки из элементов. Главный максимум этой функции расположен в точке

. (2.17)

Используя формулу (2.12) и переходя к длинам волн принятого сигнала и света , приведем (2.17) к виду

. (2.18)

Таким образом, положение главного максимума по оси определяет направление на источник излучения (пеленг). Ширина этого максимума по нулям, как легко видеть, есть

, (2.19)

она определяет разрешающую способность процессора по углу прихода сигнала. Действительно, пусть АР принимает два сигнала на одной и той же длине волны с двух различных направлений и (пусть > ). Согласно (2.18) и (2.19) отклики будут разрешимы, если соответствующие максимумы пространственно разнесены по оси не менее чем на . Это значит, что должно быть выполнено условие

,

которое легко приводится к виду

. (2.20)

Это соотношение, в котором , а среднее направление прихода сигналов, является основным в теории линейных АР. Следовательно, АОП обеспечивает разрешение по углу прихода сигнала характерное для АР с заданной апертурой.

Сравнивая (2.16) и (2.19), видим, что в пределах главного лепестка функции размещается лепестков функции . При этом пределы перемещения главного максимума диаграммы направленности согласно (2.18) для углов , изменяющихся от –90⁰ до +90⁰ (обзор полупространства), ограничены областью

. (2.21)

Неравенства (2.21) определяют, таким образом, рабочую область по оси . На границах этой области масштабирующая функция принимает минимальное значение

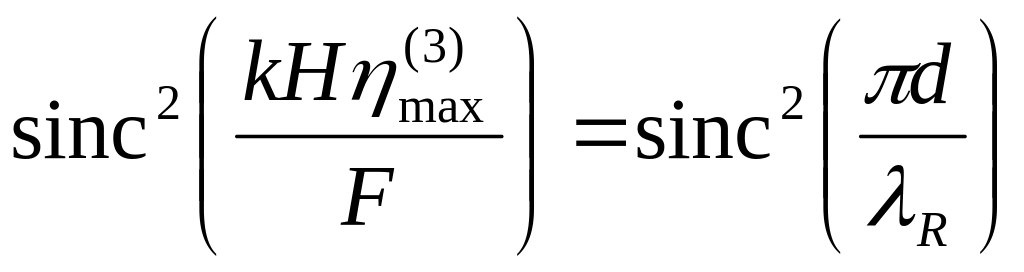. (2.22)

Из антенной техники известно, что для однозначного определения пеленга необходимо, чтобы в зоне видимости имелся бы единственный главный максимум диаграммы направленности. Для этого расстояние между элементами антенной решетки выбирается согласно условию . Считая, что это условие выполнено, получаем оценку

,

которая определяет неравномерность амплитудно-частотной характеристики АОП. В пределах упомянутой рабочей зоны умещается, как нетрудно видеть, количество главных лепестков диаграммы направленности, равное отношению

,

что соответствует количеству разрешаемых (по нулевому критерию) угловых дискретных положений глобального максимума диаграммы направленности линейной элементной АР. Рис.2.7 иллюстрирует приведенные теоретические оценки.

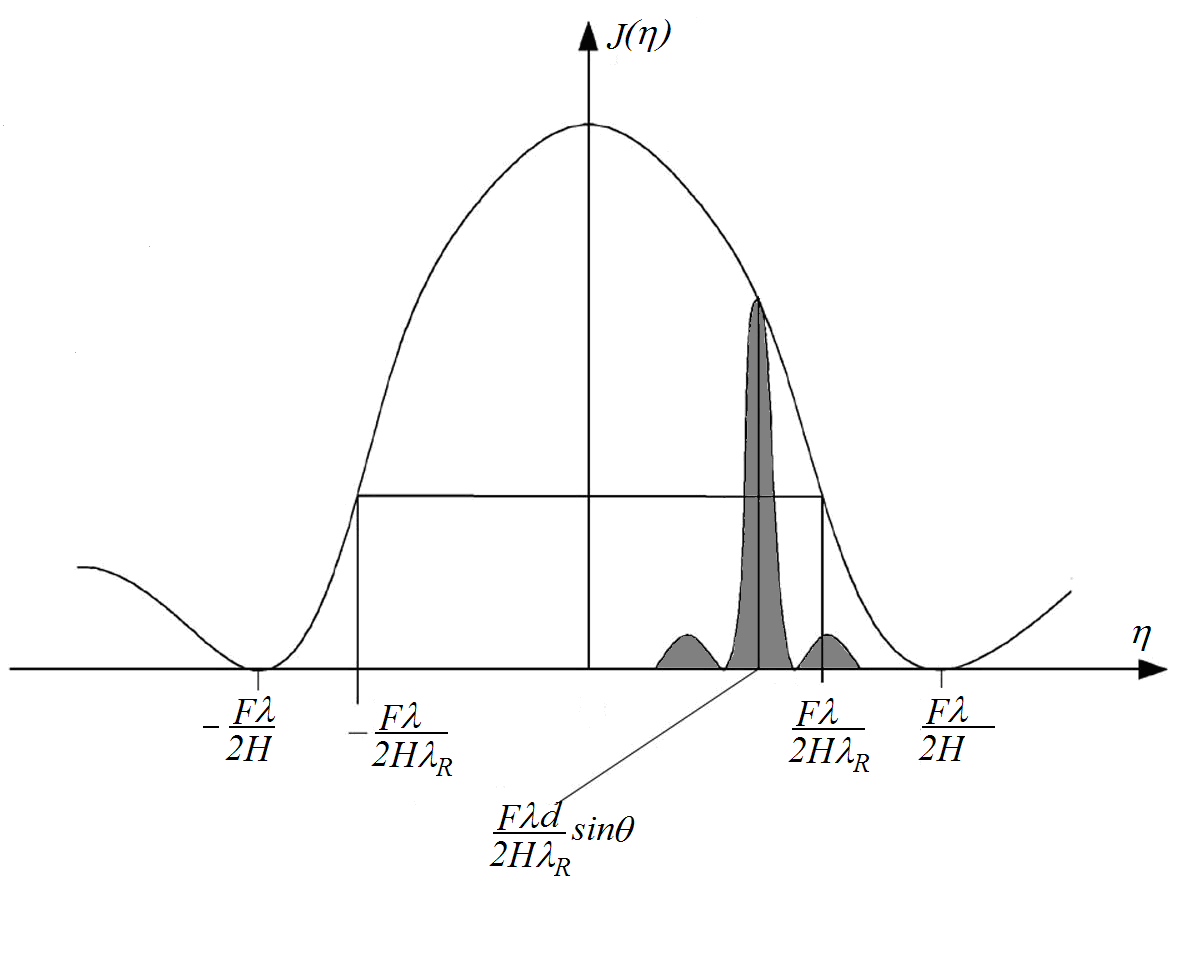
Рис.4.7. Распределение интенсивности света по угловой координате

в выходной плоскости АОП обработки сигналов линейной АР

В обсуждавшемся АОП Ламберта принятые линейной АР сигналы разделяются в оптической системе пространственным образом с помощью многоканального АОМ, т. е. естественным путем. Важным достоинством процессора Ламберта является то, что он позволяет одновременно определять угловые координаты и частоты всех имеющихся в секторе обзора источников. При этом угловое разрешение задается размерами апертуры АР, а частотное разрешениевременной апертурой одиночного канала АОМ. Последнее обстоятельство с учетом того, что временные апертуры реальных АОМ не превосходят нескольких десятков микросекунд, накладывает ограничение на точность определения частоты источника и делает в некоторых случаях невозможным определение доплеровского сдвига частоты. Как отмечалось выше, этот недостаток, присущий всем АОП с пространственным интегрированием, может быть устранен при переходе к процессорам с временным интегрированием.