2.2. Акустооптические анализаторы спектра с временным интегрированием

В спектроанализаторах этого типа в отличие от АОС с пространственным интегрированием частотное разрешение определяется временем накопления заряда на фотоприемнике, что позволяет существенно его повысить. В акустооптических спектроанализаторах с временным интегрированием (АОСВИ) спектр формируется согласно канонической формуле

. (2.6)

Заметим, что ядро этого интегрального преобразования может быть построено на основе ядра , представляющего комплексную огибающую ЛЧМ-сигнала, следующим образом:

Очевидно, для получения спектра по формуле (2.6) с использованием ядра требуется корреляционная процедура, которая может быть реализована в схеме радиочастотного коррелятора со встречными акустическими пучками (рис.1.20). В качестве входных следует при этом использовать следующие сигналы:

,

,

т.е. ЛЧМ-сигнал с прямоугольной огибающей и ЛЧМ-колебание, модулированное по амплитуде анализируемым сигналом . Соответствующие комплексные огибающие имеют вид:

, (2.7)

. (2.8)

Подставляя выражения (2.7) и (2.8) в формулу (1.27), запишем сигнальную составляющую накопленного в ФП заряда

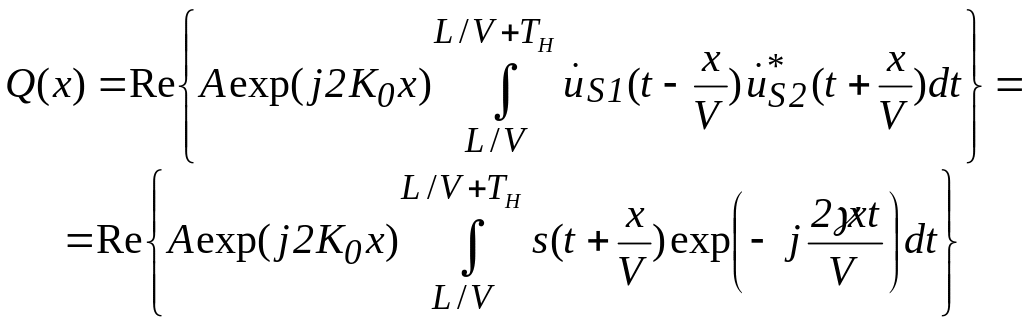, (2.9)

где . Поскольку время накопления , то (2.9) представляет спектр сигнала длительностью , причем считается, что длительность ЛЧМ-сигнала . Также как ВКФ в АОКВИ спектр сигнала модулирует пространственную несущую, представленную в выражении (2.9) множителем . Это влечет за собой те же проблемы с использованием элементов ФП, которые обсуждались применительно к АОКВИ. Основные характеристики АОСВИ корреляционного типа можно определить, взяв в качестве сигнала гармоническое колебание с частотой . Тогда из (4.9) найдем сигнальную составляющую накопленного заряда

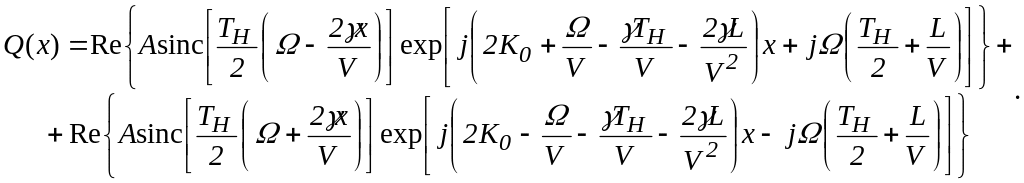(2.10)

Из (4.10) следует, что аппаратная функция АОСВИ представляет собой сумму функций , причем положение главных максимумов определяется формулой , а ширина главного максимума по нулям есть , чему соответствует частотное разрешение . Полоса анализа определяется из очевидного соотношения и оказывается равной девиации частоты отрезка ЛЧМ-сигнала, равного по длительности временной апертуре АОМ. В то же время рабочая полоса АОМ должна быть равна полной девиации ЛЧМ-сигнала . Разрешающая сила АОСВИ рассматриваемого типа есть, очевидно, и совпадает с разрешающей силой АОСПИ. Определив основные рабочие характеристики АОСВИ, дадим физическую интерпретацию его работы. Пусть на оба входа коррелятора на встречных акустических пучках (рис.1.20) поступает одно и то же ЛЧМ колебание с прямоугольной огибающей. В плоскости ФП, которая является плоскостью изображения обеих апертур АОМ, интерферируют две световые волны, распространяющиеся под углами к оптической оси. Интерференционная картина имеет пространственный период , а интенсивность света в каждой точке изменяется с частотой биений , которая определяется разностью частот интерферирующих световых волн и изменяется в пространстве линейно. На рис.2.5 показаны законы изменения частоты света обеих волн вдоль апертуры ФП.

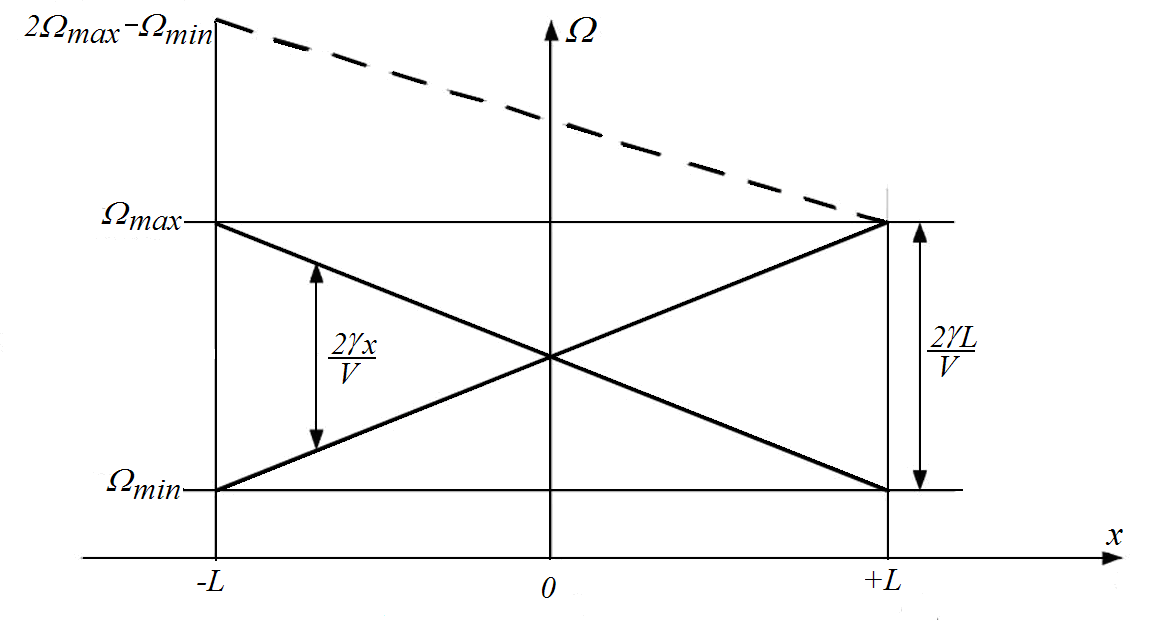
Рис.2.5. Изменение частотного сдвига дифрагировавших световых волн

вдоль апертуры фотоприемника.

В центре частота биений нулевая, а по краяммаксимальная, равная полосе анализа . Таким образом с помощью двух ЛЧМ колебаний создается световая сетка частот, равномерно распределенная по апертуре ФП. Когда на одно из ЛЧМ колебаний посредством амплитудной модуляции накладывается анализируемый сигнал, то описанное световое распределение умножается на этот сигнал. ФП преобразует это световое распределение в заряд, накопленный за время , что математически описывается формулой (2.9).

Три замечания в заключение. Во-первых, из рис.2.5 видно, что апертуры АОМ при такой организации анализа используются лишь на половину, что вдвое сокращает полосу анализа. Этот недостаток можно устранить, если сместить начальную частоту одного из колебаний на величину (штриховая линия на рис.2.5). При этом частота биений будет распределена по апертуре ФП от нулевой на правом краю до на левом. Во-вторых, поскольку спектр сигнала формируется на пространственной световой несущей, для устранения проблем с количеством необходимых элементов ФП для его воспроизведения возможно использовать структуру аналогичную двумерному АОКВИ. В-третьих, в анализируемом АОСВИ не полностью используется рабочая полоса частот АОМ, поскольку полоса анализа составляет лишь . Увеличить полосу анализа и довести ее до величины полосы АОМ позволяют двумерные АОС с пространственным и временным интегрированием.