Функциональная электроника

Конспект лекций

Раздел 1 акустооптические процессоры Глава 1. Акустооптические процессоры корреляционного типа

1.1. Акустооптический модулятор

Разновидностью когерентных оптических процессоров, ориентированных на обработку радиосигналов, являются акустооптические процессоры (АОП), в которых для ввода радиосигналов в оптическую систему используются акустооптические модуляторы (АОМ), работающие на эффекте акустооптического взаимодействия. Можно сказать, что АОМ выполняют функции динамического сигнального транспаранта. Акустооптическое взаимодействие внешне проявляется как дифракция света на акустических волнах в прозрачной среде. АОМ представляет собой (рис.3.1) прозрачный плоскопараллельный звукопровод 1, выполненный из стекол или монокристаллов, к металлизированному торцу 2 которого термокомпрессией крепится пластинка 3 из пьезоэлектрика; к ее обкладкам прикладывается переменное напряжение.

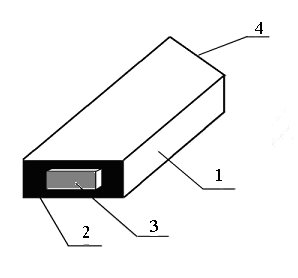
Рис.1.1. Акустооптический модулятор

Под действием этого напряжения возникают механические колебания пластинки пьезоэлектрика, возбуждающие в звукопроводе бегущую акустическую волну, которая поглощается на дальнем (скошенном) торце. Распространяющаяся в упругой среде бегущая акустическая волна создает пространственно-временное распределение давления. Изменению давления во времени и пространстве соответствует пространственно-временное изменение плотности и, следовательно, коэффициента преломления среды. Падающая на такую среду световая волна рассеивается на вариациях коэффициента преломления, в результате чего образуется дифракционное световое поле. Характеристики этого поля зависят от частоты акустической волны и взаимной ориентации обоих полей в пространстве, т.е. от геометрии их взаимодействия. Существуют два основных режима дифракции света на акустических волнах, которые теоретически трактуются с различных физических позиций.

1.1.1. Режимы дифракции Рамана-Ната и Брэгга

В режиме дифракции Рамана-Ната дифрагированное световое поле рассматривается как результат прохождения света через тонкую чисто фазовую пластинку с переменным во времени и пространстве коэффициентом преломления. Дифракция световых волн на статической синусоидальной фазовой решетке рассматривалась в разделе 1.2.5. Полученные там результаты с некоторыми изменениями, отражающими динамический характер акустической волны, переносятся на режим дифракции Рамана-Ната. Пусть в плоскопараллельной пластинке толщиной , длиной (рис.3.2) распространяется гармоническая акустическая волна с частотой со скоростью вдоль оси . Эта волна создает изменение коэффициента преломления среды по

закону бегущей волны

,

где -волновое число акустической волны, -длина акустической волны, -невозмущенное значение коэффициента преломления материала пластинки, а -амплитуда его изменения.

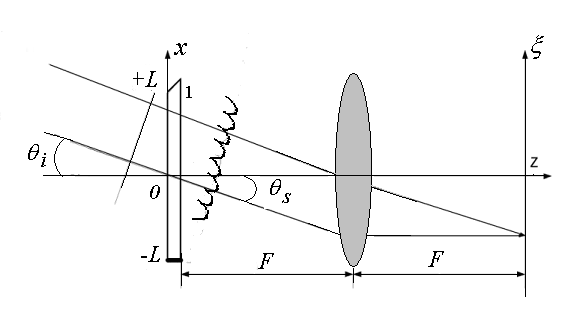
Рис. 1. 2. Геометрия акустооптического взаимодействия

в режиме дифракции Рамана-Ната

Падающая под углом к оси горизонтально поляризованная плоская световая волна на ²входе² АОМ (при ) имеет вид

,

где волновое число света в вакууме, и длина волны и круговая частота света. Здесь и в дальнейшем зависимость от времени монохроматического оптического поля принята в виде .

В выходной плоскости пластинки ( ) с учетом приобретаемой световой волной фазовой задержки получим

, (1.1)

где введен индекс фазовой модуляции света .

Дифрагировавшее световое поле, наблюдаемое в фокальной плоскости цилиндрической линзы, есть

После использования представления стоящей под интегралом экспоненты в виде известного ряда с коэффициентами в виде функций Бесселя после интегрирования получим

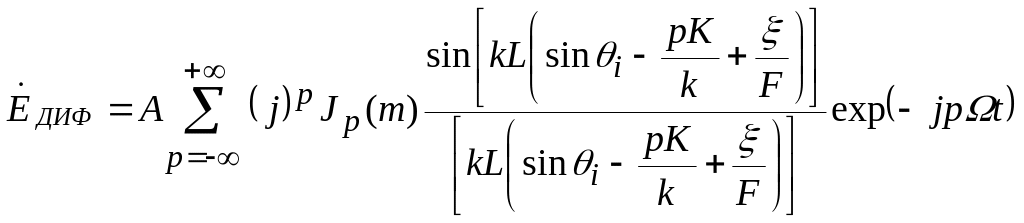, (1.2)

где координата в задней фокальной плоскости линзы (плоскости пространственных частот), - постоянный множитель. Из (1.2) видно, что дифрагированное поле представляет собой совокупность максимумов с координатами, определяемыми из соотношения

По геометрическим соображениям (рис.1.2) , и можно определить направления на дифракционные порядки

(1.3)

При записи (1.3) считалось, как это обычно имеет место на практике, что углы падения и дифракции световой волны малы . Максимальное значение интенсивности света в дифракционном порядке с номером пропорционально квадрату функции Бесселя: , а распределение интенсивности в окрестности максимума задается функцией вида . При обычно встречающихся на практике амплитудах акустических волн индекс фазовой модуляции , поэтому число дифракционных максимумов невелико. Из (1.2) видно, что частота света в -ом дифракционном порядке , т.е. сдвинута вверх или вниз относительно частоты падающего света на величину, кратную частоте падающего света, что является проявлением эффекта Доплера рассеяния света на движущихся неоднородностях коэффициента преломления. Выражение (1.2) позволяет проанализировать также угловую и частотную зависимости акустооптического взаимодействия в режиме дифракции Рамана-Ната. Очевидно, зависимость дифракционной картины от угла падения состоит единственно в ее перемещении как неизменного целого в пространстве (рис.1.3). Аналогично, изменение частоты акустической волны влечет за собой только изменение угловых расстояний между дифракционными порядками и соответствующих частотных сдвигов света в этих порядках, в остальном же структура дифракционной картины сохраняется.

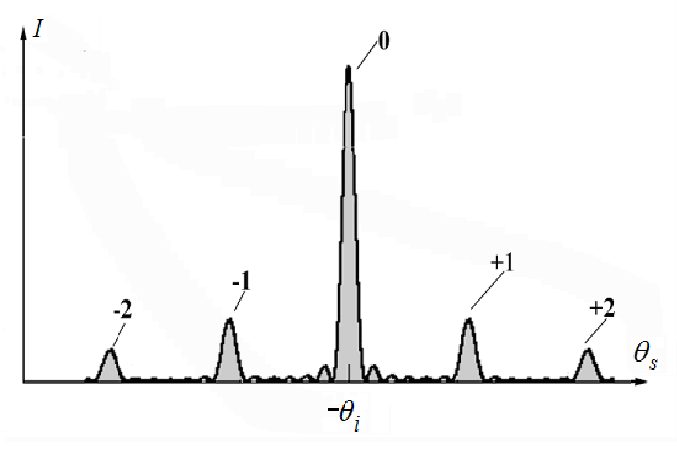
Рис. 1.3. Дифракционная картина в режиме Рамана-Ната

Таким образом, для дифракции света на акустических волнах в режиме Рамана-Ната характерны: симметрия дифракционной картины относительно нулевого дифракционного порядка и отсутствие угловой и частотной избирательности.

В акустооптике установлено, что режим дифракции Рамана-Ната реализуется при условии

<<1, (1.4)

где − так называемый параметр дифракции. Из (1.4) видно, что этот режим осуществляется при достаточно тонких акустических пучках ( мало) и низких частотах ( велико).

Режим дифракции Брэгга, напротив, реализуется при условии >>1, что достигается для широких акустических пучков на высоких частотах. В этом случае на формирование дифрагировавшего светового поля существенное влияние оказывает объемный характер акустооптического взаимодействия. В физическом отношении данный режим дифракции аналогичен рассеянию рентгеновских лучей на межатомных плоскостях кристаллической решетки твердого вещества. Роль таких плоскостей играют гребни акустической волны - области, где (на рис.1.4 эти плоскости условно изображены горизонтальными пунктирными линиями).

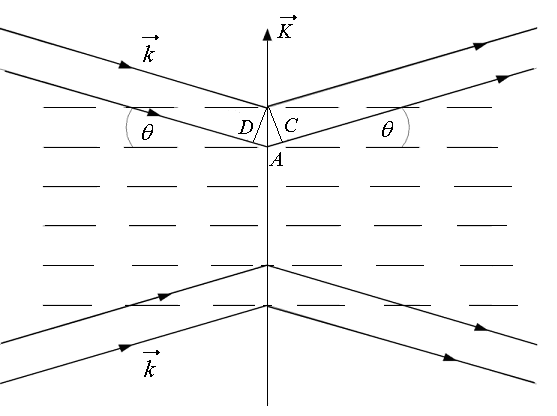
Рис. 1.4. Интерпретация акустооптического взаимодействия

в режиме дифракции Брэгга

Отраженные различными плоскостями лучи приходят в фазе и формируют дифрак ционный максимум при условии, что их разность хода кратна λ, т. е. ( -целое число). Из рис.1.4 видно, что . Поэтому условие формирования дифракционного максимума имеет вид

(1.5)

Угол падения , при котором происходит интенсивная дифракция, называется углом Брэгга. В режиме дифракции Брэгга, кроме невозмущенного поля, образуется только один дифракционный (+1 или –1) порядок, что зависит от знака угла падения светового пучка на волновой фронт акустической волны (рис.1.4). Соотношение (1.5) указывает на избирательный характер акустооптического взаимодействия в режиме дифракции Брэгга, как по частоте, так и по углу падения световой волны. Помимо этого, картина дифракции асимметрична относительно направления падения световой волны (рис.1.5). Этим режим дифракции Брэгга отличается от режима Рамана-Ната.

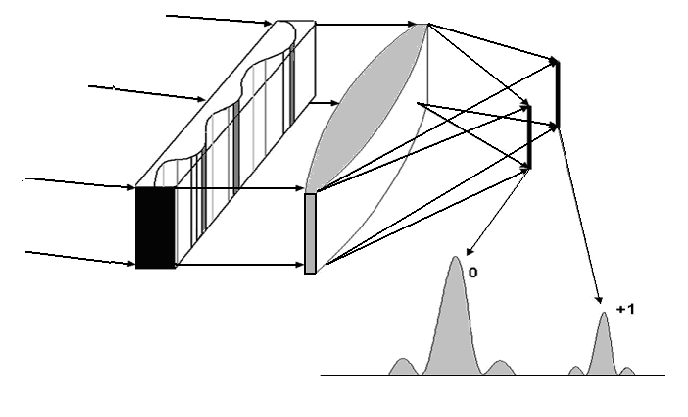
Рис. 1.5. Акустооптический модулятор в режиме дифракции Брэгга

В технике АОП для ввода радиосигналов в оптическую систему используются АОМ, работающие в обоих режимах дифракции. При этом в случае дифракции Рамана-Ната в большинстве случаев реализуется линейный режим, когда индекс фазовой модуляции <<1, при этом, кроме нулевого порядка, имеются только 1 дифракционные порядки. Эффективность модуляции световой волны акустическим сигналом оценивается отношением (см. раздел 1.2.7.)

,

где -интенсивность света в одном из первых дифракционных порядков, а -интенсивность падающего света. Для режима дифракции Рамана-Ната на основании (1.2) находим

.

В случае дифракции Брэгга известно, что

. (1.6)

Соответствующие кривые, называемые модуляционными характеристиками, приведены на рис.1.6.

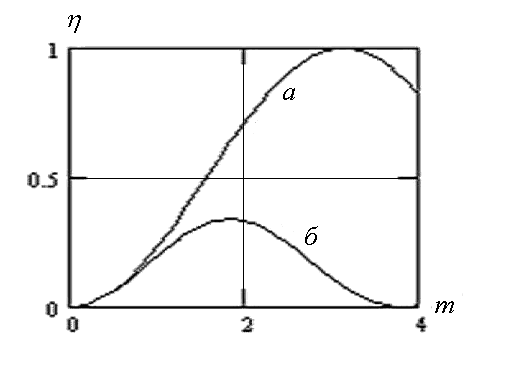
Рис. 1.6. Модуляционные характеристики АОМ

в режиме дифракции Брэгга (а) и Рамана-Ната (б)

Видно, что работа АОМ в режиме дифракции Брэгга является значительно более эффективной.