
Механика
Задание 1 (выберите один вариант ответа).
Два
тела брошены под одним и тем же углом к
горизонту с начальными скоростями ![]() и
и ![]() .
Если сопротивлением воздуха пренебречь,
то соотношение дальностей
полета
.
Если сопротивлением воздуха пренебречь,
то соотношение дальностей
полета ![]() равно...
Варианты
ответов: 1)
равно...
Варианты
ответов: 1) ![]() ; 2)4; 3)
2; 4)
; 2)4; 3)
2; 4) ![]() .
.
 Решение: Дальность
полета тела, брошенного под углом к
горизонту, определяется по закону
равномерного движения:
Решение: Дальность
полета тела, брошенного под углом к
горизонту, определяется по закону
равномерного движения:
|
(1) |
![]()
|
(2) |
Время
полета равно удвоенному времени поднятия
тела на максимальную высоту (точка А),
где вертикальная скорость становится
равной 0. Запишем в скалярном виде закон
скорости движения тела в вертикальном
направлении и выразим время движения
до точки A: ![]() ,
в т.
,
в т.![]()
![]() ,
отсюда
,
отсюда
![]()
Полное
время движения тел (до т.![]() ):
):
|
(3) |
|
(4) |
Подставим
значение ![]() и
и ![]() в
(1.1)
и (1.2)
соответственно и найдем дальность
полета для каждого тела.
в
(1.1)
и (1.2)
соответственно и найдем дальность
полета для каждого тела.
![]()
Определим искомое отношение:
![]()
Ответ: 4.
Задание 2.
Материальная
точка движется по окружности с постоянным
тангенциальным ускорением. Если проекция
тангенциального ускорения на направление
скорости положительна, то величина
нормального ускорения:
1) уменьшается; 2)
увеличивается; 3) не
изменяется
Решение: по
условию задачи ![]() ,
известно, что
,
известно, что ![]() следовательно,
скорость точки изменяется со временем
по линейному закону:
следовательно,
скорость точки изменяется со временем
по линейному закону: ![]() 1.
Поскольку нормальное ускорение связано
с линейной скоростью соотношением:
1.
Поскольку нормальное ускорение связано
с линейной скоростью соотношением:
![]() и
и ![]() растет,
то значение нормального ускорения будет
увеличиваться.
Ответ: увеличивается.
растет,
то значение нормального ускорения будет
увеличиваться.
Ответ: увеличивается.
Задание 3.
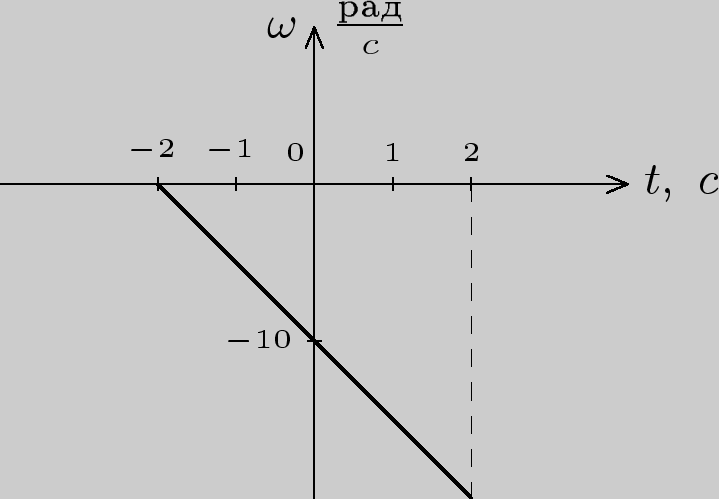
Тело
вращается вокруг неподвижной оси.
Зависимость угловой скорости от
времени ![]() изображена
на рисунке. Тангенциальное ускорение
точки, находящейся на расстоянии 1 метр
от оси вращения, равно:
1)
изображена
на рисунке. Тангенциальное ускорение
точки, находящейся на расстоянии 1 метр
от оси вращения, равно:
1) ![]() ; 2)
; 2) ![]() ;
3)
;
3) ![]() ; 4)
; 4) ![]() .
Решение: В
общем виде зависимость
имеет
вид:
.
Решение: В
общем виде зависимость
имеет
вид: ![]() С
учетом конкретных данных, полученных
из графика, запишем:
С
учетом конкретных данных, полученных
из графика, запишем:
![]() Определим
угловое ускорение (коэффициент при
Определим
угловое ускорение (коэффициент при ![]() ):
):
![]()
Учитывая связь между тангенциальным и угловым ускорением,
![]() рассчитаем
искомое тангенциальное
ускорение:
рассчитаем
искомое тангенциальное
ускорение:
![]()
![]() Задание
4.
Материальная
точка двигалась вдоль оси
Задание
4.
Материальная
точка двигалась вдоль оси ![]() равномерно
с некоторой скоростью
равномерно
с некоторой скоростью ![]() .
Начиная с момента времени
.
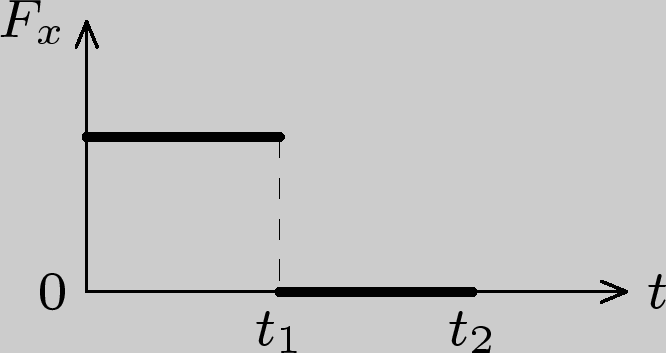
Начиная с момента времени ![]() на
нее стала действовать сила
на
нее стала действовать сила ![]() ,
график зависимости от времени которой
представлен на рисунке:
,
график зависимости от времени которой
представлен на рисунке:
 Графиком,
правильно отражающим зависимость
величины проекции импульса материальной
точки, будет:
1)
Графиком,
правильно отражающим зависимость
величины проекции импульса материальной
точки, будет:
1)
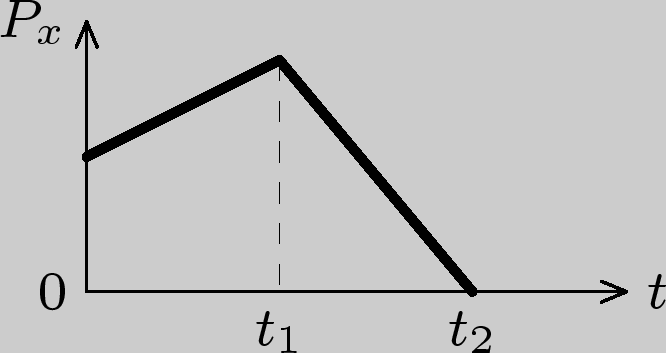 2)
2)
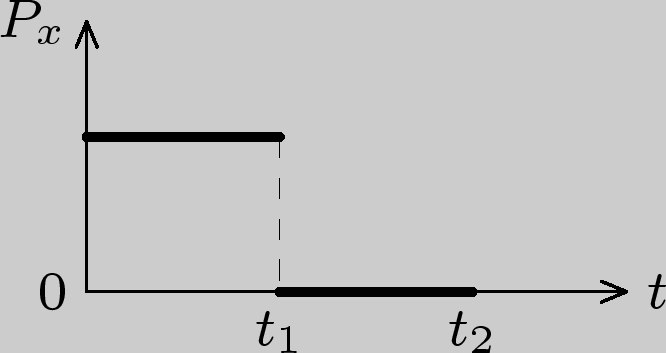
3)
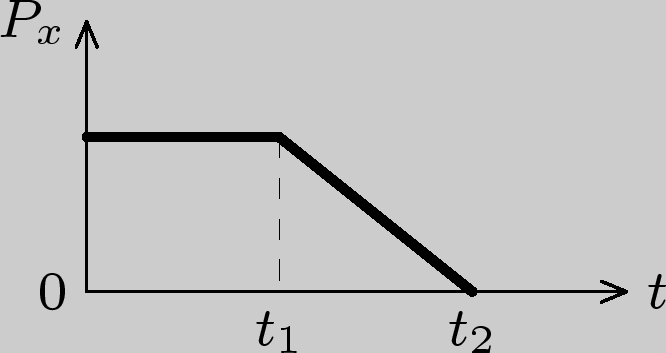
4)
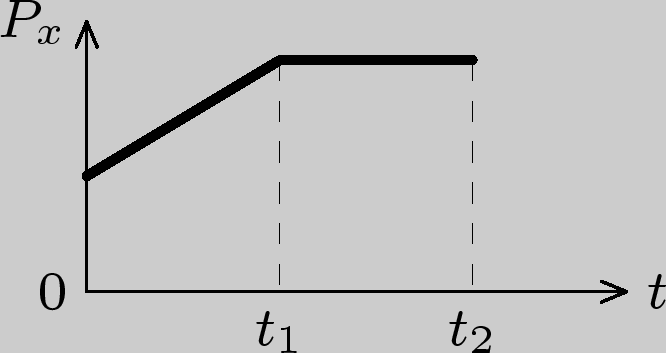 Решение: На
участке
Решение: На
участке ![]() на
тело действует постоянная сила,
следовательно, тело движется с постоянным
ускорением. При этом скорость меняется
по закону:
на
тело действует постоянная сила,
следовательно, тело движется с постоянным
ускорением. При этом скорость меняется
по закону: ![]() ,
то есть линейно растет со временем.
Проекция импульса материальной
точки:
,
то есть линейно растет со временем.
Проекция импульса материальной
точки: ![]() также
линейно растет со временем на участке
.
(Это первый или четвертый вариант
графика.) Рассмотрим участок, соответствующий
времени
также
линейно растет со временем на участке
.
(Это первый или четвертый вариант
графика.) Рассмотрим участок, соответствующий
времени ![]() .
Сила на этом участке не действует на
материальную точку и равна
.
Сила на этом участке не действует на
материальную точку и равна ![]() .
Следовательно, точка движется без
ускорения с постоянной скоростью, и
импульс не меняется со временем. Графиком,
правильно отражающим зависимость
величины проекции импульса от времени,
будет график 4.
Ответ: график
4.
.
Следовательно, точка движется без
ускорения с постоянной скоростью, и
импульс не меняется со временем. Графиком,
правильно отражающим зависимость
величины проекции импульса от времени,
будет график 4.
Ответ: график
4.
Задание 5 (выберите один вариант ответа).
Система
состоит из трех шаров с массами ![]() ,
, ![]() ,
, ![]() ,
которые движутся так, как показано на
рисунке.
,
которые движутся так, как показано на
рисунке.
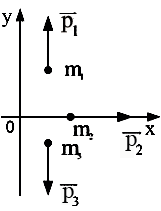
Если
скорости шаров равны ![]() ,
, ![]() ,
, ![]() ,
то величина скорости центра масс этой
системы в м/с равна...
,
то величина скорости центра масс этой
системы в м/с равна...
Варианты
ответов: 1) ![]() ; 2)
4; 3)
; 2)
4; 3) ![]() ; 4)
10.
; 4)
10.
 Решение: Скорость
центра масс замкнутой системы материальных
точек:
Решение: Скорость
центра масс замкнутой системы материальных
точек:
|
(5) |
Для
определения модуля скорости центра
масс найдем проекции выражения (1.5)
на оси ![]() и
и ![]() .
Тогда:
.
Тогда:
![]()
Произведем соответствующие расчеты:
![]()
![]()
![]()
Ответ: ![]()
Задание 6 (выберите один вариант ответа).
Две
материальные точки одинаковой массы
движутся с одинаковой угловой скоростью
по окружностям радиусами ![]() .
При этом отношение моментов импульса
точек
.
При этом отношение моментов импульса
точек ![]() равно...
равно...
Варианты ответов: 1) 2; 2) 4; 3) 1/4; 4) 1/2.
 Решение: Момент
импульса материальной точки:
Решение: Момент
импульса материальной точки: ![]() Скорости
точек соответственно:
Скорости
точек соответственно:
![]()
Запишем выражения для моментов импульса точек в скалярном виде с учетом данных задачи:
|
(6) |
|
(7) |
Найдем искомое отношение, разделив (1.6) на (1.7):
Ответ: 4.
Задание 7.
Если момент инерции тела увеличить в 2 раза и угловую скорость его вращения увеличить в 2 раза, то момент импульса тела...
