
- •Билет № 1
- •Вопрос 1
- •Вопрос 2
- •Билет № 2
- •Вопрос 1
- •Билет №3
- •Вопрос 1
- •Билет №3
- •Вопрос 2
- •Теорема о связи дифференцируемости и непрерывности.
- •Билет № 4
- •Вопрос 1
- •Билет № 4
- •Вопрос 2
- •Билет № 5
- •Вопрос 1
- •Билет № 5
- •Вопрос 2
- •Билет № 6
- •Вопрос 1
- •Предел функции при , геометрическая интерпретация
- •Билет № 6
- •Вопрос 2
- •Билет № 7
- •Вопрос 1
- •Билет №7
- •Вопрос 2
- •Билет №8
- •Вопрос 1
- •Вопрос 2
- •Билет №9
- •Вопрос 1
- •Билет №9
- •Вопрос 2
- •Билет №10
- •Вопрос 1
- •Билет №10
- •Вопрос 2
- •Билет №11
- •Вопрос 1
- •Билет №12
- •Билет №12
- •Билет №13
- •Билет №13
- •Вопрос 2
- •Билет №14
- •Вопрос 1
- •Билет №14
- •Вопрос 2
- •Билет №15
- •Вопрос 1
- •Билет №15
- •Вопрос 2
- •Билет №16
- •Вопрос 1
- •Билет №16
- •Вопрос 2
- •Билет №19
- •Вопрос 1
- •Вопрос 2
- •Билет №20
- •Вопрос 1
- •Билет №20
- •Вопрос 2
- •Билет №21
- •Билет №22
- •Билет №23
- •Вопрос 1
- •Билет №23
- •Вопрос 2
- •Билет №24
- •Вопрос 1
- •Билет №24
- •Вопрос 2
- •Билет №25
- •Вопрос 1
- •Вопрос 2
- •Вопрос 1
- •Вопрос 2
- •Билет №27
- •Вопрос 1
- •Билет №27
- •Вопрос 2
- •Билет №28
- •Вопрос 1
- •Билет №28
- •Вопрос 2
- •Билет №29
- •Вопрос 1
- •Вопрос 2
- •Билет №30
- •Вопрос 1
- •Билет №31
- •Вопрос 1
- •Вопрос 2
- •Билет №32
- •Вопрос 1
- •Билет №32
- •Вопрос 2
Билет № 1
Вопрос 1


Последовательность, имеющая предел, называется сходящийся.
Необходимое условие сходимости: Сходящаяся последовательность ограничена.
Достаточное условие сходимости: Монотонная ограниченная последовательность имеет предел
Примеры:
Последовательность xn = 1/n является сходящейся и имеет предел 0.
Последовательность 1, 0, – 1, 0, 1, 0, – 1, … не имеет предела.
Последовательность xn = n3 не является сходящейся, но имеет предел

Число e — математическая константа, основание натурального логарифма, иррациональное и трансцендентное число (вещественное или комплексное число, не являющееся алгебраическим).
Вопрос 2
Теорема Лагранжа.
Теор.7.3.
Пусть функция f
(х):
1. непрерывна на отрезке [a,b];
2. дифференцируема в каждой точке
интервала (a,b).
Тогда на интервале (a,b)
найдётся точка с
(a<с<b),
в которой
 .
.
Д ок-во.
Рассмотрим на отрезке [a,b]
вспомогательную функцию
ок-во.
Рассмотрим на отрезке [a,b]
вспомогательную функцию
 .
Эта функция удовлетворяет всем условиям
теоремы Ролля (она 1. непрерывна как
разность между непрерывной f
(х)
и непрерывной линейной функцией; 2. в
любой точке интервала (a,b)
имеет производную
.
Эта функция удовлетворяет всем условиям
теоремы Ролля (она 1. непрерывна как
разность между непрерывной f
(х)
и непрерывной линейной функцией; 2. в
любой точке интервала (a,b)
имеет производную
 ;
3. на концах отрезка [a,b]
принимает одинаковые значения:
;
3. на концах отрезка [a,b]
принимает одинаковые значения:

 ).
Следовательно, по теореме Ролля, с(a,b),
для которой
).
Следовательно, по теореме Ролля, с(a,b),
для которой
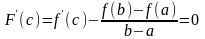 ,
т.е.
.
,
т.е.
.
Геометрический
смысл теоремы Лагранжа
: так как отношение
 равно угловому коэффициенту секущей
АС, на кривой АС найдётся по крайней
мере одна точка
равно угловому коэффициенту секущей
АС, на кривой АС найдётся по крайней
мере одна точка
 ,
в которой касательная параллельна хорде
АС. Следующая из теоремы Лагранжа формула
,
в которой касательная параллельна хорде
АС. Следующая из теоремы Лагранжа формула
 называется формулой
конечных приращений Лагранжа,
она позволяет оценить приращение функции
на отрезке [a,b]
через приращение аргумента и оценку
значений производной на интервале (a,b)
и часто применяется в математическом
анализе.
А) да б) нет
называется формулой
конечных приращений Лагранжа,
она позволяет оценить приращение функции
на отрезке [a,b]
через приращение аргумента и оценку
значений производной на интервале (a,b)
и часто применяется в математическом
анализе.
А) да б) нет
Билет № 2
Вопрос 1




Вопрос
2 Производной
функции
y=f(x)
в точке x0
называется предел отношения приращения
функции к приращению аргумента, когда
приращение аргумента стремится к нулю.

Билет №3
Вопрос 1
Функция
y=f(x) называется бесконечно малой
при x→a или при x→∞, если
![]() или
или
![]() ,
т.е. бесконечно малая функция – это
функция, предел которой в данной точке
равен нулю.
,
т.е. бесконечно малая функция – это
функция, предел которой в данной точке
равен нулю.
Примеры.
Функция f(x)=(x-1)2 является бесконечно малой при x→1, так как

Функция f(x) = tgx – бесконечно малая при x→0.
f(x) = 1/x– бесконечно малая при x→∞.
Теорема. Если функция
y=f(x) представима при x→a в виде
суммы постоянного числа b и бесконечно
малой величины α(x): f (x)=b+ α(x) то
![]() .
.
Обратно, если , то f (x)=b+α(x), где a(x) – бесконечно малая при x→a.
Доказательство.
Докажем первую часть утверждения. Из равенства f(x)=b+α(x) следует |f(x) – b|=| α|. Но так как a(x) – бесконечно малая, то при произвольном ε найдется δ – окрестность точки a, при всех x из которой, значения a(x) удовлетворяют соотношению |α(x)|<ε. Тогда |f(x) – b|< ε. А это и значит, что .
Если , то при любом ε>0 для всех х из некоторой δ – окрестность точки a будет |f(x) – b|< ε. Но если обозначимf(x) – b= α, то |α(x)|<ε, а это значит, что a – бесконечно малая.
Основные свойства бесконечно малых функций.
Теорема 1. Алгебраическая сумма двух, трех и вообще любого конечного числа бесконечно малых есть функция бесконечно малая.
Доказательство.
Приведем доказательство для двух
слагаемых. Пусть f(x)=α(x)+β(x), где
![]() и
и
![]() .
Нам нужно доказать, что при произвольном
как угодно малом ε>0 найдется δ>0,
такое, что для x, удовлетворяющих
неравенству |x – a|<δ, выполняется
|f(x)|< ε.
.
Нам нужно доказать, что при произвольном
как угодно малом ε>0 найдется δ>0,
такое, что для x, удовлетворяющих
неравенству |x – a|<δ, выполняется
|f(x)|< ε.
Итак, зафиксируем произвольное число ε>0. Так как по условию теоремы α(x) – бесконечно малая функция, то найдется такое δ1>0, что при |x – a|<δ1 имеем |α(x)|< ε/2. Аналогично, так как β(x) – бесконечно малая, то найдется такое δ2>0, что при |x – a|<δ2 имеем | β(x)|< ε/2.
Возьмем δ=min{ δ1, δ2}.Тогда в окрестности точки a радиуса δбудет выполняться каждое из неравенств |α(x)|< ε/2 и | β(x)|< ε/2. Следовательно, в этой окрестности будет
|f(x)|=| α(x)+β(x)| ≤ |α(x)| + | β(x)| < ε/2 + ε/2= ε,
т.е. |f(x)|<ε, что и требовалось доказать.
Теорема 2. Произведение бесконечно малой функции a(x) на ограниченную функцию f(x) при x→a (или при x→∞) есть бесконечно малая функция.
Доказательство. Так как функция f(x) ограничена, то существует число М такое, что при всех значениях x из некоторой окрестности точки a|f(x)|≤M. Кроме того, так как a(x) – бесконечно малая функция при x→a, то для произвольного ε>0 найдется окрестность точки a, в которой будет выполняться неравенство |α(x)|< ε/M. Тогда в меньшей из этих окрестностей имеем | αf|< ε/M= ε. А это и значит, что af – бесконечно малая. Для случая x→∞ доказательство проводится аналогично.
Из доказанной теоремы вытекают:
Следствие 1. Если
и
,
то
![]() .
.
Следствие 2. Если
и
c=const, то
![]() .
.
Теорема 3. Отношение бесконечно малой функции α(x) на функцию f(x), предел которой отличен от нуля, есть бесконечно малая функция.
Доказательство. Пусть
![]() .
Тогда 1/f(x) есть ограниченная функция.
Поэтому дробь
.
Тогда 1/f(x) есть ограниченная функция.
Поэтому дробь
![]() есть
произведение бесконечно малой функции
на функцию ограниченную, т.е. функция
бесконечно малая.
есть
произведение бесконечно малой функции
на функцию ограниченную, т.е. функция
бесконечно малая.
