2.1.5. Произвольный сферический излучатель.
Задача формулируется следующим образом:
,
-
оператор углов.
-
произвольная функция углов.
Задача решается методом разделения переменных:
,
.
Для угловой функции получаем уравнения:
,
,
или для переменной :
,
,
-
присоединённые полиномы Лежандра,
образующие полную ортогональную систему
функций:
,
,
-
общее решение задачи.
Для
нахождения произвольных постоянных
общего решения
нужно представить граничную функцию в
виде аналогичного разложения по
собственным функциям граничной задачи:
которые
образуют полную ортогональную систему
функций на поверхности сферы
единичного радиуса.
Соотношение
ортогональности имеет вид:
любые.
,
,
.
Формула
разложения граничной функции в ряд по
сферическим гармоникам
имеет вид:
, (2.8.)
,
,
,
Из общего уравнения можно записать:
(2.9.)
Приравнивая при разложения (2.8.), (2.9.) получаем:
и решение задачи:
,
.
Основные характеристики излучателя находятся по стандартной методике:
,
,
,
,
,
,
,
.
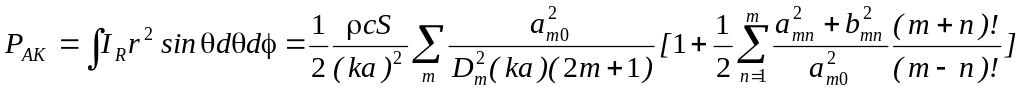Полное сопротивление излучения определяется методом ближнего поля через интегральную реакцию:
,
, 
.
При выводе формулы использовано соотношение:
.
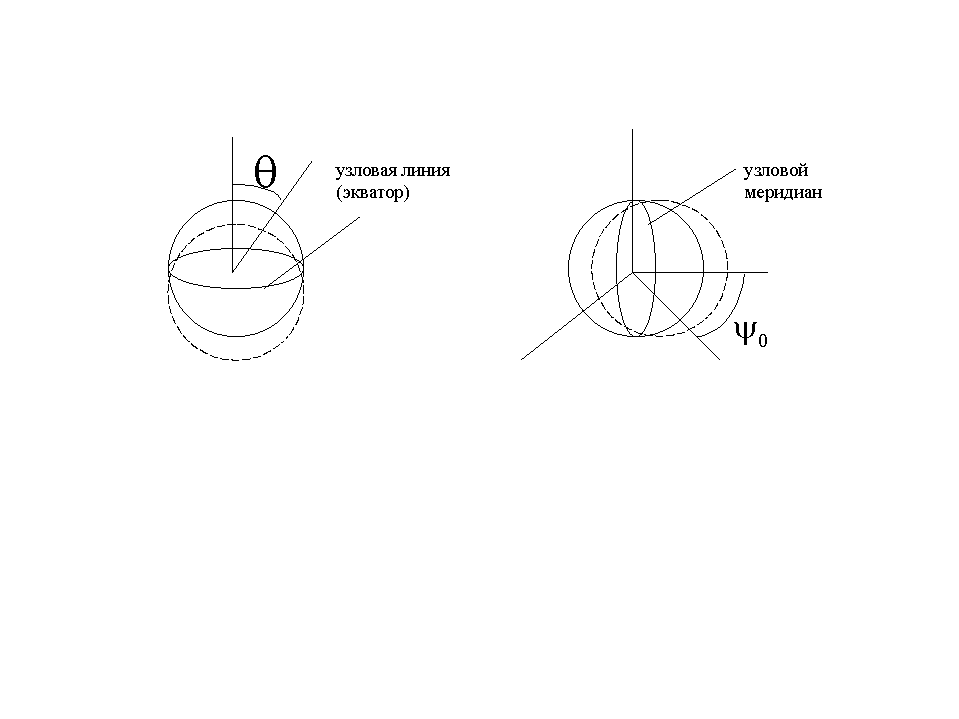
Физическая трактовка частных решений:
-
монополь,
,
.
Принята терминология:
-
зональные функции,
-
тессеральные (клетчатые) функции,
-
секториальные функции,
-
число узловых меридианов,
число узловых широт.
,
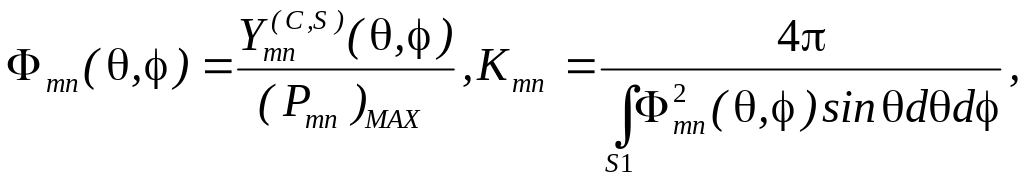
Эффективность
работы излучателя порядка
можно оценить величиной сопротивления
излучения
:
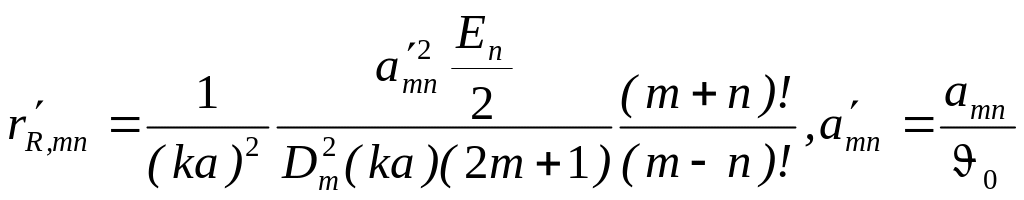при возбуждении излучателя функцией
,
.
В предельных случаях оценим:
,
, (2.9.)
,
,
Численные оценки по формулам (2.9.) сведены в таблицу.
На низких частотах эффективность излучателя определяется числом и ухудшается с ростом в силу эффекта акустического короткого замыкания.
На высоких
частотах излучатель любого порядка
создаёт одинаковый уровень излучения
в направлении максимума, однако,
излучатель порядка
затрачивает при этом в
раз меньшую мощность.
-
0
1
2
0
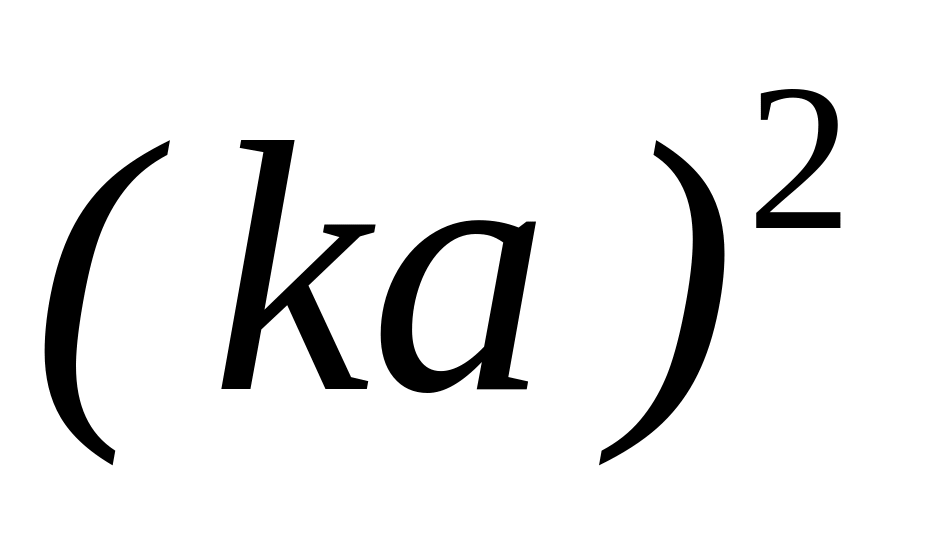
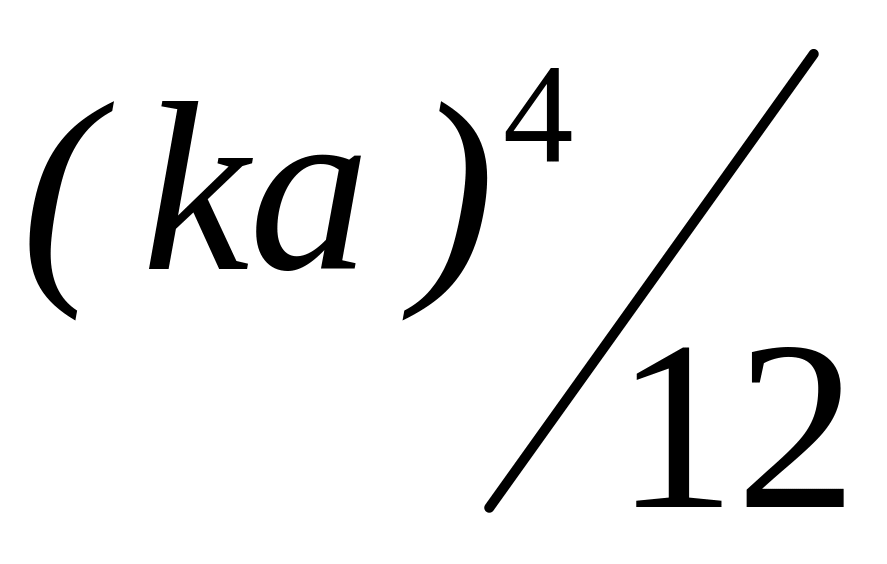
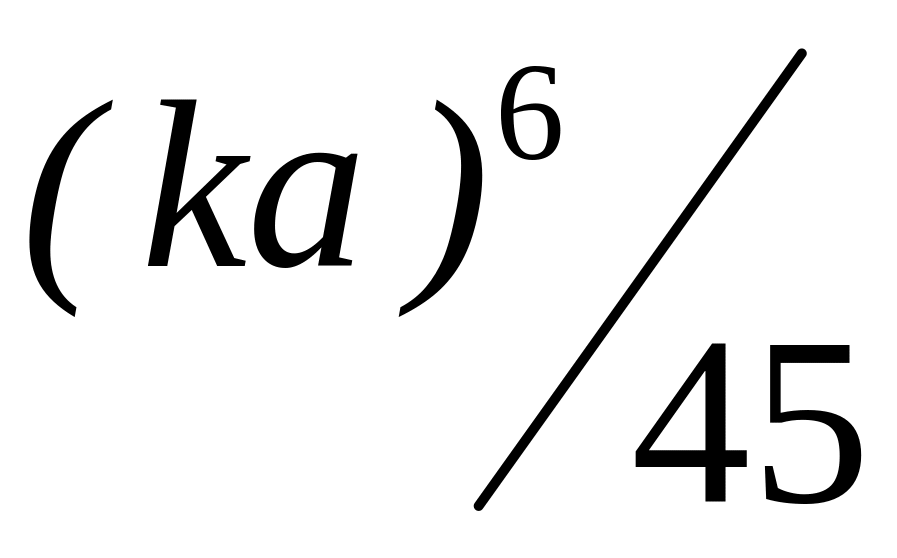
1
2
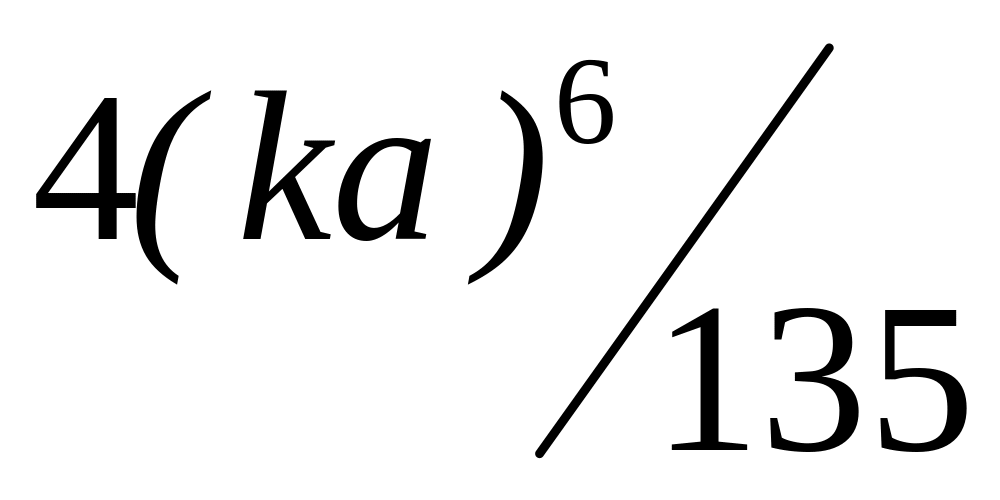
Модель сферического излучателя является достаточно универсальной и позволяет рассчитывать любые его характеристики при произвольном способе возбуждения. В сравнении с другими сферический излучатель при синфазном возбуждении работает наиболее эффективно, однако, технология его изготовления не является простой.
Наиболее близким аналогом являются излучатели, у которых активный (излучающий) элемент имеет форму круглого поршня или цилиндрического кольца, а сферическую или близкую к ней форму имеет только жёсткий экран. В связи с этим рассмотрим в качестве частных примеров следующие модели.
2.1.6. Малый поршневой излучатель
на поверхности жёсткой сферы.
,
,
,
,
,
,
,
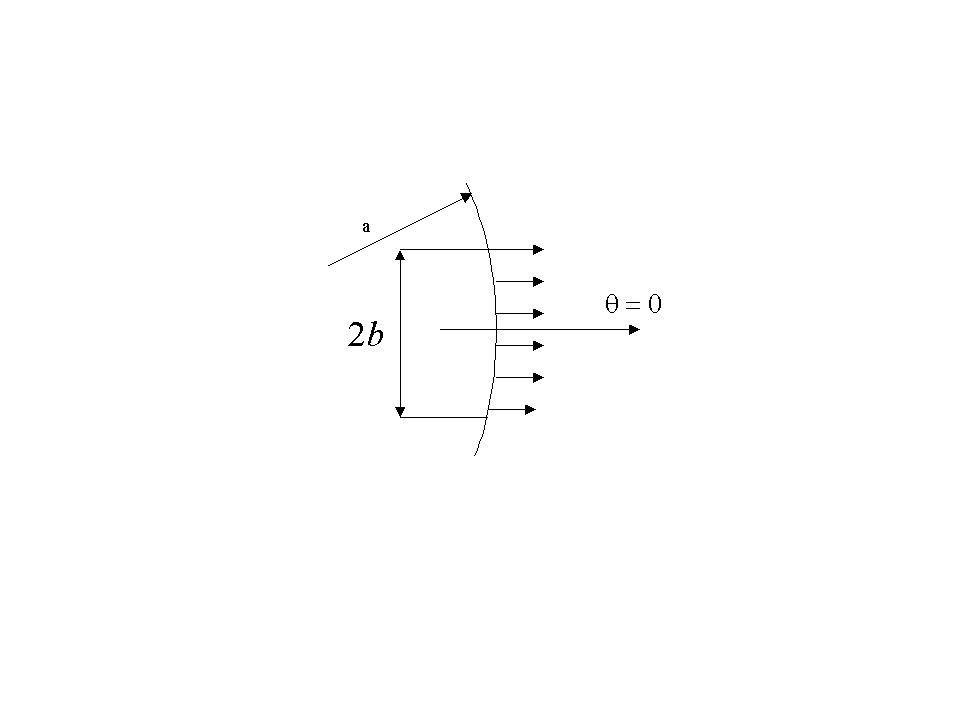
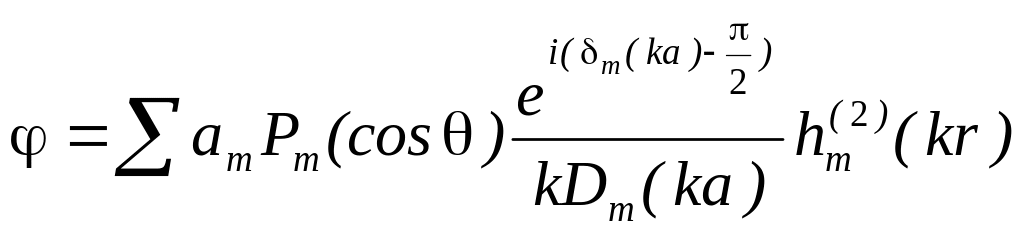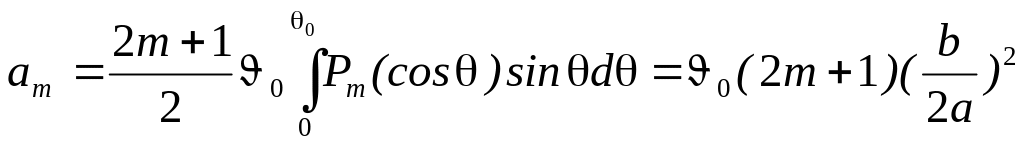, (2.10.)
-
площадь поршня.
Оценка (2.10.) является мерой эффективности работы такого излучателя, а его сопротивление излучения на низких частотах совпадает с аналогичной величиной односторонне излучающего поршня, который будет рассмотрен ниже.
2.1.7. Кольцевой излучатель
на поверхности жёсткой сферы.
,
,
,
,
,
,
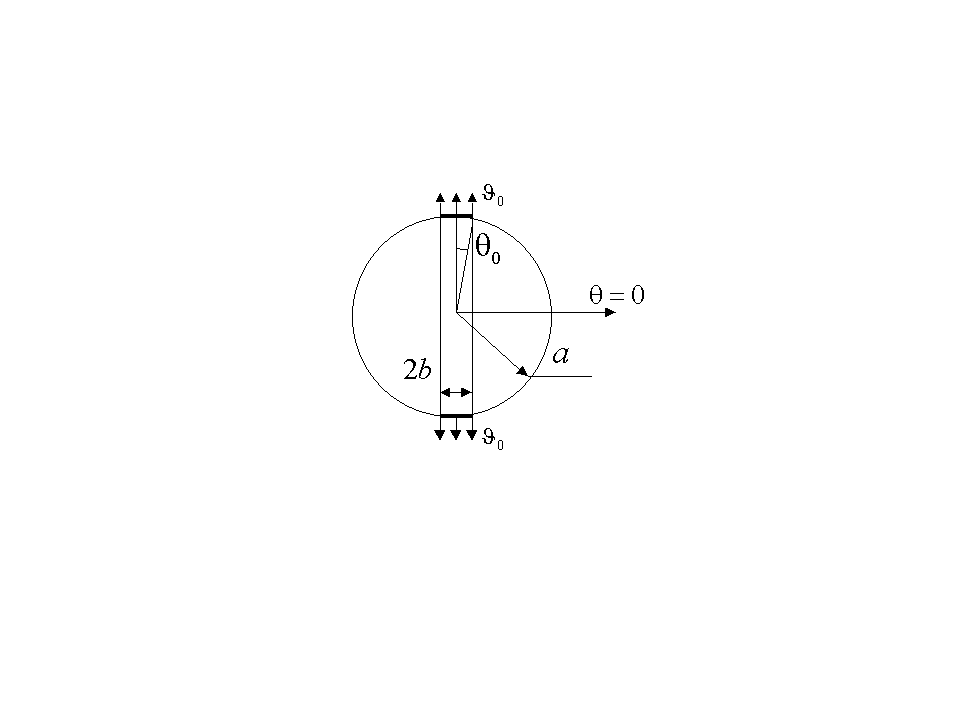
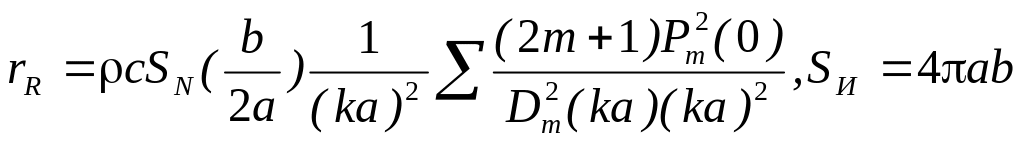. (2.11.)
2.1.8. Два малых поршня на поверхности
жёсткой сферы.
,
,
,
,
,
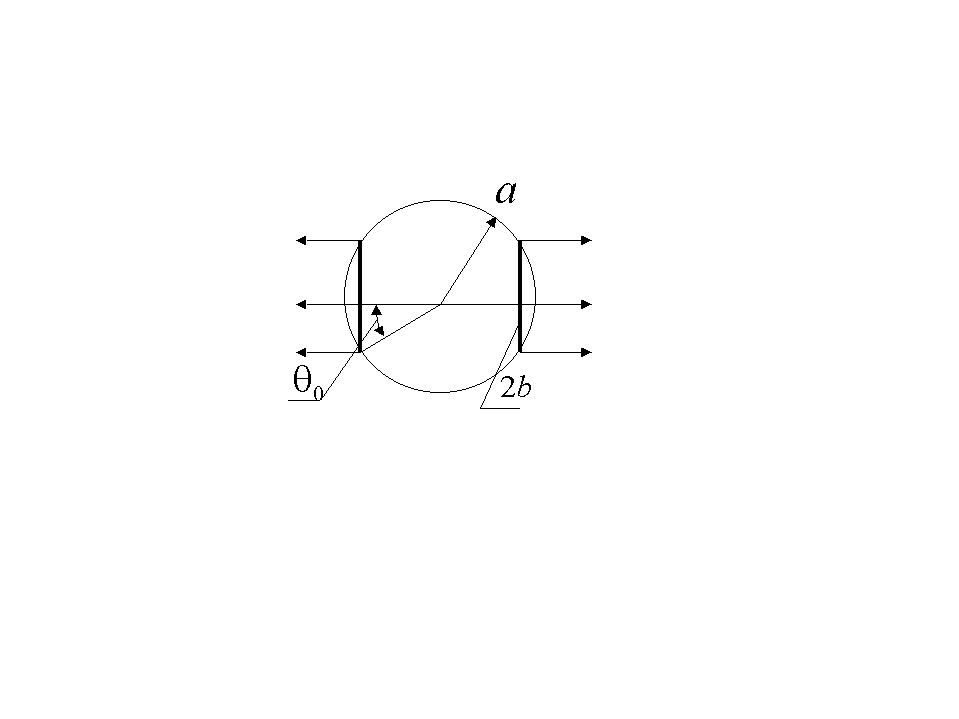
. (2.12.)
2.2. Цилиндрические излучатели.
Цилиндрические излучатели также относятся к числу модельных, а их геометрия соответствует широко распространённым цилиндрическим пьезоэлементам, используемым в качестве излучателей в среднечастотной гидроакустике. Теория цилиндрических излучателей строится в два этапа. На первом этапе модельный излучатель считается бесконечно протяжённым, а сама задача – двумерной. Полученные на этом этапе результаты имеют ограниченную применимость и в общем случае не соответствуют реальным условиям излучения.
На втором этапе учитывается конечная длина излучателя, а сама задача становится трёхмерной, т.е. соответствующей реальным условиям. Более простой и стандартный подход основан на использовании метода интегральных преобразований (метода неполного разделения переменных). В этом случае конечной считается длина собственно излучателя, который дополняется до бесконечно протяжённого жёстким экраном. Такого допущения достаточно для получения физически правдоподобных результатов, близких по существу к результатам, полученных другими методами.