
- •5.Классические решения простейших ду-ий с частными производными
- •6. Классификация линейных ду-ий 2-ого порядка со многими независимыми переменными
- •3.Приведение к канон. Виду д.У. Частн. Производ. 2го порядка с двумя независ. Перемен.
- •15. Схема метода разделения переменных для решения смешанных задач
- •16. Решение методом разделения переменных первой смешанной задачи для однор. Уравнения колебаний струны
- •21.Формулы Грина для оператора Лапласа
- •22. Свойства гармонических функций
- •17.Сведение смешанной задачи с неоднородными граничными условиями к задаче с однородными гр-ми усл-ми.
- •7. Привидение к каноническому виду ду частных производных 2-го порядка
- •8. Исключение младших производных в ду с частными производными второго порядка
- •4.Системы д.У в частн. Производн.
- •2.Классификация ду-ий в частных производных 2-ого порядка с двумя независимыми переменными.
- •11. Примеры некорректно поставленных задач Коши
- •Учитывая нач. Усл. (11.5), получаем соотношение
- •12.Задача Коши для уравнения колебаний струны
- •Производя замену переменных , ,
- •19. Постановка смешанных задач для уравнения теплопроводности.
- •20.Решение методом разделения переменных первой смешанной задачи для однор. Ур. Теплопроводности.
- •13. Постановка смешанных задач для уравнения колебаний струны
- •14. Задача Штурма-Лиувилля
- •18. Метод разделения пер-ых для решения смешанных задач с неоднородными ур-ми.
- •23.Краевые задачи для эллиптических уравнений.
11. Примеры некорректно поставленных задач Коши
1)Зад. Коши для гиперб. ур-ния с нач. усл. на хар-ке.
Рассм. зад. Коши:
 на
на
 (1)
(1)
( 2)
2)
где
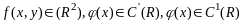 .
.
Предпол., что зад. Коши (1), (2) имеем
реш.
 ,
облад. непрер. смешанной произв.
,
облад. непрер. смешанной произв.
 в области
в области
 .
Т.к. линия
.
Т.к. линия
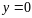 принадлежит области, то ДУ (1) должно
выполн.
на линии, т.е.
принадлежит области, то ДУ (1) должно
выполн.
на линии, т.е.
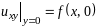 .
.
Учитывая второе условие (2), получ. необх. Усл. разрешимости зад. Коши (1), (2)
 .
(3)
.
(3)
Если усл. (3) не вып., то зад. (1), (2) не имеет решение.
Построим
реш. зад. Коши (1), (2), предполагая, что
усл. (3) выполнено. Воспольз. общим реш.
(5.2) ДУ (1), где ф-ции
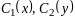 определим из начальных условий.
определим из начальных условий.
Из 1-го нач. усл. получим, что
 .
.
Положим
 .
.
Тогда второго нач. усл. получ. , что
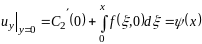 .
.
Учитывая
усл. разрешимости (3), получим соотношение
 .
Т.о. произв. ф-ция
.
Т.о. произв. ф-ция
 удовл. усл.
удовл. усл.
 ,
.
,
.
Общий вид такой функции
 ,
,
где
произвольная функция
 ,
,

Т.о., получено реш. зад. Коши (1), (2) в виде:
 ,
,
к-рое
не единственно в силу произвольности
функции
 .
.
В итоге приходипм к выводу, что задача Коши (1), (2) поставлена некорректно, т.к. не вып. 1-е или 2-е усл. корректности из опр. (10.2).
2)Зад. Коши для параболического уравн. с нач. усл. на хар-ке.
Рассмотрим задачу Коши
 на
,
(4)
на
,
(4)
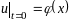 ,
,
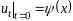 ,
,
 (5)
(5)
Предпол.,
что классич. реш. зад. (4), (5) сущ. для обл.
.
Т.к. линия
 принадл. данной обл., то ДУ (4) должно
выпол. и на линии, т.е.
принадл. данной обл., то ДУ (4) должно
выпол. и на линии, т.е.
 .
.
Учитывая нач. Усл. (11.5), получаем соотношение
 .
.
Это
усл. показ., что нач. ф-ция
 выражается через ф-цию
выражается через ф-цию
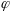 и коэф. ДУ (4), поэтому ф-ция
и коэф. ДУ (4), поэтому ф-ция
 не может быть произв.. Это означает, что
второе начальное условие (5) явл. лишним.
не может быть произв.. Это означает, что
второе начальное условие (5) явл. лишним.
В результате приходим к постановке задачи Коши для параболического уравн. с 1-м нач. усл. на хар-ке:
 на
на
(6)

в то время как задача Коши в постановке (4), (5) некорректно поставлена в случае произвольной функции .
3)Пример Адамара зад. Коши для эллиптического ур-ния.
Рассмотрим зад. Коши
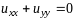 на
на
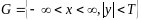 ,
(7)
,
(7)
 ,
,
 ,
,
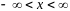 .
(8)
.
(8)
ДУ
(7) явл. ур-нием типа Коши-Ковалевской,
поэтому в случае аналитических ф-ций
и
на осн. теор. Коши-Ковалевской закл, что
задача (7), (8) имеет аналит реш. в некоторой
достаточно малой окр-сти линии
 .
Т.о., первые 2 усл. корректности выполнены
(локально). Иссл. 3-е условие корректности,
т.е. усл. о непрер. зав-ти от нач. ф-ций.
Для этого рассм. две задачи Коши с разл.
нач. усл. специального вида:
.
Т.о., первые 2 усл. корректности выполнены
(локально). Иссл. 3-е условие корректности,
т.е. усл. о непрер. зав-ти от нач. ф-ций.
Для этого рассм. две задачи Коши с разл.
нач. усл. специального вида:
 ,
,
 ,
,
 ,
,
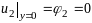 ,
(9)
,
(9)
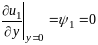 ,
,
 ,
,
где
 - фикс. положительный параметр.
- фикс. положительный параметр.
Решения данных задач определяются выражениями
 ,
,
 .
.
Введем
пространства функций
 ,
,
 ,
с соотв. метр. расст.:
,
с соотв. метр. расст.:
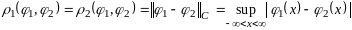 ,
,
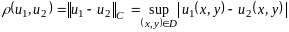 .
.
Согласно
опр. (10.2), применительно к задачам (9) и
(10), по
 ,
что если
,
что если
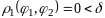 и
и
 (при
(при
 ),
тогда должно вып. нер-во
),
тогда должно вып. нер-во
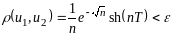 .
.
Очевидно,
что нер-во не выполнено при достаточно
больших знач. пар.
,
т.к.
 .
.
Т.о., задача Коши (7), (8) поставлена некорректно, т.к. не выполнено 3-е усл. корректности из опр. (10.2).
