25. Используя центральную предельную теорему, обоснуйте интегральную формулу Лапласа.

Интегральная приближенная формула Лапласа:

Пусть производится n независимых опытов, в каждом из которых с одной и той же вероятностью p наступает событие A. Рассмотрим случайную величину S_n –число наступлений события А в n опытах. Очевидно, S_n= X₁+ X₂+ …+ X_n, где Х_k обозначает число наступлений события А в k-ом опыте, k = 1, 2, …, n. Случайные величины Х_k имеют один и тот же закон распределения, так что они удовлетворяют условию Ляпунова. Тогда

. (1)

Это равенство носит название интегральной предельной теоремы Лапласа. Из него следует интегральная приближенная формула Лапласа:

Событие равнозначно условию . Положим k₁= , k₂= , так что .

Теперь левую часть формулы (1) можно записать в виде:

, правую: , где Ф(х) – функция Лапласа, которую можно представить как . Приравнивая выражение, стоящее под знаком предела к данному, получаем приближенное равенство

.

26. Докажите, что для генерального распределения с математическим ожиданием m и конечной дисперсией σ2 выборочное среднее является несмещенной и состоятельной оценкой m.

Выборочное среднее ¯x=1/n*Σx_n является несмещённой состоятельной оценкой математического ожидания m.

Арифметическая средняя , вычисленная по n независимым наблюдениям над случайной величиной x, которая имеет математическое ожидание Mx = m, является несмещенной оценкой этого параметра.

Док-во:

Пусть - n независимых наблюдений над случайной величиной x. По условию Mx = m, а т.к. являются случайными величинами и имеют тот же закон распределения, то тогда . По определению средняя арифметическая

.

Рассмотрим математическое ожидание средней арифметической. Используя свойство математического ожидания, имеем:

,

т.е. . является несмещенной оценкой.

Арифметическая средняя , вычисленная по n независимым наблюдениям над случайной величиной x, которая имеет Mx = m и , является состоятельной оценкой этого параметра.

Док-во:

Пусть - n независимых наблюдений над случайной величиной x. Тогда имеем Mx = .

Для средней арифметической запишем неравенство Чебышева:

.

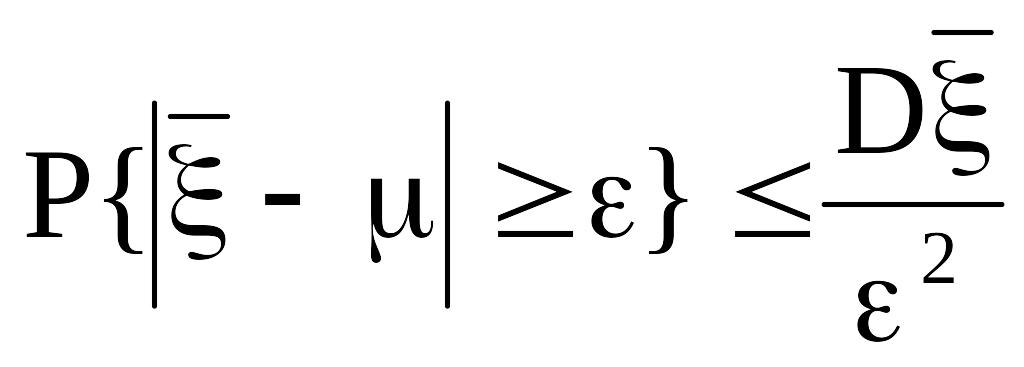Используя свойства дисперсии имеем:

,

т.к. по условию теоремы .

Следовательно,

Итак, дисперсия средней арифметической в n раз меньше дисперсии случайной величины x. Тогда

,

поэтому

,

а это значит, что является состоятельной оценкой.

27. Пусть x1,…Xn – выборка из распределения с дисперсией 2. Док-те, что - несмещенная оценка 2.

Пусть Zn = (x₁…x_n) – случ выборка объема n, тогда исправленной выборочной дисперсией называется величина s²=n/(n-1) . Следствие: S² – несмещенная оценка ².

M(S²)=M(n/(n-1) ) = n/(n-1) M( ) = n/(n-1) * (n-1)/n * ² = ², т.к.

M( )= .

28. Выведите формулу для дисперсии выборочного среднего бесповторной выборки.

В случае простой бесповторной выборки x₁…x_n мат ожидание и дисперсия выборочного среднего опр по формулам M( )=m D( )=²/n * (N-n)/(N-1).

Док-во: 1) M( ) = M ((x₁+…+x_n)/n) = 1/n (m+…+m)=m.

2)D((x₁+…+x_n)/n)=1/n² * D(x₁+…+x_n) = 1/n² * {D(x₁)+...+D(x_n) + 2 } = 1/n² (n²+2C²_n*C)=

= 1/n² (n²+2*{n(n-1)/2}*C)=1/n (²+(n-1)C) ====

Рассм. случ выборку, сост из элементов ген совокупности (n=N), тогда - не случ величина, а константа, сл-но, при n=N D( )=0=1/N (²+(N-1)C), сл-но, C = -²/(N-1)

==== 1/n (²+(n-1)* {-²/(N-1)}) = …