Машина Тьюринга.

Машина Тьюринга. Описание, способы задания, особенности программирования машин Тьюринга (МТ). Основные операции над МТ, доказательство теоремы о существовании универсальной МТ. Примеры.

Алан Тьюринг (Turing) в 1936 году опубликовал в трудах Лондонского математического общества статью, где для уточнения понятия алгоритма был предложен абстрактный универсальный исполнитель. Эта работа наравне с работами Поста и Черча лежит в основе современной теории алгоритмов.

Предыстория её создания связана с формулировкой списка из 23 кардинальных проблем математики, представленного Давидом Гильбертом на II Международном Конгрессе математиков в Париже в 1900 году.

Характеристика, данная работе Тьюринга Джоном Хопкрофтом: «Тьюрингу пришлось дать четкое определение самого понятия метода. Отталкиваясь от интуитивного представления о методе как о некоем алгоритме, т.е. процедуре, которая может быть выполнена механически, без творческого вмешательства, он показал, как эту идею можно воплотить в виде подробной модели вычислительного процесса. Полученная модель вычислений, в которой каждый алгоритм разбивался на последовательность простых, элементарных шагов, и была логической конструкцией, названной впоследствии машиной Тьюринга». (с16)

Машина Тьюринга является расширением модели конечного автомата, расширением, включающим потенциально бесконечную память с возможностью перехода (движения) от обозреваемой в данный момент ячейки к ее левому или правому соседу.

Неформально, машина Тьюринга (далее МТ) представляет собой автомат с конечным числом состояний и неограниченной памятью, представленной бесконечной лентой. Лента поделена на бесконечное число ячеек, и на ней выделена стартовая ячейка.

В каждой ячейке ленты может быть записан только один символ из некоторого конечного алфавита, где также предусмотрен символ для обозначения пустой ячейки.

С лентой взаимодействует головка чтения-записи, которой управляет «управляющее устройство» МТ — автомат с конечным множеством состояний.

Имеется выделенное стартовое состояние и состояние завершения.

Перед запуском МТ находится в начальном состоянии, а головка позиционируется на пустой ячейке ленты.

На каждом шаге головка считывает информацию из текущей ячейки, и посылают ее управляющему устройству МТ. В зависимости от этих символов и собственного состояния, управляющий устройство может производить следующие операции:

• записывать символ алфавита в ячейку (в том числе и пустой), заменяя находившийся в ней (в том числе и пустой);

• передвигать головку на одну ячейку влево, вправо или остается на месте;

• менять свое внутреннее состояние; (с18)

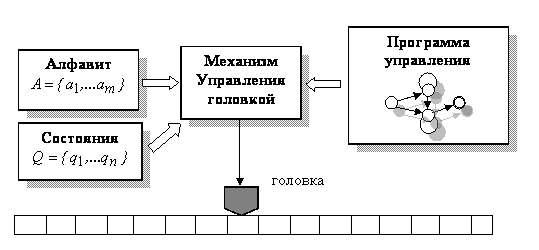
Рис.2 Машина Тьюринга

Формально машина Тьюринга может быть описана следующим образом (с19):

• конечное множество состояний – Q = {q₀, q₁, ..., q_n}, в которых может находиться машина Тьюринга, называемое внутренним алфавитом;

• конечное множество символов ленты – А = {a₀, а₁, ...,а_t} называемое внешним алфавитом;

• функция (функция переходов или программа), которая задает отображение пары из декартова произведения Q x А (машина находится в состоянии и обозревает символ a_k) в тройку декартова произведения Q х А х {L,R,E} (машина переходит в состояние q_j, заменяет символ a_k на символ a_m и передвигается влево, вправо на один символ ленты или остается на месте) – Q x А-->Q х А х {L,R,E}: . Предполагается, что для каждой пары q_ia_k, i=1,…n, k=0,…t имеется точно одна команда. Множество этих команд называется программой и в программе имеется n(t+1) команд;

• один символ (пустой);

• подмножество определяется как подмножество входных символов ленты, причем ; т.е. в начальный момент на ленте имеется конечное число непустых символов.

• одно из состояний – является начальным состоянием машины, а заключительным.

Обязательно требование детерминизма, т.е. не должно быть команд с одинаковой левой частью.

Должна быть команда, в правой части которой есть заключительное состояние.

Для МТ ниоткуда не следует, что начав работать из начального состояния, она когда-нибудь выйдет на заключительное состояние. Вводить это требование не получается, т.к. по описанию нельзя заранее предугадать эту ситуацию.

Способы задания МТ:

Список команд (с20)

Таблица переходов (с20)

Граф переходов. (с21)

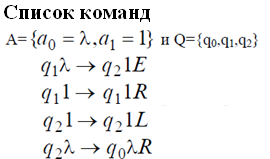
Таблица переходов

МТ можно описать в виде таблицы, где строки соответствуют состояниям, а столбцы символам внешнего алфавита. Данное представление автоматически обеспечивает детерминизм и удобно тем, что видно, что задали все возможные команды, т.е. для любой левой части есть правая.

	a0	a1
q1	q2a1E	q1a1R
q2	q0a0R	q2a1L
q0	…	…

Граф переходов

Этот граф является ориентированным и строится следующим образом: вершины графа соответствуют состояниям МТ, дуга ведет из одного состояния в другое и подписывается, согласно правилу перехода из одного состояния в другое без указания самого состояния (рис.3).

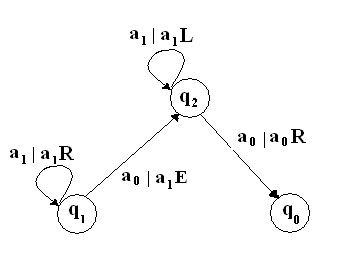
Рис.3

Чтобы задать конкретную машину Тьюринга, требуется описать для нее следующие составляющие:

Внешний алфавит. Конечное множество, элементы которого называются буквами (символами). Одна из букв этого алфавита должна представлять собой пустой символ.

Внутренний алфавит. Конечное множество состояний управляющего устройства. Одно из состояний (например, q1) должно быть начальным (запускающим программу). Еще одно из состояний (q0) должно быть конечным (завершающим программу) – состояние останова.

Систему команд тем или иным способом.

(с22-с23)

Далее условимся отдельные символы алфавита обозначать латинскими буквами, а слова греческими.

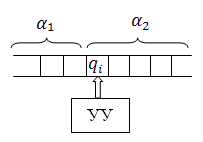
Машина обозревает первый символ слова и слева написано слово МТ находится в состоянии q_i.

Детерминизм МТ заключается в том, что всякая конфигурация однозначно определяет следующую конфигурацию.

Эта последовательность называется протоколом.

Если в протоколе какая-либо конфигурация повториться, то машина зациклится.

K₀→K₁→…→ K_i →K_i+1 →…→K_i →K_i+1→…

Иными словами, если МТ выдает результат, т.е. останавливается, то ни одна конфигурация в её протоколе не повторяется.

Стандартная начальная конфигурация имеет вид (т.е. МТ всегда, в начале, обозревает крайний левый символ), а стандартная заключительная (это означает, что в момент остановки на ленте нет мусора, все промежуточные результаты стерты).

Когда вид начальной конфигурации совпадает с видом заключительной конфигурации легко предавать управление от одной МТ к другой, т.е. начинать новые вычисления.

Этого всегда можно добиться, т.е. привести заключительную конфигурацию к стандартному виду используя следующий прием: (с24)

добавим к МТ два новых состояния q^` q`` и команды

МТ^` эквивалентна МТ в следующем смысле:

Лемма 1. Для всякой МТ Т можно построить эквивалентную МТ Т^/, у которой все заключительные конфигурации стандартны.

Определение вычислимости по Тьюрингу. (с25)

Введя понятие алгоритма как МТ, можно сформулировать понятие вычислимости в этих терминах.

С каждой МТ можно связать некоторую функцию. Понятие вычислимости нетривиально. Функцию можно задать, но не знать алгоритма её вычисления. Функция вычислима если существует алгоритм, который её вычисляет и невычислима если алгоритма не существует.

Будем рассматривать функции f следующего типа f: A^* →A^*, где А^* - множество всех слов конечной длины в алфавите A.

Говорят, что МТ вычисляет функцию f_мт, если для любого выполнено:

Функция f называется вычислимой по Тьюрингу, если существует МТ которая её правильно вычисляет.

Скажем, что две МТ Т₁ и Т₂ эквивалентны, если они вычисляют одинаковые функции.

(с26)

Будем считать, что алфавит А МТ содержит 1.

МТ правильно вычисляет функцию , если

Примеры (с27-с29)

Рассмотрим несколько примеров построения МТ.

I

II

III

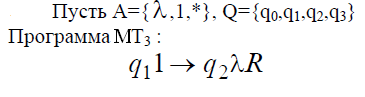
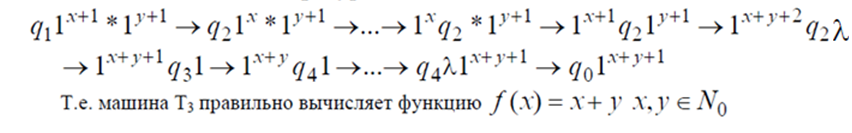
Каждая МТ может вычислять только одну функцию.

Для решения более сложных задач используются различные способы сочетания нескольких МТ, т.е. задаются операции над МТ.

Операции над двумя МТ.

Последовательная композиция МТ. (с30-с31)

Пусть даны две машины Тьюринга Т₁ и Т_2, которые вычисляют соответствующие функции в одном и том же алфавите. Тогда существует машина Тьюринга Т, которая вычисляет функцию . При этом для любого слова функция определена в том и только в том случае, когда определена и определена.

Параллельная композиция. Пусть м.Т. вычисляет функцию f(x), а м.Т. - функцию g(x) и символ * не входит в алфавит м.Т. . Тогда существует м.Т. которая по любому входу вида x*y выдает результат f(x)*g(y), т.е. вычисляет функцию H(x*y) = f(x)*g(y).

Операция ветвления (условный оператор).(с32-с33)

Пусть даны две машины Тьюринга Т₁ и Т_2, которые вычисляют соответствующие функции в одном и том же алфавите.

Тогда существует машина Тьюринга Т, которая вычисляет функцию определенную следующим образом

Т.е. нужно уметь вычислять предикат , а значит построить машину Тьюринга Т_p вычисляющую предикат. Вычислять можно двумя способами.

Первый вариант заменить на ленте на 0 или 1, но это очень часто сделать нельзя, т.к. необходимо сохранить входное слово . Поэтому существует второй вариант, так называемое вычисление с восстановлением, дающее в заключительной стандартной конфигурации q₀^p .

Тогда машина Тьюринга Т начальную конфигурацию

Существование машины Т вытекает из следующих конструкций.

Строится МТ Т_p вычисляющая предикат с восстановлением.

Строится промежуточная машина Т₃ с начальным состоянием и системой команд

}

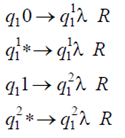где команды машины Т₁, а машины Т₂ соответственно.

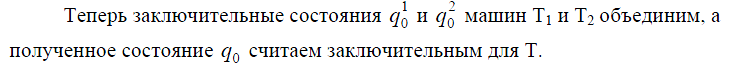Тогда Т( ) – это композиция двух машин Т₃(Т_p( )).

Реализация цикла.(с34)

Универсальная машина Тьюринга.

Машины, которые строились до сих пор, были специализированными. Поскольку каждая МТ вычисляет только одну функцию, встает вопрос: можно ли построить такую машину, которая имитирует поведение любой другой машины?

На самом деле это означает следующий вопрос: можно ли не строить каждый раз отдельные машины, а производить все вычисления на одной машине? Сам Тьюринг назвал это моделированием.

Доказывается теорема о существовании универсальной МТ.

В такой машине входное слово должно включать изображение программы и входное слово интерпретируемой машины.

Теорема: Построение универсальной МТ.(с35)

Пусть Т₁(α)-∑₁, Т₂(α)- ∑₂,… Т_n(α)-∑_n … - машины Тьюринга и их системы команд, можно ли построить такую машину T_u(α, ∑_Ti) = Т_i(α), т.е. на ленте записываем не только аргумент машины Т_i, но и систему команд этой машины.

Доказательство этой теоремы конструктивное.

Чтобы получить изображение программы интерпретируемой машины, нужно последовательно, строка за строкой, закодировать эту программу в алфавите универсальной машины. Универсальная машина Тьюринга должна иметь фиксированный внешний алфавит, используемый при записи программы (системы команд), включая и алфавит интерпретируемой машины.

Поэтому ∑_Ti - это не просто система команд машины Т_i, а это некоторый её код в алфавите машины T_u.

Идея алгоритма универсальной машины: сканировать любую систему команд, находить нужную левую часть, выполнять правую часть и снова сканировать.

Лента делится на часть содержащую систему команд и часть с данными.

По ходу этой реализации доказываются некоторые дополнительные утверждения.

Например, лента может быть бесконечной в одну сторону (односторонняя МТ). Для всякой МТ можно построить эквивалентную одностороннюю МТ.

Таким образом, в этой теореме о существовании универсальной машины заложены все основные фундаментальные идеи вычислительной техники.

Идея существования универсальной машины.

Идея, что в конкретном алфавите можно закодировать любой алгоритм (программа на языке программирования)

Любой сколь угодно сложный алгоритм можно реализовать на машине с конечной памятью, т.е. все компьютеры (независимо от мощности, архитектуры и т.д.) эквивалентны с точки зрения принципиальной возможности решения алгоритмических задач.

Идея вычислительной машины не инженерная, а математическая (строго доказанная).

Тезис Тьюринга - принимаемое без доказательства фундаментальное положение теории алгоритмов, согласно которому всякий алгоритм представим в форме машины Тьюринга.

Тезис Тьюринга: Если функция вычислима, то существует машина Тьюринга, которая её вычисляет.

На основе этого тезиса можно теперь доказывать, что в некоторых случаях алгоритмов не существует.

Алгоритмически неразрешимые задачи (с36)

Формализация понятия алгоритма позволила исследовать существование задач, для которых не существует алгоритмов поиска решений.

Алгоритм можно представить себе как некоторый "черный ящик", на вход которого подаются данные и на выходе получается некоторый результат. Другими словами, можно назвать алгоритм функцией, преобразующей данные в результат.

Вычислимая функция - это функция, для вычисления которой существует алгоритм. Любая вычислимая функция может задаваться разными алгоритмами (разными программами для выбранного универсального исполнителя). Любая вычислимая функция может быть вычислена с помощью любого универсального исполнителя: машин Тьюринга и Поста, нормальных алгорифмов Маркова и др.

Существуют и невычислимые функции.

Пример:

Известно, что математическая постоянная π — иррациональное число, его десятичная запись бесконечна и не периодична. Введем функцию h(n), которая для любого натурального числа n равна 1, если в десятичной записи числа π есть n стоящих подряд девяток, окруженных другими цифрами, и равна нулю, если такой цепочки девяток нет. Как вычислить значение этой функции при некотором заданном n?

Конечно, можно вычислять друг за другом десятичные знаки числа π (такие алгоритмы математикам известны!) и проверять, не нашлась ли в полученной последовательности цифр цепочка из n девяток. С помощью такого "наивного” алгоритма можно найти такие значения n, при которых h(n) = 1: обнаружив требуемую цепочку, алгоритм закончит работу. Например, анализ первых 800 знаков показывает, что h(n) = 1 при n = 0, 1, 2, 6. Но если для какого-то n функция h(n) равна нулю, то наивный алгоритм никогда не остановится. Более того, для этой функции вообще не существует алгоритма, который при любом n останавливается и выдает значение h(n) в качестве результата. Поэтому такая функция невычислима.

В математике и информатике существуют задачи, для которых общее решение не только неизвестно сейчас, но и вообще отсутствует. Поэтому искать его бесполезно.

Одним из свойств алгоритма является его массовость. Это означает, что алгоритм представляет собой способ решения некоторой массовой проблемы, формулируемой в виде проблемы отображения не одного, а целого множества входных слов в соответствующие им выходные слова.

Важно точно указывать допустимое множество входных данных, поскольку задача может быть решаемой для одного множества и неразрешимой для другого.

Таким образом, всякий алгоритм можно рассматривать как некоторое универсальное средство для решения целого класса задач.

Оказывается, что существуют такие классы задач, для решения которых, нет и не может быть единого универсального приема. Проблемы решения такого рода задач называют алгоритмически неразрешимыми проблемами. Однако алгоритмическая неразрешимость задачи того или иного класса вовсе не означает невозможность решения любой конкретной задачи из этого класса. Речь идет о невозможности решения всех задач данного класса одним и тем же приемом.

Одной из первых задач, для которой была доказана неразрешимость, является проблема остановки.

Проблема останова МТ:

Даны описание алгоритма и его начальные входные данные, требуется определить, сможет ли выполнение алгоритма с этими данными завершиться когда-либо. Альтернативой этому является то, что он работает всё время без остановки.

Алан Тьюринг доказал в 1936 году, что не существует общего алгоритма для решения проблемы остановки. Другими словами, проблема остановки неразрешима на машине Тьюринга.

Таким образом, фундаментально алгоритмическая неразрешимость связана с бесконечностью выполняемых алгоритмом действий, т.е. невозможностью предсказать, что для любых исходных данных решение будет получено за конечное количество шагов.

Доказательство неразрешимости проблемы остановки важно тем, что к ней можно свести другие задачи.

Доказательство неразрешимости проблемы остановки (из википедии)

Рассмотрим множество алгоритмов, которые принимают на вход натуральное число и на выходе тоже выдают натуральное число. Каждый алгоритм можно записать в виде конечной последовательности символов внешнего алфавита некоторой универсальной МТ. Упорядочим множество лексикографически (в словарном порядке), при этом каждый алгоритм получит свой порядковый номер. F алгоритм решающий проблему остановки, который получает на вход пару натуральных чисел , и:

останавливается и возвращает 1, если алгоритм с номером не останавливается, получив на вход

не останавливается в противном случае (если алгоритм с номером останавливается, получив на вход ).

Докажем, что F не существует.

Доказательство от противного. Допустим, F существует. Напишем алгоритм F₁, который принимает на вход число , передает пару аргументов F и возвращает результат его работы. Другими словами, F₁ останавливается в том и только том случае, если не останавливается алгоритм с номером , получив на вход число . Пусть - это порядковый номер F₁ в множестве . Запустим F₁, передав ему это число . F₁ остановится в том и только том случае, если алгоритм с номером (то есть, он сам) не останавливается, получив на вход число (какое мы ему и передали). Из этого противоречия следует, что наше предположение неверно: F не существует, что и требовалось доказать.

Пример: Вычисление совершенных чисел;

Совершенные числа – это числа, которые равны сумме своих делителей, например: 28 = 1+2+4+7+14.

Определим функцию S(n) = n-ое по счёту совершенное число и поставим задачу вычисления S(n) по произвольно заданному n. Нет общего метода вы-числения совершенных чисел, мы даже не знаем, множество совершенных чи-сел конечно или счетно, поэтому наш алгоритм должен перебирать все числа подряд, проверяя их на совершенность. Отсутствие общего метода решения не позволяет ответить на вопрос об останове алгоритма. Если мы проверили М чисел при поиске n-ого совершенного числа – означает ли это, что его вообще не существует?

Методы доказательства алгоритмической неразрешимости

Существуют два метода доказательства неразрешимости.

Первый, прямой метод, состоит в том, что используя диагональную процедуру, из предположения о разрешимости данной проблемы мы приходим к противоречию.

Второй, косвенный метод состоит в следующем. Показывается, что разрешимость исследуемой проблемы влечёт разрешимость проблемы, о которой уже известно, что она неразрешима. Метод сведения часто бывает более удобным, чем прямой метод.

Применяя метод сведения, обычно ссылаются на искусственные задачи, которые не представляют самостоятельного интереса, но для которых легко непосредственно доказать их неразрешимость.

Пример

Самопримени́мость в теории алгоритмов — свойство алгоритма успешно завершаться на данных, представляющих собой формальную запись этого же алгоритма.

Задача распознавания самоприменимости является алгоритмически неразрешимой и сводится к тому, чтобы найти алгоритм, позволяющий за конечное число шагов по формальной записи некоего алгоритма узнать, является ли он самоприменимым или нет. Хотя эта задача несколько искусственна и не представляет самостоятельного интереса, но часто используется для того, чтобы доказать неразрешимость других, более сложных задач. Общий метод для подобных выводов состоит в том, что из предположения о существовании алгоритма, решающего некую задачу, выводится существование алгоритма, решающего задачу распознавания самоприменимости.

Лекция №3.

Введение в теорию рекурсивных функций. Определения, примеры, способы задания рекурсивных функций, формулировка и доказательство соответствующих теорем.