1. Электрический заряд. Дискретность заряда. Закон сохранения электрического заряда.

2. Закон Кулона. Принцип суперпозиции.

3. Напряженность электрического поля. Линии напряженности электрического поля. Принцип суперпозиции.

4. Напряженность электростатического поля тонкого заряженного стержня, тонкого заряженного кольца, плоского заряженного кольца и диска.

5. Напpяженность электростатического поля системы точечных зарядов. Электрический диполь и его поле.

6. Силовые линии поля. Поток вектора.

7. Электростатическая теорема Гаусса и ее применение для расчета полей.

8. Работа электростатического поля. Циркуляция напряженности поля. Теорема о циркуляции.

9. Потенциал. Принцип суперпозиции. Энергия электростатического поля.

10. Потенциал электростатического поля тонкого заряженного стержня, тонкого заряженного кольца, плоского заряженного кольца и диска.

11. Разность потенциалов. Связь потенциала с напряженностью электростатического поля.

12. Проводники. Равновесие зарядов на проводнике.

13. Поверхностная плотность заряда. Граничные условия на границе проводника с вакуумом.

14. Общая задача электростатики. Уравнение Пуассона.

15. Емкость уединенного проводника.

16. Конденсаторы. Емкость конденсатора.

17. Емкость конденсаторов различной конфигурации.

18. Соединение конденсаторов.

19. Энергия взаимодействия электрических зарядов.

20. Энергия уединенного проводника.

21. Энергия конденсатора. Плотность энергии электростатического поля.

22. Диполь во внешнем электрическом поле.

23. Поляризация диэлектриков. Поляризационные заряды. Вектор поляризации.

24. Теорема Гаусса для диэлектриков. Электрическое смещение.

25. Условия на границе раздела диэлектрика с диэлектриком.

26. Плоский конденсатор с диэлектриком. Плотность энергии электрического поля в диэлектриках.

27. Электрический ток. Плотность тока. Условия существования тока.

28. Законы Ома и Джоуля-Ленца в дифференциальной форме.

29. Сторонние силы. Электродвижущая сила.

30. Законы Ома и Джоуля-Ленца в интегральной форме.

31. Правила Кирхгофа и расчет электрических цепей.

32. Вектор магнитной индукции. Принцип суперпозиции. Линии индукции магнитного поля.

33. Сила Лоренца и сила Ампера.

34. Закон Био-Савара-Лапласа.

35. Магнитное поле прямолинейного тока, в центре и на оси кругового тока.

36. Теорема Гаусса для магнитных полей.

37. Теорема о циркуляции магнитного поля. Магнитное поле соленоида.

38. Виток с током в магнитном поле. Момент сил, действующих на виток.

39. Работа, совершаемая при перемещении витка с током в магнитном поле.

40. Движение заряженных частиц в магнитном поле. Удельный заряд частицы.

41. Эффект Холла.

42. Явление электромагнитной индукции. ЭДС индукции, возникающая в движущихся проводниках.

43. Закон электромагнитной индукции. Правило Ленца.

44. Самоиндукция. Индуктивность. Индуктивность длинного соленоида.

45. Электрический ток при замыкании и размыкании цепи.

46. Магнитная энергия тока. Объемная плотность энергии магнитного поля.

47. Строение атомов и молекул. Намагничивание вещества.

48. Молекулярные токи. Намагниченность.

49. Теорема о циркуляции магнитного поля в веществе. Напряженность магнитного поля.

50. Магнитная восприимчивость и магнитная проницаемость. Граничные условия в магнитостатике.

51. Диамагнетики. Элементарная теория диамагнетизма.

52. Парамагнетики. Элементарная теория парамагнетизма.

53. Ферромагнетики. Основы теории ферромагнетизма. Гистерезис.

54. Фарадеевская и максвелловская трактовки явления электромагнитной индукции.

55. Ток смещения. Обобщение теоремы о циркуляции магнитного поля на случай переменных полей.

56. Система уравнений Максвелла в интегральной и дифференциальной формах.

57. Скорость распространения электромагнитных возмущений.

58. Квазистационарные токи в линейных проводниках.

59. Процессы установления тока при зарядке и разрядке конденсатора.

60. Колебательный контур. Затухающие электромагнитные колебания в колебательном контуре.

61. Условный период затухания колебаний. Коэффициент затухания и логарифмический декремент затухания колебаний.

62. Генератор переменного тока.

63. Вынужденные электромагнитные колебания в колебательном контуре. Резонанс в цепи с гармоническими токами.

64. Трансформатор.

65. Цепи переменного тока. Закон Ома для переменного тока. Импеданс.

66. Работа и мощность переменного тока. Действующие значения тока и напряжения.

67. Волновое уравнение. Плоские электромагнитные волны.

68. Энергия и импульс электромагнитной волны. Вектоp Умова-Пойтинга.

69. Излучение диполя.

1.

Электри́ческий заря́д — это физическая скалярная величина, определяющая способность тел быть источником электромагнитных полей и принимать участие в электромагнитном взаимодействии. Впервые электрический заряд был введён в законе Кулона в 1785 году.

Единица измерения заряда в СИ — кулон — электрический заряд, проходящий через поперечное сечение проводника при силе тока 1 А за время 1 с. Заряд в один кулон очень велик. Если бы два носителя заряда (q₁ = q₂ = 1 Кл) расположили в вакууме на расстоянии 1 м, то они взаимодействовали бы с силой 9·10⁹ H, т.е. с силой, с которой гравитация Земли притягивала бы предмет с массой порядка 1 миллиона тонн.

Уравнение состояния газа основано на атомной структуре вещества. Справедливость его является простейшим и важнейшим доказательством того, что структура вещества дискретная. Покажем, что атомная структура вещества в сочетании с закономерностями электролиза однозначно приводит к заключению о дискретности электрического заряда.

Явление электролиза, открытое Фарадеем, заключается в том, что растворы электролитов (солей, кислот и щелочей) при прохождении через них электрического тока химически разлагаются на составные части. При этом оказывается, что количество вещества МА, выделяемого на электроде, пропорционально атомной массе вещества А и количеству прошедшего электричества Q. Если заряд равен вполне определенной величине, а именно 96496 кулонам (эта величина называется постоянной Фарадея и обозначается через F) и на электроде выделяется одновалентное вещество, то его количество равно одному молю. Атомы в электролите несут на себе заряды (их называют ионами), а так как в одном моле содержится N0 атомов, т. е. столько же ионов, то чтобы через электролит прошел заряд F, необходимо, чтобы заряд иона равнялся F/N0. Эта величина F обозначается так: е — -дт- и равна 1,6021892 * 10“19 Кл. Если выделяемое вещество имеет валентность Z, то при прохождении заряда F на электроде выделится не один моль вещества, а в Z раз меньше (это количество вещества называют молярной массой эквивалента). Отсюда можно заключить, что заряд иона вещества с валентностью Z будет равен Ze.

Таким образом, величина е (точнее ±е) представляет собой наименьшую порцию электричества или элементарный заряд.

В общем виде закон Фарадея для количества вещества Мд в граммах можно выразить следующим образом:

При прохождении тока ионы электролита, подходя к металлическим электродам, не могут двигаться в металлической части цепи тока — они выделяются- на электродах в виде нейтральных атомов, заряд же их переносится внутри металлических частей цепи другими частицами — электронами, имеющимися и свободно передвигающимися в металле. Частицы эти имеют заряд — е и массу те = 9,109534 • 10~31 кг. Из электронов состоят так называемые катодные лучи, изучая которые Дж.Томсон впервые измерил заряд и массу электрона.

Зако́н сохране́ния электри́ческого заря́да гласит, что алгебраическая сумма зарядов электрически замкнутой системы сохраняется.

Закон сохранения заряда выполняется абсолютно точно. На данный момент его происхождение объясняют следствием принципа калибровочной инвариантности^[1][2]. Требование релятивистской инвариантности приводит к тому, что закон сохранения заряда имеет локальный характер: изменение заряда в любом наперёд заданном объёме равно потоку заряда через его границу. В изначальной формулировке был бы возможен следующий процесс: заряд исчезает в одной точке пространства и мгновенно возникает в другой. Однако такой процесс был бы релятивистски неинвариантен: из-за относительности одновременности в некоторых системах отсчёта заряд появился бы в новом месте до того, как исчез в предыдущем, а в некоторых — заряд появился бы в новом месте спустя некоторое время после исчезновения в предыдущем. То есть был бы отрезок времени, в течение которого заряд не сохраняется. Требование локальности позволяет записать закон сохранения заряда в дифференциальной и интегральной форме.

2. Зако́н Куло́на — это закон, описывающий силы взаимодействия между точечными электрическими зарядами.

Был открыт Шарлем Кулоном в 1785 г. Проведя большое количество опытов с металлическими шариками, Шарль Кулон дал такую формулировку закона:

Модуль силы взаимодействия двух точечных зарядов в вакууме прямо пропорционален произведению модулей этих зарядов и обратно пропорционален квадрату расстояния между ними

Иначе: Два точечных заряда в вакууме действуют друг на друга с силами, которые пропорциональны произведению модулей этих зарядов, обратно пропорциональны квадрату расстояния между ними и направлены вдоль прямой, соединяющей эти заряды. Эти силы называются электростатическими (кулоновскими).

Важно отметить, что для того, чтобы закон был верен, необходимы:

1. точечность зарядов — то есть расстояние между заряженными телами много больше их размеров — впрочем, можно доказать, что сила взаимодействия двух объёмно распределённых зарядов со сферически симметричными непересекающимися пространственными распределениями равна силе взаимодействия двух эквивалентных точечных зарядов, размещённых в центрах сферической симметрии;

2. их неподвижность. Иначе вступают в силу дополнительные эффекты: магнитное поле движущегося заряда и соответствующая ему дополнительная сила Лоренца, действующая на другой движущийся заряд;

3. взаимодействие в вакууме.

Однако с некоторыми корректировками закон справедлив также для взаимодействий зарядов в среде и для движущихся зарядов.^[1]

В векторном виде в формулировке Ш. Кулона закон записывается следующим образом:

где   — сила, с которой заряд 1 действует на заряд 2;   — величина зарядов;   — радиус-вектор (вектор, направленный от заряда 1 к заряду 2, и равный, по модулю, расстоянию между зарядами —  );   — коэффициент пропорциональности. Таким образом, закон указывает, что одноимённые заряды отталкиваются (а разноимённые — притягиваются).

Принцип суперпозиции.

Если заряженное тело взаимодействует одновременно с несколькими заряженными телами, то результирующая сила, действующая на данное тело, равна векторной сумме сил, действующих на это тело со стороны всех других заряженных тел.

3.

Напряженность электрического поля. Количественной характеристикой силового действия электрического поля на заряженные тела служит векторная величина E, называемая напряжённостью электрического поля.

E = F / q _пр.

Она определяется отношением силы F, действующей со стороны поля на точечный пробный заряд q_пр, помещенный в рассматриваемую точку поля, к величине этого заряда.

Понятие «пробный заряд» предполагает, что этот заряд не участвует в создании электрического поля и так мал, что не искажает его, т. е. не вызывает перераспределения в пространстве зарядов, создающих рассматриваемое поле. В системе СИ единицей напряженности служит 1 В / м, что эквивалентно 1 Н / Кл.

Линией напряженности электрического поля называется линия, касательная к которой в каждой точке совпадает с вектором напряженности 

Линии напряженности электростатического поля начинаются на положительных электрических зарядах и кончаются на отрицательных электрических зарядах или уходят в бесконечность.

Распределение линий напряженности вокруг точечного заряда показано на рис. 106 а, б.

Определяя направление вектора   в различных точках пространства, можно представить картину распределения линий напряженности электрического поля.

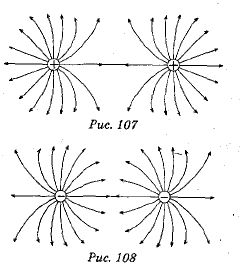
Для двух одноименных зарядов эта картина имеет вид, показанный на рис. 107, для разноименных — на рис. 108.

Принцип суперпозиции.

Если заряженное тело взаимодействует одновременно с несколькими заряженными телами, то результирующая сила, действующая на данное тело, равна векторной сумме сил, действующих на это тело со стороны всех других заряженных тел.

4.

Примеры решения задач

Найти напряженность электрического поля, создаваемого равномерно заряженным тонким стержнем 5длиной 2a на рас-стоянии R от его середины. Плотность заряда на стержне  > 0.

Решение.

В этом примере воспользуемся принципом суперпозиции электрических полей и разобьём стержень на малые элементы dx (dx << R). Из точки А они представляются точечными зарядами величиной dq = dx.

Н апряженность электрического поля, создаваемого в точке А только этим элементом стержня определяется соотношением

.

При интегрировании вдоль стержня (L) для определения результирующей напряженности Е, очевидно, будут складываться векторы dE различного направления. Разобьем эти векторы на две компоненты dE и dE, тогда

.

В силу симметрии задачи сумма векторов dE от всех участков стержня равна нулю, и задача существенно упрощается:

.

Так как теперь складываются только сонаправленные векторы dE, то можно перейти к суммированию их модулей:

. (*)

Для интегрирования удобно перейти к одной переменной –углу . Выразим для этого координату элемента стержня:

x = Rtg.

Отсюда:  .

Подставляя в (*)  , получаем:

,

где  , отсюда окончательно:

.

Если стержень очень длинный (“бесконечный”,  ), то:

. (6.7)

 

При изучении механики материальной точки, в особенности её разделов, связанных с движением по криволинейной траектории, часто оказываются полезными астрономические приложения. В условиях поверхности Земли набор естественных траекторий практически сводится к параболе. В космосе, наоборот, представлены многие типы криволинейного движения: вращение по окружности, а также эллиптические, параболические и гиперболические траектории разной степени вытянутости 

Задача

Определить напряженность электрического поля E(x) на оси равномерно заряженного кольца радиуса R. Заряд кольца q, x – расстояние от центра кольца.

Р ешение:

При решении задачи воспользуемся принципом суперпозиции. Для этого разобьём кольцо на элементы – точечные заряды q, каждый из которых создает в точке А напряженность

.

В следствие симметрии задачи вклад в общую напряженность дадут лишь вертикальные составляющие Е (сравните со случаем задачи 6.1). Поэтому напряженность в точке А будет определятся только суммой Е по всем элементам кольца:

Зависимость проекции Ex на ось Х вектора напряжённости представлена на графике. Видно, что на малых расстояниях от центра кольца эта зависимость линейная, на больших – обратно пропорциональна квадрату расстояния (кольцо “становится” точечным зарядом). Направлен вектор E вдоль оси Х.

Задача

Определить напряженность электрического поля Е на оси тонкого равномерно заряженного диска радиуса R. Поверхностная плотность заряда диска равна .

Р ешение:

При решении этой задачи воспользуемся также принципом суперпозиции. Для этого диск разбивается на кольца радиуса r и шириной dr. Тогда для напряженности поля такого кольца dE(x) можно записать (см. задачу 6.3):

, 

где dq =dS = 2rdr. Выражение для напряженности поля диска получается интегрированием dE по всем значениям r от 0 до R:

.

Нетрудно видеть, что при R   получается выражение для напряженности поля бесконечной плоскости: Е = /20.

Задача

Определить напряженность поля E(r) внутри шара радиуса R, объемная плотность заряда которого (r)=r1/2, где  – коэффициент пропорциональности, r – расстояние от центра шара, диэлектрическая проницаемость материала шара .

Решение:

Исходя из радиальной симметрии электрического поля, выберем замкнутую поверхность  – сферу с центром, совпадающим с центром шара и с радиусом r < R. В силу радиальной симметрии электрического поля легко рассчитать:

.

Сумма зарядов, оказавшихся внутри поверхности  равна:

,

Согласно теореме Гаусса, можно записать:

 откуда 

 

Теорема Гаусса для диэлектриков. Поток вектора электрического смещения. Связь поляризованности с плотностью связанных зарядов. Поле на границе раздела ди­электриков. Уравнение электромагнитной волны в диэлектрике. Оптические константы Среды. Нормальное падение волны на поверхность раздела двух диэлектриков и поверхность металла. 

5.

В пдф есть el_m1-7.pdf

6.

Электрическое поле наглядно изображается с помощью силовых линий. Силовой линией электрического поля называется линия, в каждой точке которой касательная совпадает с вектором напряженности поля. Силовые линии проводятся с такой густотой, чтобы число линий, пронизывающих воображаемую площадку 1м², перпендикулярную полю, равнялось величине напряженности поля в данном месте. Тогда по изображению электрического поля можно судить не только о направлении, но и о величине напряженности поля. Электрическое поле называется однородным, если во всех его точках напряженность Е одинакова. В противном случае поле называется неоднородным.

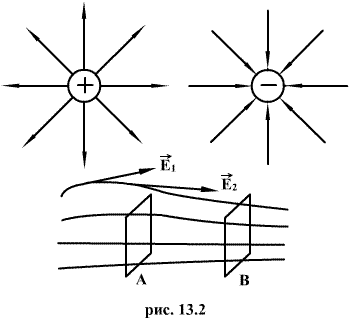
При положительном заряде, образующем поле, вектор напряженности направлен вдоль радиуса от заряда, при отрицательном - вдоль радиуса по направлению к заряду. Исходя из положительного заряда (или входя в отрицательный заряд) силовые линии теоретически простираются до бесконечности.

Итак, на примерах мы показали, что, если силовые линии однородного электрического поля напряженностью   пронизывают некоторую площадку S, то поток вектора напряженности (раньше мы называли число силовых линий через площадку) будет определяться формулой:

где E_n – произведение вектора   на нормаль   к данной площадке (рис. 2.5).

  Рис. 2.5

       Полное число силовых линий, проходящих через поверхность S называется потоком вектора напряженности Ф_Е через эту поверхность.

       В векторной форме можно записать   – скалярное произведение двух векторов, где вектор  .

       Таким образом, поток вектора   есть скаляр, который в зависимости от величины угла α может быть как положительным, так и отрицательным.

7.

Поток вектора напряженности через произвольную замкнутую поверхность равен алгебраической сумме зарядов, расположенный внутри этой поверхности деленной на электрическую постоянную.

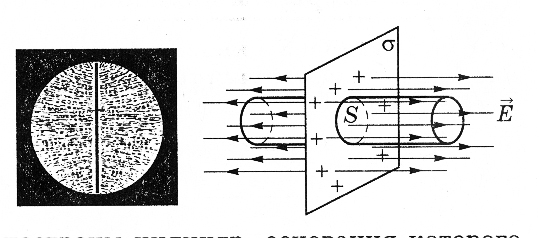
Напряженность поля заряженной плоскости

(1)

(2)

Бесконечная плоскость, заряженная с поверхностной плотностью заряда : для расчета напряженности электрического поля, созданного бесконечной плоскостью, выделим в пространстве цилиндр, ось которого перпендикулярна заряженной плоскости, а основания – параллельны ей и одно из оснований проходит через интересующую нас точку поля. Согласно теореме Гаусса поток вектора напряженности электрического поля сквозь замкнутую поверхность равен:

Ф= , с другой стороны он же: Ф=E

Приравняем правые части уравнений:

= E

Выразим = - через поверхностную плотность заряда и найдем напряженность электрического поля:

Найдем напряженность электрического поля между разноименно заряженными пластинами с одинаковой поверхностной плотностью:

(1)

(2)

(3)

Найдем поле вне пластин:

; ; (4)

Напряженность поля заряженной сферы

(1)

Ф= (2) т. Гаусса

Ф=ES (3)

для r < R

; , т.к. (внутри сферы нет зарядов)

Для r = R

( ; ; )

Для r > R

Напряженность поля, созданного шаром, заряженным равномерно по всему объему

Объемная плотность заряда,

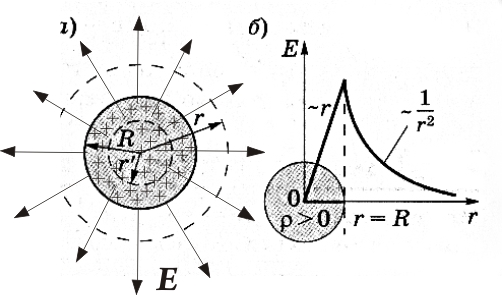распределенного по шару:

(1)

(2)

Для r < R

( ; Ф= )

Для r = R

Для r > R

8.

РАБОТА ЭЛЕКТРОСТАТИЧЕСКОГО ПОЛЯ ПО ПЕРЕМЕЩЕНИЮ ЗАРЯДА

Электростатическое поле - эл. поле неподвижного заряда. Fэл , действующая на заряд, перемещает его, совершая раборту. В однородном электрическом поле Fэл = qE - постоянная величина

Работа поля (эл. силы) не зависит от формы траектории и на замкнутой траектории = нулю.

Циркуляция вектора напряженности электростатического поля

В случае, если в электростатическом поле точечного заряда Q из точки 1 в точку 2 вдоль какой-либо траектории (рис. 1) двигается другой точечный заряд Q0, то сила, которая приложена к заряду, совершает некоторую работу. Работа силы F на элементарном перемещении dl равна    Так как dl/cosα=dr, то    Работа при перемещении заряда Q0 из точки 1 в точку 2   (1)  от траектории перемещения не зависит, а определяется только положениями начальной 1 и конечной 2 точек. Значит, электростатическое поле точечного заряда является потенциальным, а электростатические силы — консервативными  Из формулы (1) видно, что работа, которая совершается при перемещении электрического заряда во внешнем электростатическом поле по произвольному замкнутому пути L, равна нулю, т.е.   (2)  Если в качестве заряда, которого перемещают в электростатическом поле, взять единичный точечный положительный заряд, то элементарная работа сил поля на пути dl равна Еdl = Eldl, где El = Ecosα — проекция вектора Е на направление элементарного переме¬щения. Тогда формулу (2) можно представить в виде   (3)  Интеграл   называется циркуляцией вектора напряженности. Значит, циркуляция вектора напряженности электростатического поля вдоль любого замкнутого контура равна нулю. Силовое поле, которое обладает свойством (3), называетсяпотенциальным. Из равенства нулю циркуляции вектора Е следует, что линии напряженности электростатического поля не могут быть замкнутыми, они обязательно начинаются и кончаются на зарядах (на положительных или отрицательных) или же идут в бесконечность.  Формула (3) верна только для электростатического поля. В дальнейшем будет показано, что с случае поля движущихся зарядов условие (3) не верно (для него циркуляция вектора напряженности отлична от нуля).

Теорема о циркуляции для электростатического поля.

Поскольку электростатическое поле является центральным, то силы, действующие на заряд в таком поле, являются консервативными. Так как   представляет собой элементарную работу, которую силы поля производят над единичным зарядом, то работа консервативных сил на замкнутом контуре равна

9.

Потенциал

Система "заряд - электростатическое поле" или "заряд - заряд" обладает потенциальной энергией, подобно тому, как система "гравитационное поле - тело" обладает потенциальной энергией.

Физическая скалярная величина, характеризующая энергетическое состояние поля называетсяпотенциалом данной точки поля. В поле помещается заряд q, он обладает потенциальной энергией W. Потенциал - это характеристика электростатического поля.

Вспомним потенциальную энергию в механике. Потенциальная энергия равна нулю, когда тело находится на земле. А когда тело поднимают на некоторую высоту, то говорят, что тело обладает потенциальной энергией.

Касательно потенциальной энергии в электричестве, то здесь нет нулевого уровня потенциальной энергии. Его выбирают произвольно. Поэтому потенциал является относительной физической величиной.

Потенциальная энергия поля - это работа, которую выполняет электростатическая сила при перемещении заряда из данной точки поля в точку с нулевым потенциалом.

Рассмотрим частный случай, когда электростатическое поле создается электрическим зарядом Q. Для исследования потенциала такого поля нет необходимости в него вносить заряд q. Можно высчитать потенциал любой точки такого поля, находящейся на расстоянии r от заряда Q.

Диэлектрическая проницаемость среды имеет известное значение (табличное), характеризует среду, в которой существует поле. Для воздуха она равна единице.

Разность потенциалов

Работа поля по перемещению заряда из одной точки в другую, называется разностью потенциалов

Эту формулу можно представить в ином виде

Принцип суперпозиции

Потенциал поля, созданного несколькими зарядами, равен алгебраической (с учетом знака потенциала) сумме потенциалов полей каждого поля в отдельности

Энергия электростатического поля - это энергия системы неподвижных точечных зарядов, энергия уединенного заряженного проводника и энергия заряженного конденсатора.

Если имеется система двух заряженных проводников (конденсатор), то полная энергия системы равна сумме собственных потенциальных энергий проводников и энергии их взаимодействия:

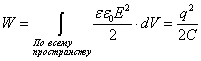
Энергия электростатического поля системы точечных зарядов равна: 

10.

Равномерно заряженная плоскость. Напряжённость электрического поля, создаваемого бесконечной плоскостью, заряженной с поверхностной плотностью заряда  , можно рассчитать, воспользовавшись теоремой Гаусса. 

Из условий симметрии следует, что вектор E везде перпендикулярен плоскости. Кроме того, в симметричных относительно плоскости точках вектор E будет одинаков по величине и противоположен по направлению.  В качестве замкнутой поверхности выберем цилиндр, ось которого перпендикулярна плоскости, а основания расположены симметрично относительно плоскости, как показано на рисунке.  Так как линии напряжённости параллельны образующим боковой поверхности цилиндра, то поток через боковую поверхность равен нулю. Поэтому поток вектораЕ через поверхность цилиндра

,

где   - площадь основания цилиндра. Цилиндр вырезает из плоскости заряд  . Если плоскость находится в однородной изотропной среде с относительной диэлектрической проницаемостью  , то

.

Когда напряженность поля не зависит от расстояния между плоскостями, такое поле называют однородным. График зависимости E (x) для плоскости.

Разность потенциалов между двумя точками, находящимися на расстояниях R₁ и R₂от заряженной плоскости, равна 

Пример 2. Две равномерно заряженные плоскости.  Рассчитаем напряжённость электрического поля, создаваемого двумя бесконечными плоскостями. Электрический заряд распределен равномерно с поверхностной плотностями   и  . Напряженность поля найдем как суперпозицию напряжённостей полей каждой из плоскостей. Электрическое поле отлично от нуля только в пространстве между плоскостями и равно  . 

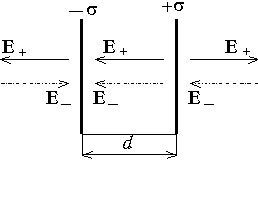
Разность потенциалов между плоскостями  , где d - расстояние между плоскостями.  Полученные результаты могут быть использованы для приближённого расчета полей, создаваемых плоскими пластинами конечных размеров, если расстояния между ними много меньше их линейных размеров. Заметные погрешности таких расчётов появляются при рассмотрении полей вблизи краев пластин. График зависимости E (x) для двух плоскостей. 

Пример 3. Тонкий заряженный стержень.  Для расчёта напряжённости электрического поля, создаваемого очень длинным  заряженным с линейной плотностью заряда   стержнем, используем теорему Гаусса. На достаточно больших расстояниях от концов стержня линии напряжённости электрического поля направлены радиально от оси стержня и лежат в плоскостях, перпендикулярных этой оси. Во всех точках, равноудалённых от оси стержня, численные значения напряжённости одинаковы, если стержень находится в однородной изотропной среде с относительной диэлектрической проницаемостью  . 

Для расчета напряженности поля в произвольной точке, находящейся на расстоянииr от оси стержня, проведём через эту точку цилиндрическую поверхность  (см. рисунок). Радиус этого цилиндра равен r, а его высота h.  Потоки вектора напряжённости через верхнее и нижнее основания цилиндра будут равны нулю, так как силовые линии не имеют составляющих, нормальных к поверхностям этих оснований. Во всех точках боковой поверхности цилиндра Е = const.  Следовательно, полный поток вектора E через поверхность цилиндра будет равен 

 ,

По теореме Гаусса, поток вектора E равен алгебраической сумме электрических зарядов, находящихся внутри поверхности (в данном случае цилиндра) делённой на произведение электрической постоянной   и относительной диэлектрической проницаемости среды 

,

где   заряд той части стержня, которая находится внутри цилиндра. Следовательно, напряжённость электрического поля 

.

Разность потенциалов электрического поля между двумя точками, находящимися на расстояниях R₁ и R₂ от оси стержня, найдём, пользуясь связью между напряжённостью и потенциалом электрического поля. Так как напряжённость поля изменяется только в радиальном направлении, то 

Пример 4. Заряженная сферическая поверхность.  Электрическое поле, создаваемое сферической поверхностью, по которой равномерно распределён электрический заряд с поверхностной плотностью  , имеет центрально-симметричный характер. 

Линии напряжённости направлены по радиусам от центра сферы, а модуль вектораE зависит только от расстояния r от центра сферы. Для расчёта поля выберем замкнутую сферическую поверхность радиуса r.  При r^o<R^o (внутри сферы) Е = 0.  Напряжённость поля равна нулю, так как внутри сферы заряд отсутствует.  При r > R (вне сферы), согласно теореме Гаусса

 ,

где   - относительная диэлектрическая проницаемость среды, окружающей сферу.

.

Напряжённость уменьшается по тому же закону, что и напряженность поля точечного заряда, т. е. по закону  .  При r^o<R^o (внутри сферы)  . При r > R (вне сферы)  .  График зависимости E (r) для сферы. 

Пример 5. Заряженный по объему шар из диэлектрика.  Если шар радиусом R из однородного изотропного диэлектрика с относительной проницаемостью   равномерно заряжен по объёму с плотностью  , то создаваемое им электрическое поле также является центрально-симметричным.  Как и в предыдущем случае, выберем замкнутую поверхность для расчёта потока вектора E в виде концентрической сферы, радиус которой r может изменяться от 0 до  .  При r < R поток вектора E через эту поверхность будет определяться зарядом

, так что

При r < R (внутри шара)  . Внутри шара напряжённость возрастает прямо пропорционально расстоянию от центра шара. Вне шара (при r > R) в среде с диэлектрической проницаемостью  , поток вектора E через поверхность будет определяться зарядом  .  При r^o>R^o (вне шара)  .  На границе "шар - окружающая среда" напряжённость электрического поля изменяется скачком, величина которого зависит от соотношения диэлектрических проницаемостей шара и среды. График зависимости E (r) для шара ( ). 

Вне шара (r > R) потенциал электрического поля меняется по закону 

 .

Внутри шара (r < R) потенциал описывается выражением 

.

В заключение, приведем выражения для расчета напряженностей полей заряженных тел, различной формы

11.

Разность потенциалов
Напряжение — разность значений потенциала в начальной и конечнойточках траектории.  Напряжение численно равно работе электростатического поля при перемещении единичного положительного заряда вдоль силовых линий этого поля.          Разность потенциалов (напряжение) не зависит от выбора системы координат!
Единица разности потенциалов      Напряжение равно 1 В, если при перемещении положительного заряда в 1 Кл вдоль силовых линий поле совершает работу в 1 Дж.

12.

Проводник – это твердое тело, в котором имеются “свободные электроны”, перемещающиеся в пределах тела.

Металлические проводники в целом являются нейтральными: в них поровну отрицательных и положительных зарядов. Положительно заряженные – это ионы в узлах кристаллической решетки, отрицательные – электроны, свободно перемещающиеся по проводнику. Когда проводнику сообщают избыточное количество электронов, он заряжается отрицательно, если же у проводника «отбирают» какое-то количество электронов, он заряжается положительно.

Избыточный заряд распределяется только по внешней поверхности проводника.

1.6.1. Условия равновесия зарядов на проводнике

1. Напряженность поля  в любой точке внутри проводника равна нулю.

2. Вектор   на поверхности проводника   направлен по нормали к каждой точке поверхности проводника.

Действительно, если бы  условие 1 не выполнялось, то подвижные носители электрических зарядов, имеющиеся в каждом проводнике, под действием сил поля пришли бы в движение (в проводнике возник бы электрический ток) и равновесие было бы нарушено. 

Из 1 следует, что поскольку

Из того факта, что поверхность проводника эквипотенциальна следует, что непосредственно у этой поверхности поле  направлено по нормали к ней в каждой точке (условие 2). Если бы это было не так, то под действием касательной составляющей   заряды пришли бы в движение по поверхности проводника. т.е. равновесие зарядов на проводнике было бы невозможным.

Из 1 следует, что поскольку

Внутри  проводника избыточных зарядов нет.

Заряды распределяются только на поверхности проводника с некоторой плотностью   и находятся в очень тонком поверхностном слое (его толщина около одного-двух межатомных расстояний).

13.

Плотность заряда — это количество заряда, приходящееся на единицу длины, площади или объёма, таким образом определяются линейная, поверхностная и объемная плотности заряда, которые измеряются в системе СИ: в Кулонах на метр [Кл/м], в Кулонах на квадратный метр [Кл/м²] и в Кулонах на кубический метр [Кл/м³], соответственно. В отличие от плотности вещества, плотность заряда может иметь как положительные, так и отрицательные значения, это связано с тем, что существуют положительные и отрицательные заряды.

14.

Общая задача электростатики

Вектор напряженности  ,

по теореме Гаусса   

 - уравнение Пуассона.

В случае   - нет зарядов между проводниками, получаем

 - уравнение Лапласа.

Пусть известны граничные условия на поверхностях проводников: значения  ; тогда данная задача имеет единственное решение согласно теореме единственности.

При решении задачи определяется значение   и затем поле   между проводниками   определяется распределение зарядов на проводниках (по вектору напряженности у поверхности).

Рассмотрим пример. Найдем напряженность в пустой полости проводника.

Потенциал в полости удовлетворяет уравнению Лапласа;

потенциал на стенках проводника  .

Решение уравнения Лапласа в этом случае тривиальное, и по теореме единственности других решений нет 

, т.е. поля в полости проводника нет.

Уравне́ние Пуассо́на — эллиптическое дифференциальное уравнение в частных производных, которое, среди прочего, описывает

• электростатическое поле,

• стационарное поле температуры,

• поле давления,

• поле потенциала скорости в гидродинамике.

Оно названо в честь знаменитого французского физика и математика Симеона Дени Пуассона.

Это уравнение имеет вид: 

где   — оператор Лапласа или лапласиан, а   — вещественная или комплексная функция на некотором многообразии.

В трёхмерной декартовой системе координат уравнение принимает форму:

В декартовой системе координат оператор Лапласа записывается в форме   и уравнение Пуассона принимает вид:

Если f стремится к нулю, то уравнение Пуассона превращается в уравнение Лапласа (уравнение Лапласа — частный случай уравнения Пуассона):

Уравнение Пуассона может быть решено с использованием функции Грина; см., например, статью экранированное уравнение Пуассона. Есть различные методы для получения численных решений. Например, используется итерационный алгоритм — «релаксационный метод».

15.

Электрическая емкость уединенного проводника

Будем рассматривать уединенный проводник, т. е. проводник, значительно удаленный от других проводников, тел и зарядов. Его потенциал, как известно, прямо пропорционален заряду проводника. Из опыта известно, что разные проводники, будучи при этом одинаково заряженными, имеют различные потенциалы. Поэтому для уединенного проводника можно записать    Величину   (1)  называют электроемкостью (или просто емкостью) уединенного проводника. Емкость уединенного проводника задается зарядом, сообщение которого проводнику изменяет его потенциал на единицу.  Емкость уединенного проводника зависит от его размеров и формы, но не зависит от материала, формы и размеров полостей внутри проводника, а также его агрегатного состояния. Причиной этому есть то, что избыточные заряды распределяются на внешней поверхности проводника. Емкость также не зависит ни от заряда проводника, ни от его потенциала.  Единица электроемкости — фарад (Ф): 1 Ф — емкость такого уединенного проводника, у которого потенциал изменяется на 1 В при сообщении ему заряда 1 Кл.  Согласно формуле потенциала точечного заряда, потенциал уединенного шара радиуса R, который находится в однородной среде с диэлектрической проницаемостью ε, равен    Применяя формулу (1), получим, что емкость шара   (2)  Из этого следует, что емкостью 1 Ф обладал бы уединенный шар, находящийся в вакууме и имеющий радиус R=C/(4πε0)≈9•106 км, что примерно в 1400 раз больше радиуса Земли (электроемкость Земли С≈0,7 мФ). Следовательно, фарад — довольно большая величина, поэтому на практике применяются дольные единицы - миллифарад (мФ), микрофарад (мкФ), нанофарад (нФ), пикофарад (пФ). Из формулы (2) следует также, что единица электрической постоянной ε0 — фарад на метр (Ф/м) (см. (78.3)).

16.

Конденса́тор (от лат. condensare — «уплотнять», «сгущать») — двухполюсник с определённым значением ёмкости и малой омической проводимостью; устройство для накоплениязаряда и энергии электрического поля. Конденсатор является пассивным электронным компонентом. Обычно состоит из двух электродов в форме пластин (называемых обкладками), разделённых диэлектриком, толщина которого мала по сравнению с размерами обкладок.