Задание 1. По имеющимся данным требуется;

1. Построить статистический ряд распределения, изобразить получившийся ряд графически с помощью полигона или гистограммы. Найти функцию распределения, построить ее график.

2. Найти: выборочную среднюю, выборочную дисперсию, среднее квадратическое отклонение выборки, моду и медиану.

3. Проверитъ при уровне значимости α = 0,05 гипотезу о соответствии

имеющегося статистического распределения нормальному закону.

4. Считая данные нормально распределенной случайной величиной найти:

а) точечную оценку математического ожидания изучаемой совокупности;

б) доверительный интервал для математического ожидания с доверительной

вероятностью 0,95.

1. Для удобства проранжируем полученные данные и составим вариационный ряд, т.е. расположим их в порядке возрастания:

36, 45, 46, 46, 48, 51, 52, 57, 58, 60, 62, 63, 67, 69, 70, 73, 73, 74, 75, 76, 77, 78, 79, 79, 80, 81, 82, 82, 82, 83, 84, 85, 86, 87, 88, 89, 90, 91, 94, 99, 102, 105, 108, 111, 118.

Так как число значений случайной величины Х – «численность работающих в от-расли человек» – достаточно велико, то построим интервальный статистический ряд.

Определим: х_min = 36, x_max = 118; объем выборки n = 45.

По формуле Стерджесса при n = 45 находим длину частичного интервала:

Принимаем h = 12. Тогда .

Число интервалов m = 1 + 3,32lgn = 1 + 3,32lg45 = 6,4 ≈ 6.

Исходные данные разбиваем на 6 интервалов: [30, 42), [42, 54), [54, 66), [66, 78),

[78, 90), [90, 102), [102, 118)

Подсчитав численность работающих в отрасли (частоту n_i), попавших в каждый из полученных интервалов, и вычислив для каждого интервала частость построим интервальный статистический ряд (таблица 1):

Таблица 1

xi – xi+1	30 – 42	42 – 54	54 – 66	66 – 78	78 – 90	90 – 102	102 – 118
Частота ni	1	6	5	9	15	4	5
Частость	0,02	0,13	0,11	0,21	0,33	0,09	0,11

Построим гистограмму, отложив по оси абсцисс интервалы, а по оси ординат – частости.

По полученным результатам находим функцию распределения F*(x).

Очевидно, что для имеем F*(x) = 0, так как n_i = 0. Подсчитаем значения функции F*(x) в виде «наращенной относительной частоты» и составим таблицу 2.

Таблица 2

Интервал	(-∞, 30)	[30, 42)	[42, 54)	[54, 66)	[66, 78)	[78, 90)	[90, 102)	[102, 118)
F*(x)	0	0,02	0,15	0,26	0,47	0,80	0,89	1,000

По полученным результатам строим график функции распределения

2. Для нахождения числовых характеристик выборки в качестве представителей каждого интервала возьмем их середины (таблица 3).

Таблица 3

Интервал	30 – 42	42 – 54	54 – 66	66 – 78	78 – 90	90 – 102	102 – 118
Середина интервала xi	36	48	60	72	84	96	110
Частота ni	1	6	5	9	15	4	5
Частость	0,02	0,13	0,11	0,21	0,33	0,09	0,11
Накопленная частота	1	7	12	21	36	40	45

Выборочная средняя определяется как среднее арифметическое полученных при выборки значений:

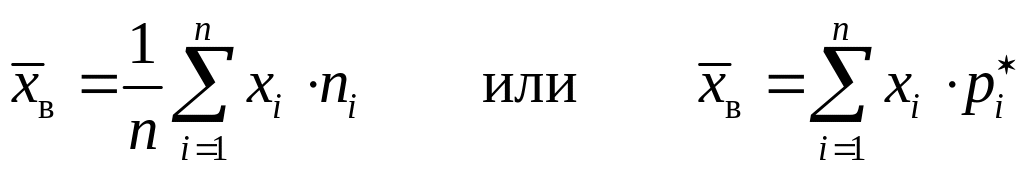
= 36·0,02 + 48·0,13 + 60·0,11 + 72·0,21 + 84·0,33 + 96·0,09 + 110·0,11 = 77

Выборочная дисперсия вычисляется по одной из формул:

D_в = (36–77)²·0,02 + (48–77)²·0,13 + (60–77)²·0,11 + (72–77)²·0,21 + (84–77)²·0,33 +

+ (96–77)²·0,09 + (110–77)²·0,11 = 348

Выборочное среднее квадратическое отклонение равно:

Мода М₀ – варианта, имеющая наибольшую частоту, для интервального статис-тического ряда вычисляется по формуле:

где - начало модального интервала; - частота модального интервала; - частота интервала, предшествующего модальному; - частота интервала, следующего за модальным.

Тогда:

Медиана М_е – значение признака (варианта), приходящееся на середину вариаци-онного ряда, для интервального статистического ряда вычисляется по формуле:

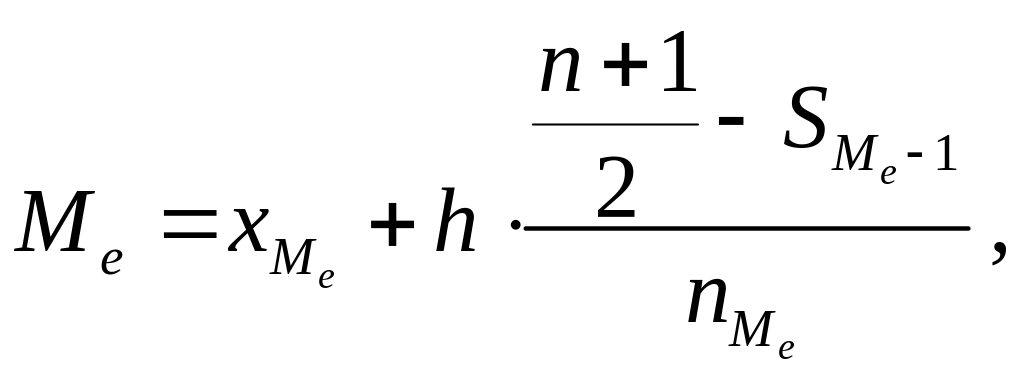
где - начало медианного интервала; - частота медианного интервала; - накопленная частота интервала, предшествующего медианного.

Медианным интервалом является интервал (78 – 90), для него S_n = 36 > n/2 = 22,5, а для предшествующего интервала (66 – 78) S_n = 21 < n/2. Тогда:

3. Число значений (частота) случайной величины Х в крайних интервалах меньше 5, поэтому объединяем их с соседними (таблица 4).

Таблица 4

Интервал	30 – 54	54 – 66	66 – 78	78 – 90	90 – 118
Середина интервала xi	42	60	72	84	104
Частота ni	7	5	9	15	9
Частость	0,15	0,11	0,21	0,33	0,2

Вычислим выборочные среднюю, дисперсию и среднее квадратическое отклонение:

= 42·0,15 + 60·0,11 + 72·0,21 + 84·0,33 + 104·0,2 =76,5

D_в = (42–76,5)²·0,15 + (60–76,5)²·0,11 + (72–76,5)²·0,21 + (84–76,5)²·0,33 +

+ (104–76,5)²·0,2 = 382,6

Находим вероятности р_i (i = 1;5). При распределении случайной величины Х по нормальному закону с параметрами (а, σ) на интервале (-∞, +∞), то крайние интервалы в ряде распределения заменяем соответственно на (-∞, 54) и (90, +∞).

Тогда вероятность попадания Х в интервал вычисляется по формуле:

где Ф(х) – функция Лапласа.

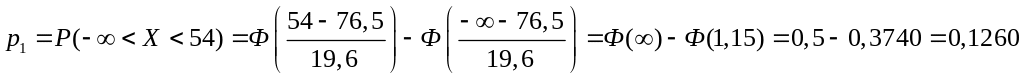
Контроль: 0,1260+0,1686+0,2373+0,2230 +0,2451 = 1

Полученные результаты сводим в таблицу 5

Таблица 5

xi – xi+1	-∞ – 54	54 – 66	66 – 78	78 – 90	90 – +∞
ni	7	5	9	15	9
	5,67	7,59	10,68	10,03	11,03

Вычисляем :

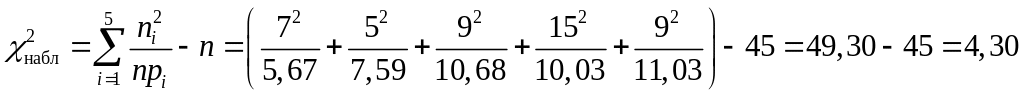
т.е.

Находим число степеней свободы: по выборке рассчитаны два параметра, значит, r = 2. Количество интервалов m = 5. Следовательно, k = 5 – 2 – 1 =2. При α = 0,05 и k = 2 по таблице распределения находим . Так как , то нет оснований отвергнуть проверяемую гипотезу.

4. а) По методу моментов при нормальном распределении случайной величины Х теоретический начальный момент I порядка приравниваем эмпирическому моменту I порядка: v₁ = М_э.

Так как v₁ равно математическому ожиданию (v₁ = М_х), а , то , т.е. точечной оценкой математического ожидания является средняя выборочная.

б) Доверительный интервал для математического ожидания нормально распреде-ленной случайной величины при неизвестной дисперсии определяется неравен-ством:

где S – исправленное среднее квадратическое отклонение случайной величины Х, вычисленное по выборке: ; t_γ – коэффициент, опреде-ляемый по таблице квантилей распределения Стьюдента в зависимости от дове-рительной вероятности γ и числа степеней свободы n–1.

По данным таблицы 3 имеем: = 77, находим S:

По таблице значений t_γ для γ = 0,95 и n–1=44 имеем t_γ = 2,016. Тогда:

Задание 2. По приведенным ниже данным требуется: