Решаем это уравнение относительно :

Полученный результат округляем в сторону увеличения припуска Z₁₁ и окончательно получаем: A₅ = 150,2_–0,25.

Решаем размерную цепь № 8.

						Известно: ; Найти: А2 + ТА2.

Основное уравнение размерной цепи имеет вид:

Z₈ = А₆ + А₈ + А₂ – А₇ .

Размерная цепь сложная, поэтому табличный припуск требует коррекции. Расчетный припуск определяем по выражению:

.

Здесь определяем следующим образом:

,

отсюда

, так как i = 8, i – 1 = 2,

где – припуск на чистовую подрезку после черновой обработки; ТА₂ = 0,15 – черновая обработка от обработанной базы. Тогда

;

Из основного уравнения размерной цепи следует:

.

Решаем это уравнение относительно :

.

Округляем и получаем:

.

Известно: . Найти: а4 – та4. Решаем размерную цепь № 6

					А4 – ТА4
					А6 – ТА6
	Z6

Данная цепь «простая». Записываем основное уравнение:

,

где – припуск на чистовую подрезку после черновой обработки.

– черновая обработка от обработанной базы.

Тогда . Окончательно .

Решаем размерную цепь № 5.

		Известно: . Найти: A3 – TA3 .

Данная цепь «простая». Записываем основное уравнение:

,

где Z₅ = 1,5 – припуск на чистовую подрезку после черновой обработки.

TA₃ = 0,4 – черновая обработка от обработанной базы. Тогда

.

В результате: .

Решаем размерную цепь № 4 .

Известно: 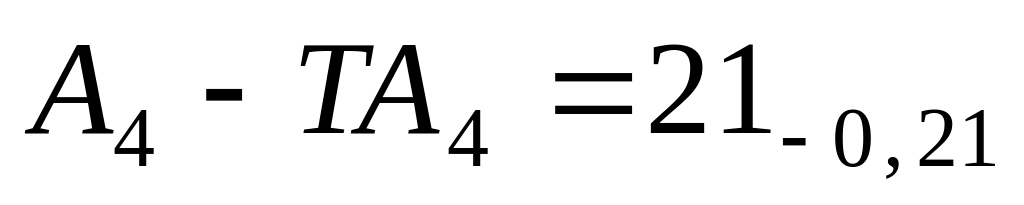. Найти: .

Данная цепь «простая». Записываем основное уравнение:

,

где Z₄ = 1,8 – припуск на черновую подрезку.

Этот припуск рассчитывается по методу Кована или берется из специальных таблиц. В ОСТ 1.41512–86 припуски на черновую обработку не приведены. В данных расчетах припуск на черновую подрезку получен увеличением припуска на чистовую подрезку в 1,5 раза; ТА₁ = 0,52 – черновая обработка от черновой базы.

Тогда .

В результате: .

Решаем размерную цепь № 1.

Известно: А1 – ТА1 = 22,8-0,52 . Найти: Н2 .			Н2
		А1 – ТА1
					Z1

Предельные отклонения на размер Н₂ известны:

.

Основное уравнение размерной цепи имеет вид:

.

Размерная цепь сложная, так как размер Н₂ имеет отклонение не «в тело». Поэтому

.

Здесь определяем следующим образом:

.

В этом выражении в качестве необходимо взять такое отклонение размера , которое делало бы рассматриваемую размерную цепь «простой». Поэтому в качестве берем . Тогда .

Отсюда , где – припуск на черновую подрезку. Тогда

;

Из основного уравнения следует: . Тогда . Окончательно .