15. Представление обратного расстояния с помощью шаровых гармоник.

Расстояние lмежду двумя точками со сферическими координатами

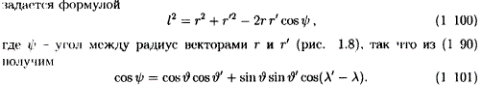
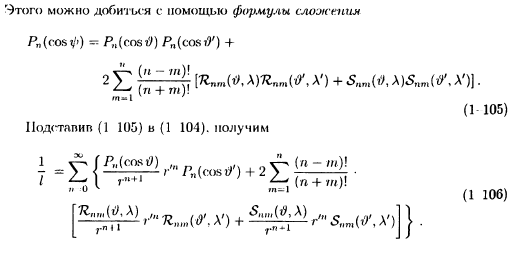
17. Теорема Стокса. Проблема Стокса.

Возможность принципиально строгого определения внешнего гравитационного, поля и фигуры Земли появилась после того, как было установлено, что внешний потенциал Земли (как любой планеты) может быть определен независимо от плотности.

Это положение было доказано в 1849 г. английским ученым

Стоксом. В основе теоретических исследований Стокса лежит

его теорема, которая может быть сформулирована следующим

образом: если известны общая масса М тела, угловая скорость

ω его вращения около неизменной оси и форма внешней

уровенной поверхности σ, целиком охватывающей все притягивающие массы, то потенциал силы тяжести W и сама сила тяжести g определяются однозначно как во всем внешнем пространстве, так и на самой уровенной поверхности.

Теорема Стокса может быть отнесена и к физической поверхности планеты, не являющейся уровенной; только в этом

случае необходимо знать на ее поверхности приращение потенциала силы тяжести относительно какого-либо начального

пункта.

Теорема Стокса не отвечает на вопрос: как может быть решена эта задача для данной конкретной уровенной поверхности. Нахождение потенциальной функции W составляет так называемую проблему Стокса. Поскольку потенциал Q центробежной силы выражается независимо от формы уровенной поверхности и распределения масс простой формулой , проблема Стокса сводится к нахождению потенциала притяжения V.

Решение проблемы Стокса для эллипсоида вращения позволяет

построить модель гравитационного поля Земли, весьма близко подходящую к ее действительному гравитационному полю. Можно подобрать эллипсоид, поверхность которого имеет минимальные отклонения от поверхности среднего уровня моря и гравитационное поле которого незначительно отличается от действительного поля Земли. Модель гравитационного поля принято называть нормальным гравитационным полем. Нормальное поле значительно проще действительного поля Земли; его уровенные поверхности и силовые линии могут быть использованы как координатные при определении положения точек физической поверхности Земли. Можно представить нормальное поле как поле идеального физического тела, заменяющего реальную Землю и называемого нормальной

Землей.

Построение нормального поля позволяет выделить из земного

гравитационного поля его основную часть и рассматривать

не полные элементы поля, а малые разности соответствующих элементов действительного и нормального полей. В этом случае

задача определения фигуры Земли будет заключаться в изучении

отступлений ее физической поверхности от поверхности «модели», а задача определения потенциала W сводится к определению небольших величин T=W—U, где U— потенциал силы тяжести эллипсоида, иначе называемый нормальным потенциалом З е м л и. Величина Тполучила название возмущающего потенциала Земли.

Рассмотрим кратко его свойства.

Представим нормальный потенциал Земли формулой, аналогичной W=V + Q для действительного потенциала,

Возмущающий потенциал обладает всеми свойствами потенциалов притяжения: потенциал Т, как и его первые производные, непрерывен, однозначен и конечен во всем пространстве, сумма его вторых производных во всем внешнем пространстве равна нулю (ΔT=0). На бесконечности потенциал Т является функцией регулярной. Возмущающий потенциал является характеристикой аномальности гравитационного поля Земли. Он определяет степень отступлений точек физической поверхности Земли от выбранной модели. Величины, характеризующие эти отступления, связаны с возмущающим потенциалом. Следовательно, определив возмущающий потенциал Земли, можно определить и ее фигуру.