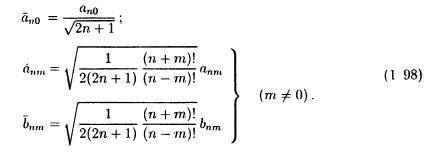13.Виды сферических функций и их основные свойства.

Чисто широтные изменения гравитационного поля Земли-

описываются членами, для которых индекс k=0, т. е. полиномами

Лежандра. Полиномы Лежандра Pno(cosθ) обращаются

в нуль на системе параллелей Земли, делящих ее поверхность

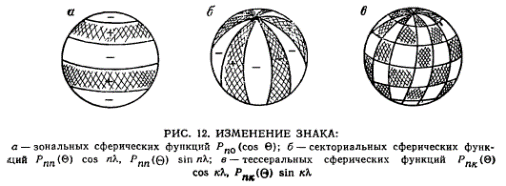
на (n+1) зоны, в которых функции Pn 0(cosθ) принимают положительные и отрицательные значения (рис. 12, а). По этой причине

полиномы Лежандра называются зональными сферическими

функциями.

Следует заметить, что каждая зональная гармоника симметрична

относительно полярной оси, причем четные гармоники

имеют симметрию также относительно экватора, тогда как нечетные

гармоники создают противоположный по знаку эффект

в южном и северном полушариях. При k=n сферические функции

обращаются в нуль на 2п меридианах,

принимая попеременно то положительные, то отрицательные

значения в сферических секторах, ограниченных этими

меридианами (рис. 12, б). Поэтому эти функции называются

с е к т о р и а л ь н ы м и . Наконец, при 0<k<n вся сфера сеткой

2k меридианов и п—k параллелей делится на сферические четырехугольники

(tessera), кроме полярных областей, где образуются

треугольники (рис. 12, в). Сферические функции

в каждых двух прилежащих четырехугольниках

принимают попеременно положительные и отрицательные

значения. Эти функции называются т е с с е р а л ь н ы м и.

14. Нормирование сферических функций и коэффициентов при сферических функциях.

Полностью нормированные сферические

функции

Формулы для разложения функции в ряд по сферическим

функциям не очень удобны в использовании. Взглянем на (1 84)

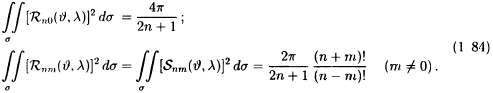
и

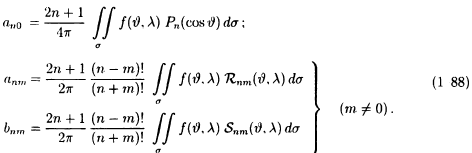
(1 88): они различны для m = 0 и m ≠ 0 и кроме того, довольно громоздки и

трудны для запоминания.

В связи с этим было предложено обычные сферические функции Rnm и

Snm, определяемые формулами (1 82)

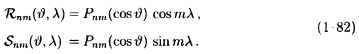
и (1 57)

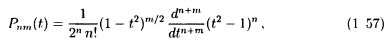
заменить другими, отличающимися

постоянным коэффициентом и более удобными в использовании. Вдальнейшем мы будем рассматривать только полностью нормированные сферические

функции, которые, по видимому, являются наиболее удобными и широко используемыми.

"Полностью нормированные” сферические функции являются просто "нормированными"

в смысле теории действительных функций; мы вынуждены использовать

эго громоздкое выражение, потому что термин "нормированные

сферические функции" уже был, к сожалению, применен к другим функциям.

часто не являющимся "нормированными" в математическом смысле.

Мы обозначим полностью нормированные сферические функции через , они определяются следующим образом:

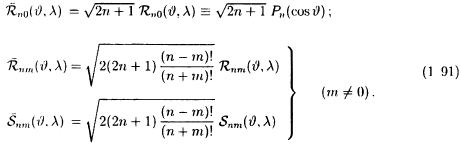
Свойство ортогональности (1 83) остается верным для полностью нормированных

функций, в то время, как формула (1 84) значительно упрощается

и выглядит так:

Эго значит, что средний квадрат любой полностью нормированной сферической

функции равен единице; среднее значение берется по поверхности сферы,

то есть интеграл делится на площадь сферы 4π. Эта формула теперь верна

для любого т, в том числе и для т = 0.

Если мы разложим произвольную функцию в ряд по полностью

нормированным сферическим функциям, аналогично (1 81),

то коэффициенты апmи Ьпт определяются просто:

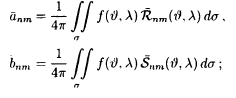(1 94)

то есть коэффициенты суть среднее по сфере значение произведения функции

на соответствующею сферическую функцию .

Простота формул (1 92) и (1 94) составляет главное преимущество полностью

нормированных сферических функций и делает их полезными во многих

отношениях, хотя функции в (1 91) более сложны, чем обычные

Rnm и Snm.Имеем

где

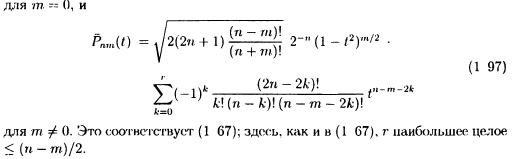
Ниже указаны соотношения между коэффициентами anm и Ьпт для полностью

нормированных сферических функций и коэффициентами a nm и Ьnт для

обычных сферических функций, являющиеся обратными к тем, что приведены

в (1 91):