6 Вопрос. Натуральная система координат
Силовые линии и уровенные поверхности создают естественную опору для определения положения в пространстве. При геодезических измерениях приборы почти всегда ориентируют с по-
мощью отвесов и уровней по вектору силы тяжести (отвесной линии), поэтому результаты практически всех измерений зависят от структуры поля силы тяжести. Для определения земной поверхности в большинстве случаев измеряют не просто углы и рассто-
яния между пунктами этой поверхности, а их проекции на повер-хности, ортогональные вектору силы тяжести. Установлено, что через любую точку проходит одна
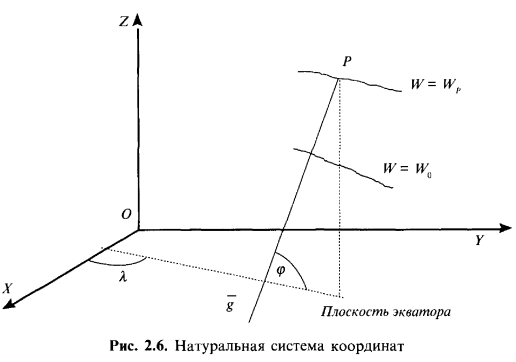
силовая линия и одна уровенная поверхность потенциала силы тяжести, поэтому естественно определять положение точек как пересечение силовой линии и уровенной поверхности. Направлениесиловой линии определяют астрономические координаты широта (р и долгота Я. Астрономическая широта - это дополнение до 90° угла между линией, параллельной оси вращения Земли, и отвесной линией (рис. 2.6). Долгота равна двугранному углу между плоскостями начального астрономического меридиана и астрономического меридиана данной точки. Напомним, что астро-
номическим меридианом называют плоскость, проходящую через отвесную линию и линию, параллельную оси вращения Земли. Силовая линия поля силы тяжести - линия двоякой кривизны, по-этому отвесная линия и ось вращения Земли являются в общем случае скрещивающимися прямыми. Из-за этого астрономический меридиан не проходит через ось вращения Земли.
Напомним также, что астрономическим азимутом а называют угол между плоскостью астрономического меридиана и плоскостью вертикала, содержащей отвесную линию и наблюдаемый
предмет. В геодезии астрономический азимут отсчитывают от направления на север по ходу часовой стрелки.Сложнее обстоит дело с определением третьей координаты,определяющей положение уровенной поверхности, потому что нет методов измерения потенциала. Принципиальную возможность измерения разности потенциалов открывает равенство (1.7): нуж-
но измерить по любому пути между исходной и текущей точками силу тяжести % и расстояние между уровенными поверхностями. Предположим, что от исходного пункта, лежащего на геоиде W=W0 (2.29) проложен нивелирный ход, вдоль которого измерены превышения и сила тяжести g. Тогда в любой точке этого хода можно вычислить геопотенциальное число (1.14).
Триада (р, Я, \¥а IV образует натуральные координаты в поле силы тяжести. В натуральной системе можно определять положение точек непосредственно по измерениям и решать механические задачи, связанные с работой в поле силы тяжести. Однако сложность и, главное,неизвестность формы уровенных поверхностей и силовых линий не позволяет использовать эту систему для решения геометрических задач. Даже задача вычисления расстояния между
двумя точками, определяемыми координатами (рь Яь (IV0 - IV)] и (р2, Я2, ( - становится неразрешимой. Для решения любых геодезических задач вводят более простую систему координат,по возможности близкую к натуральной.
Уравенные поверхности и силовые линии
Геометрически поле силы тяжести можно представить поверхностями постоянного потенциала (эквипотенциальными, или уровенными поверхностями): W(r) = const, (2.33) а также силовыми линиями (рис. 2.6). Связь между изменением величины потенциала и изменением местоположения следует из выражения (2.15) dW = g · dr = gdr(cosg, dr). (2.34)
При перемещении по уровенной поверхности dW:::; О, т.е. никакой работы не со
вершается. Уровенные поверхности являются по~ерхностями равновесия.
Рис. 2.6. Эквипотенциальные поверхности и силовые линии вблизи земной поверхности.
Силовые линии пересекают уровенные поверхности по нормали. Если элементарный отрезок dr совпадает с направлением силовой линии (с направлением внешней нормали n к поверхности), то, поскольку cos (g, dr) = - 1, справедливо соотношение dW .= _ gdп. (2.35)
Так как сила тяжести с перемещением по поверхности Земли изменяется, уровенные поверхности не параллельны; при увеличении силы тяжести они сближаются. Уровенную поверхность, наилучшим образом аппроксимирующую средний уровень Мирового океана, назвали геоидом. Она является одной из отсчетных поверхностей для задания системы высот (разд. 2.5.2).