42.Дифференциальные формулы для фундаментальных постоянных

*Пеллинен Л.П. Высшая геодезия, стр. 146-147(Лебедев на лекциях давал ссылку на этот учебник, но все равно инфа по этому вопросу не полная, но больше нигде нет. В лекциях не нашел).

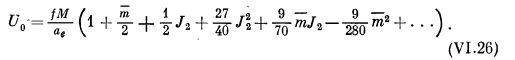
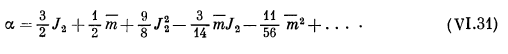
Дифференциальные зависимости между фундаментальными постоянными

Исходя из формулы VI.28, покажем вывод данных зависимостей в виде диференциальных формул. Прологарифмировав и продифференцировав VI.28, получим

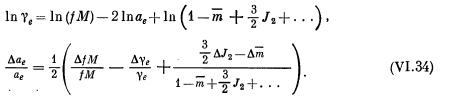
Из формулы VI.7 (см. ниже) имеем:

Относительная точность определения fM, гамма и a в настоящее время несколько выше Угловая скорость подвержена вариациям, которые и ограничивают точность этого параметра. Абсолютная погрешность определения параметра 0,003, а J2 ~ 0,001 можно знаменатель последнего члена в VI.34 принять равным единице. Кроме того, если принять наиболее точные современные выводы параметров

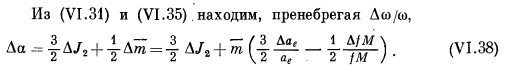
Разъяснения к формулам:fM - см. вопр. 41,α – геометрическое сжатие

- большая полуось эллипсоида; Jе – нормальная сила тяжести на экваторе

Параметры сжатия:

- зональный гармонический коэффициент геопотенциала второй степени

43. Модели Нормальной Земли.

Уровенный эллипсоид, называемый НЗ можно подобрать исходя из пяти параметров перечисленных в вопросе 41.

*Пеллинем «Высшая Геодезия» стр.130

Классификация параметров НЗ.

А. Параметры нулевого порядка

К ним относятся все параметры, которые существовали бы даже если бы НЗ была невращающейся сферой, а ее поле притяжения было центральным:

1. fM;

2. Uo;

3. Гравитационный масштабный множитель

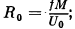
4. Среднее значение норм. СТ на поверхности общеземного эллипсоида

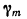
5. Экваториальный радиус Земли ( большая полуось)

6. Экваториальная СТ

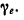
Б. Параметры порядка сжатия

Относятся параметры, имеющие близкий к сжатию порядок:

В. Параметры высших порядков

К ним относятся гармонические коээфициенты нормального потенциала притяжения формуле СТ

44. Система координат в нормальном поле. Связь с геод-й и астрономической ск.

*Все чисто из лекций, так что в основном в виде фоток. Качество нехорошее, так что если у кого есть лекции ищите похожее нечто и учите смело. Больше этого нигде нет, а если есть то видимо он говорил где, а я не слышал.

Нормальное поле задается элипсоидальной нормальной уровенной землей.

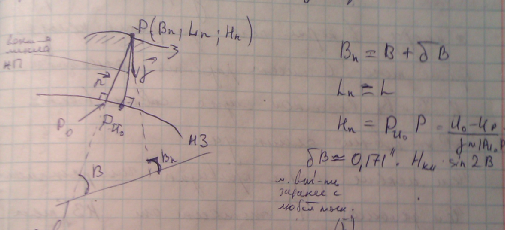
Bn – угол между вектором нормальной СТ (НСТ) в данной точке и плоскостью экватора Нормальной Земли (НЗ).

Плоскость меридиана – плоскость, проведенная через вектор НСТ в данной точке и через ось вращения НЗ.

Ln – угол между вектором НСТ и плоскостью начального меридиана.

- проекция точки P на НЗ по силовой линии.

Система координат(СК) в нормальном поле схожа с геодезической СК относительно общеземного эллипсоида (ОЗЭ), т.е. на геодезическую криволинейную СК.

Ск в НГП очень близка по смыслу к естественной СК(φ,λ,С – геопотенциальное число = Wo – Wр), но есть отличие – координаты в естественной СК м.б. получены из измерений, а координаты в НГП измерить нельзя (НГП – норм. грав. поле.).

Кроме того С имеет размерность потенциала. В и Вn в частном случае совпадают( если P на поверхности эллипсоида).

Чем меньше радиус кривизны, тем расхождения меньше. Чем дальше Р от НЗ, тем расхождения больше.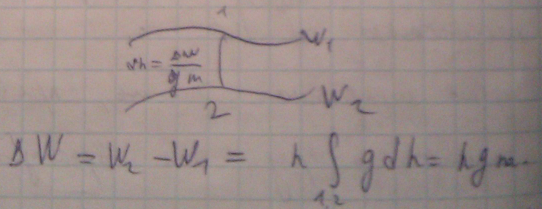

Hn – отрезок дуги, но с очень большой точностью длина дуги равна длине хода.

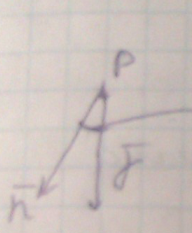СУОЛ гр – состовляющая уклонения отвесной линии гравиметрическая. (на данном рисунке угол и есть уклонение ОЛ).

Т.к. γ близко к исходному астрономо – геодезическому уклонению отвеса, это угол между направлением отвеса в данной точке и нормали к общеземному эллипсоиду. Координаты точки в НГП определяют направляющий косинус вектора γ.

ξ – проекция уклонения отвеса на ось меридиана

η – проекция уклонения отвеса на соотв. параллель?

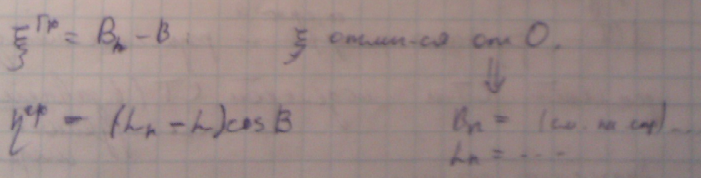
Вывод: если мы знаем координаты в НГП, то мы знаем геодезические координаты в общеземеной СК