23 Плоскость в пространстве. Нормальный вектор плоскости

Ясно, что любая плоскость в пространстве можно определить одним из 2 способов:

1) Точкой Mo(x_o,y_o,z_o) вектором n ={A,B,C} перпендикулярным данной плоскости, который мы будем называть нормалью плоскости.

2) Точками Mo(x,y,z), M₁(x₁,y₁,z₁) и M₂(x₂,y₂,z₂) не лежащими на одной прямой.

Итак, пусть плоскость, определена точкой Mo и n (1 способ)

Найдем уравнение данной плоскости

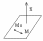
Обозначим через M(x,y,z) произвольную точку плоскости, тогда очевидно, что MoM┴n (ортогональны), а тогда, как известно, скалярное произведение этих векторов=0, т.е. MoM*n=0

Таким образом мы получили векторное уравнение плоскости.

Переходя к координатам полученных векторов получим уравнение плоскости:

A(x-x₀)+B(y-y₀)+C(z-z₀)=0

A_x+By+Cz+D=0 (*)

Таким образом всякая плоскость имеет уравнение вида (*), т.е. каноническое- уравнение плоскости(=определяющее).

Ясно, что коэффициент при x, y и z в каноничном уравнении плоскости дают координаты нормального вектора.

24 Ур-е плоскости, проходящей через три точки. Нормальное уравнение плоскости. Расстояние от точки до палоскости.

Пусть теперь плоскость определена тремя не лежащими на одной прямой точками Mo(x_o,y_o,z_o), M₁(x₁,y₁,z₁), M₂(x₂,y₂,z₂)

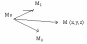Возьмем на этой плоскости M (x,y,z)

Ясно, что вектора MoM₂ MoM₁ и MoM компланарны, а, как известно, условие компланарности этих векторов:

MoM (MoM₁ MoM₂ )=0

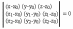Уравнение плоскости: Нормальное (нормированное) уравнение плоскости

в векторной форме:

где  - единичный вектор,   — расстояние П. от начала координат. Уравнение (2) может быть получено из уравнения (1) умножением на нормирующий множитель (знаки   и   противоположны).

Р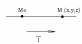 асстояние от точки до плоскости — это наименьшее из расстояний между этой точкой и точками плоскости. Известно, что расстояние от точки до плоскости равно длине перпендикуляра, опущенного из этой точки на плоскость. Расстояние   от точки  , до плоскости, заданной уравнением  , вычисляется по формуле:

25 Прямая в пространстве.

Ясно, что прямую в пространстве можно определить одним из 3-х способов:

1) Точка Mo(x_o,y_o,z_o) принадлежит прямой и l ={m,n,p}параллелен прямой, где l направляющий вектор.

2) Mo(x_o,y_o,z_o), M₁(x₁,y₁,z₁)

3) Пересечением двух плоскостей.

Пусть прямая определена 1-ым способом.

Обозначим через M произвольную точку

Ясно, что вектора MoM и l коллинеарны, т.е. MoM= λ l.

Векторное уравнение прямой.

MoM= λ l

Координатное уравнение (*):

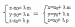
Система (*) называется параметрическим уравнением прямой в пространстве:

m, n, p не равны 0.

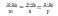каноническое уравнение прямой в пространстве.

Если p=0, то z-z₀ =0

Ясно, что одна или две координаты l могут быть=0. Тогда, например, каноническое уравнение принимает вид:

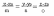, что означает, что z-z₀ =0, и

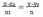
Пусть теперь прямая задается двумя точками Mo(x_o,y_o,z_o) и M₁(x₁,y₁,z₁). Для того, чтобы написать каноническое уравнение прямой надо знать точку, принадлежащею данной прямой (Mo) и направляющий вектор l .

Ясно, что в качестве l можно взять l = MoM = {(x₁-x₀);(y₁-y₀); (z₁-z₀)}

Тогда каноническое уравнение:

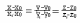
Пусть задается пересечением двух плоскостей:

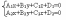
Для нахождения какой-либо (.) принадлежащей данной прямой, как правило, поступают следующим образом: полагают, что одна из координат (например z=0), тогда для нахождения x_o и y₀ полагают:

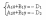Отсюда находят x_o и y_{0 .}

Найдя Mo(x_o,y_o,z_o), остается найти направляющий вектор. Ясно, что в качестве направляющего вектора l можно взять l =n₁ n₂ (векторное произведение нормалей) и после этого записать каноническое уравнение.