1. Линейные операции над матрицами, их свойства

К линейным операциям над элементами множества или пространства относятся операции сложения элементов и их умножения на скаляр (число).  Умножение матрицы на число  При умножении матрицы  A  на число  λ  (слева или справа) каждый ее матричный элемент умножается на это число:

(2)

Сложение матриц  Операция сложения определена только для матриц одинаковых размеров. Результатом сложения матриц  A = || a_i j ||  и  B = || b_i j ||  является матрица  C = || c_i j || , элементы которой равны сумме соответствующих матричных элементов:

(3)

Для любых матриц   одинаковых размеров и любых чисел   справедливы равенства:

1.   (коммутативность сложения);

2.   (ассоциативность сложения);

3. существует нулевая матрица   (тех же размеров, что и  ):  ;

4. существует матрица  , противоположная матрице  ;

5.  ;

6.  ;

7.  ;

8.  .

2.Умножение матриц, основные свойства.

Матрица, получаемая в результате операции умножения, называется произведе́нием ма́триц.

Пусть даны две прямоугольные матрицы   и   размерности   и   соответственно:

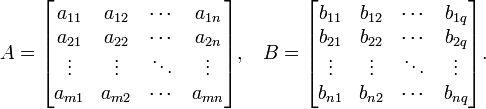
Тогда матрица   размерностью   называется их произведением:

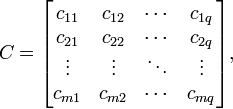
где:

Операция умножения двух матриц выполнима только в том случае, если число столбцов в первом сомножителе равно числу строк во втором; в этом случае говорят, что форма матрицсогласована. В частности, умножение всегда выполнимо, если оба сомножителя — квадратные матрицы одного и того же порядка.

Сочетательное свойство:

Распределительное свойство:

.

Произведение матрицы на единичную матрицу   подходящего порядка равно самой матрице:

Произведение матрицы на нулевую матрицу   подходящей размерности равно нулевой матрице:

Если   и   — квадратные матрицы одного и того же порядка, то произведение матриц обладает ещё рядом свойств.

Умножение матриц в целом некоммутативно:

Если  , то матрицы   и   называются перестановочными или коммутирующими между собой.

Определитель и след произведения не зависят от порядка умножения матриц:

3.Стандартная матрица. Примеры

4.

Понятия линейной зависимости и линейной независимости определяются для строк и столбцов одинаково. Поэтому свойства, связанные с этими понятиями, сформулированные для столбцов, разумеется, справедливы и для строк.

1. Если в систему столбцов входит нулевой столбец, то она линейно зависима.

2. Если в системе столбцов имеется два равных столбца, то она линейно зависима.

3. Если в системе столбцов имеется два пропорциональных столбца  , то она линейно зависима.

4. Система из   столбцов линейно зависима тогда и только тогда, когда хотя бы один из столбцов есть линейная комбинация остальных.

5. Любые столбцы, входящие в линейно независимую систему, образуют линейно независимую подсистему.

6. Система столбцов, содержащая линейно зависимую подсистему, линейно зависима.

7. Если система столбцов   — линейно независима, а после присоединения к ней столбца   — оказывается линейно зависимой, то столбец   можно разложить по столбцам  , и притом единственным образом, т.е. коэффициенты разложения находятся однозначно.

Ранг матрицы — наивысший из порядков миноров этой матрицы, отличных от нуля

Ранг матрицы равен числу ненулевых строк в матрице после приведения её к ступенчатой форме при помощи элементарных преобразований над строками матрицы

5.

Ступенчатая матрица — матрица, имеющая m строк, у которой первые r диагональных элементов ненулевые, r ≤ m, а элементы, лежащие ниже диагонали и элементы последних m − r строк равны нулю:

Ступенчатая матрица, m = 6, n = 4, r = 3:

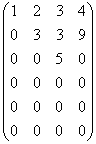
6.

Для того, чтобы матрица А имела обратную, необходимо и достаточно, чтобы ее определитель был отличен от нуля

7.

Определитель (детерминант) квадратной матрицы   — это число  , которое ставится в соответствие матрице и вычисляется по ее элементам согласно следующим правилам.

1. Определителем матрицы   порядка   называется единственный элемент этой матрицы:  .

2. Определителем матрицы  порядка   называется число

(2.1)

где   — определитель квадратной матрицы порядка  , полученной из   вычеркиванием первой строки и j-го столбца.

Определитель матрицы обозначают, заключая матрицу в "прямые" скобки:

Основные свойства определителей.

Свойство 1. Определитель квадратной матрицы не изменяется при еётранспонировании:

Свойство 2. Если одна из строк (столбцов) матрицы целиком состоит из нулей, то её определитель] равен нулю.

Свойство 3. При перестановке местами любых двух строк (столбцов) матрицы её определитель меняет знак.

Свойство 4. При умножении строки (столбца) матрицы на число её определитель умножается на это число.

Свойство 5. Если каждый элемент i-й строки (столбца) матрицы A представлен в виде суммы двух слагаемых, то определитель такой матрицы равен   , где элементыматриц B и C, за исключением элементов i-й строки (столбца), совпадают с соответствующими элементами матрицы A. A в i-х строках (столбцах) матриц B и C стоят упомянутые первые и вторые слагаемые соответственно.

8.

формулу вычисления определителя второго порядка

Определитель второго порядка равен разности произведения элементов, стоящих на главной диагонали, и произведения элементов, стоящих на побочной диагонали (см. схему на рис. 2.1).

формулу вычисления определителя третьего порядка

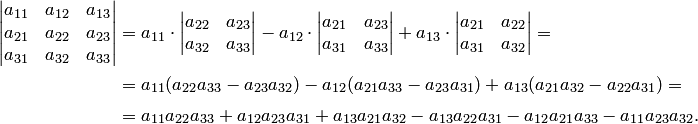
9.

Пусть дана квадратная матрица   порядка  .

Дополнительным минором   элемента   называется определитель матрицы порядка  , полученной из матрицы   вычеркиванием i-й строки и j-го столбца.

Алгебраическим дополнением   элемента   матрицы   называется дополнительный минор   этого элемента, умноженный на 

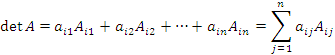 (разложение по i-й строке)

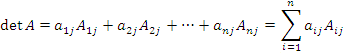разложение по j-му столбцу)

10

Что бы привести матрицу к треугольному виду, нужно воспользоваться методом Гаусса, который является простым в использовании и позволяет быстро прийти к конечному результату. Метод заключается в том чтобы исходную матрицу, путём элементарных преобразований привести к треугольному (ступенчатому) виду.