2. Стандартные функции

2.1 Классификация стандартных функций

Пакет MathCAD является мощной вычислительной системой за счет наличия огромного количества стандартных функций, которые можно классифицировать следующим образом:

1. математические (арифметические, тригонометрические, гиперболические, комплексные, специальные);

2. векторные и матричные (создания, объединения, работы со строками и столбцами, матричная алгебра, специальные функции);

3. статистические (вероятности, гистограммные, распределения);

4. аппроксимация и интерполяция (интерполяция, аппроксимация, регрессия, сплайны, линейное предсказание);

5. решение линейных, нелинейных, дифференциальных уравнений и систем;

6. доступа к внешним данным (ввод/вывод структурированных и неструктурированных файлов).

2.2 Основные элементарные математические функции

Основные элементарные математические функции можно разделить на 6 групп:

1. тригонометрические – sin(z), cos(z), tan(z), cot(z), csc(z), sec(z);

2. гиперболические – sinh(z), cosh(z), tanh(z), coth(z), csch(z), sech(z);

3. обратные – asin(z), acos(z), atan(z);

4. обратные гиперболические – asinh(z), acosh(z), atanh(z);

5. показательные и логарифмические – exp(z), ln(z), log(z);

6. функции комплексного аргумента – Re(z), Im(z), arg(z), CTRL+"–комплексно сопряженное.

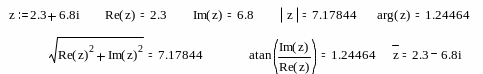Во всех тригонометрических функция аргумент (z) должен быть в радианах, скалярным и безразмерным. Для перевода из градусов в радианы и обратно удобно использовать встроенную переменную deg . Обратные тригонометрические функции возвращают результат в радианах.

2 .3. Основные функции работы с векторами и матрицами

Существует ряд встроенных векторных и матричных функций. Рассмотрим основные, введя следующие обозначения: V – для векторов, M – для матриц.

Функция	Назначение
length(V)	число элементов вектора
last(V)	индекс последнего элемента
max(M), min(M)	максимум, минимум матрицы
Re(M), Im(M)	действительная и мнимая части матрицы
augment(M1,M2)	объединяет в одну матрицу матрицы М1 и М2, имеющие одинаковое число строк (объединение бок о бок)
identity(n)	создает единичную матрицу размером nn
stack(M1,M2)	объединяет две матрицы М1 и М2 имеющие одинаковое количество столбцов, располагая М1 над М2
diag(V)	создает диагональную квадратную матрицу, элементами главной диагонали являются V
submatrix(A,ir,jr,ic,jc)	возвращает подматрицу состоящую из элементов расположенных в строках от ir до jr и столбцах от ic до jc
matrix(m,n,f)	создает матрицу в которой (i, j) – элемент равен f(i, j)
cols(M), rows(M)	число столбцов и строк матрицы
rank(M)	ранг матрицы
tr(M)	след квадратной матрицы (сумма диагональных элементов),
sort(V)	сортировка вектора по возрастанию
reverse(V)	сортировка вектора по убыванию
csort(M,n)	перестановка строк матрицы так, чтобы отсортированным оказался n–й столбец
rsort(M,n	перестановка столбцов матрицы так, чтобы отсортированной оказалась n–я строка