2. Векторы и массивы

Массив – имеющая уникальное имя совокупность конечного числа числовых или символьных элементов, упорядоченных некоторым образом и имеющих определенные адреса. В пакете MathCAD используются массивы двух наиболее распространенных типов: одномерные (векторы), двумерные (матрицы).

Порядковый номер элемента, который является его адресом, называется индексом. Индексы могут иметь только целочисленные значения. Они могут начинаться с нуля или другого целого числа, в соответствии со значением системной переменной ORIGIN. Значение этой переменной может быть переопределено непосредственно в документе, либо с помощью меню Math–Options.

1. векторы и матрицы можно задавать различными способами: с помощью команды Insert – Matrix, комбинации клавиш Ctrl + M, щелчком на кнопке панели Matrix. В появившемся окне задают размерность массива (Columns – столбцы, Rows – строки). Пустые поля заполняют, перемещаясь между ними клавишей Tab. Максимальный размер вводимых таким способом матриц – 10х10, поэтому большие матрицы задают с помощью компоненты Insert – Component – Input Table. Данный компонент вставляет в рабочий документ лист электронной таблицы (подобный листу в Excel). При таком способе ввода матрицы не существует ограничений на ее размер, а использование функций табличного процессора облегчает ввод и просмотр больших массивов, целиком не помещающихся в рабочей области;

2. как переменные с индексами (номер элемента в массиве). Нижний индекс вводится нажатием клавиши [, либо щелчком на кнопке X_n панели Arithmetic. Незаданные элементы по умолчанию задаются нулевыми.;

3. как переменная с индексом, а элементы в массив заносятся перечислением, через запятую;

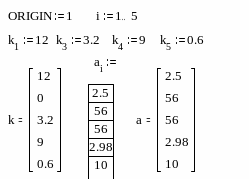4. с использованием дискретного аргумента, когда имеется некоторая явная зависимость для вычисления элементов массива через их индексы.

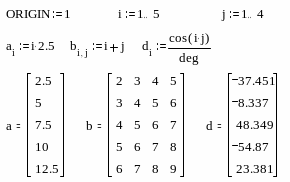Для удобства отображения, громоздкие массивы выводятся в виде электронной таблицы с номерами строк и столбцов и полосами прокрутки. Формат представления данных в таблицах может быть изменен с помощью команды Format–Number– Display as Matrix .

3. Обращение к элементам массива

М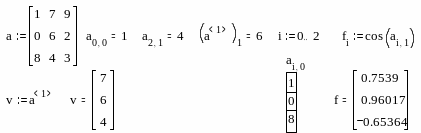 ассивы могут использоваться в выражениях целиком или поэлементно. Для обращения к элементам массивов нужно указать числовые значения индексов элементов. Также можно обращаться к конкретной строке или столбцу матрицы с помощью верхнего индекса (выделения столбца CTRL+^) или нижних индексов.

4. Параллельные вычисления, векторизация.

Большинство вычислений с дискретными переменными и массивами строятся на принципе параллельных (поэлементных) вычислений. Точно такая же операция может быть выполнена с помощью векторизации. Векторизация – проведение некоторой операции над всеми элементами вектора или матрицы.

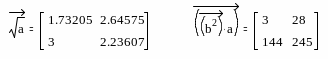
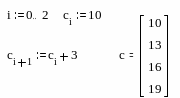
О 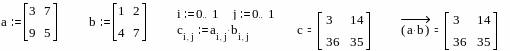перация векторизации позволяет применить математические операции и функции к каждому элементу массива поочередно. Система позволяет выполнять рекуррентные вычисления, когда последующий элемент массива вычисляется через предыдущий по какому либо закону.

Стандартные и пользовательские функции

Функция – выражение, согласно которому проводятся некоторые вычисления с аргументами и определяется её числовое значение.

С ледует особо отметить разницу между аргументами и параметрами функции. Переменные, указанные в скобках после имени функции, являются ее аргументами и заменяются при вычислении функции значениями из скобок. Переменные в правой части определения функции, не указанные скобках в левой части, являются параметрами и должны задаваться до определения функции.

Главным признаком функции является возврат значения, т.е. функция в ответ на обращение к ней по имени с указанием ее аргументов должна возвратить свое значение.

Функции в пакете MathCAD могут быть встроенные (cos, sin, ln), т. е. заблаговременно введенные разработчиками, и определенные пользователем.

Способы вставки встроенной функции:

1. Выбрать пункт меню Insert – Function.

2. Нажать комбинацию клавиш Ctrl + F.

3. Щелкнуть на кнопке .

Пакет MathCAD позволяет расширить систему новыми функциями представляющими интерес для пользователя. Функция пользователя в общем случае имеет вид: Имя_функции(Список аргументов):=Выражение. Имя функции задается как любой идентификатор. Список аргументов функции разделяется запятыми. Аргументы функции являются локальными для неё переменными, поэтому они могут, не определятся до задания функции. Локальные переменные действуют только в выражении, описывающем функцию. При этом их имена могут совпадать с именами глобальных переменных, но при выходе из блока функции значения этих переменных сохраняют ранее заданные значения.

Функции пользователя также могут описываться как локальные, так и глобальные. К сожалению функции пользователя нельзя применять в составе выражений, над которыми осуществляются символьные операции.