Формат вывода числовых данных

При работе с вычислительными областями с помощью команды Format – Number, возможно установить формат вывода числовых данных . Это окно содержит три выделенные части В первой — Radix — устанавливается тип основания чисел Decimal , Hex или Octal.

Вторая часть Precision (точность) — задает погрешность вычислений в виде показателя степени n для числа 10 в этой степени. Задаются число отображаемых знаков Displayed (точность вывода), границы представления чисел в экспоненциальной форме Exponential Threshold (диапазон показателя), допустимая граница для комплексных чисел Complex Tolerance (комплексная точность) и допустимая граница для действительных чисел Zero Tolerance (точность нуля).

О кно для установки формата чисел

В третьей части — Imaginary (мнимая единица) — задается знак мнимой единицы для комплексных чисел i или j. Если Re (Z)/Im (Z) >10n, то комплексное число Z выводится как действительное, а если Im (Z)/Re (Z) >10ⁿ, то число Z выводится как мнимое. Значения n для этих представлений задает параметр Complex Tolerance. Если действительное число больше числа 10 в степени п или меньше, чем 10 в степени – n, где n — значение параметра Exponencial Threshold, то число представляется в экспоненциальной форме. Если значения чисел по модулю меньше указанных параметром Zero Tolerance, числа представляются в виде нулей. Все это особенно важно при научно-технических расчетах, когда излишняя точность представления чисел ни к чему хорошему не ведет

С помощью диалогового окна можно сделать формат глобальным (Global) или локальным (Local). Глобальный формат задает представление для всех числовых данных документа, а локальный — только для текучего блока.

Для массивов чисел их вывод задается в виде матрицы – включением опции Display as Matrix (отображение в виде матрицы). Однако для больших массивов это может быть неприемлемо, так как такая матрица выходит за пределы экрана. Если опция отключена, то большие массивы отображаются как электронные таблицы. Trailig Zeros – включает отображение нулевых младших разрядов.

Структурированные данные

1. Дискретные переменные

Дискретной называется переменная, содержащая несколько значений, каждое из которых отличается от предыдущего на величину постоянного шага и имеющая начальное и конечное значение. Эти переменные имеют два способа определения:

1. Name := Nbegin .. Nend ;

2. Name := Nbegin, (Nbegin + Step) .. Nend.

где Name – имя переменной, Nbegin – ее начальное значение, Nend – конечное значение, ..(; на клавиатуре, либо m..n – в арифметической палитре ) – символ, указывающий на изменение переменной в заданных пределах (вводится клавишей ;). Step –шаг изменения переменной (он должен быть положительным, если Nbegin < Nend, или отрицательным в обратном случае).

Если шаг не указывается (1 способ), то он выбирается равным единице. Если Nbegin < Nend, то шаг переменной будет равен +1, иначе –1.

Д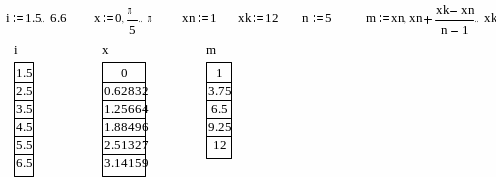 искретные аргументы значительно расширяют возможности MathCAD, позволяя выполнять многократные вычисления или циклы с повторяющимися вычислениями, формировать векторы и матрицы. Параметрами могут быть константы, переменные, выражения.

Функция дискретного аргумента имеет множество значений, каждое из которых соответствует соответствующему значению дискретного аргумента. Дискретная переменная может являться аргументом функции пользователя или индексом для организации одномерных и двумерных массивов.