6.1 Регрессия функций

Регрессия – представление совокупности данных некоторой функцией f(x). Задачей регрессии является вычисление параметров функции f(x) таким образом, чтобы функция приближала "облако" исходных точек с наименьшей погрешностью. При этом функция f(x) называется уравнением регрессии. При регрессии не требуется чтобы функция проходила через все заданные точки, что особенно важно при аппроксимации данных, заведомо содержащих ошибки.

Линейная регрессия

Линейная регрессия является простейшим видом регрессии. Классическим алгоритмом линейной регрессии является метод наименьших квадратов. В котором критерием является минимизация суммы квадратов отклонений аппроксимирующей функции от заданных точек:

.

Существуют и другие алгоритмы определения коэффициентов линейной регрессии – метод медиан.

В общем виде аппроксимирующею функцию можно представить как . Задачей линейной регрессии является вычисление параметров a и b. Для этого в MathCad существует ряд встроенных функций (где VX, VY – вектора узловых точек):

1. corr(VX, VY) – возврящает скаляр – коэффициент корреляции Пирсона. Чем ближе коэффициент к 1 тем точнее исходная зависимость приближается к линейной;

2. intercept(VX, VY) – возвращает значение параметра а (свободный член) рассчитанного методом наименьших квадратов;

3. slope(VX, VY) – определяет значение параметра b (угловой коэффициент) рассчитанного методом наименьших квадратов;

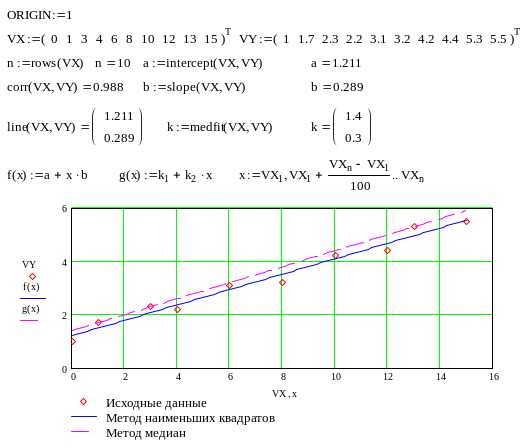
4. line(VX, VY) – [MathCAD 2000] возвращает вектор первый элемент которого параметр а, второй b рассчитанные по методу наименьших квадратов;

5. medfit(VX, VY) – [MathCAD 2000] возвращает вектор первый элемент которого параметр а, второй b рассчитанные по методу медиан.

Как видно из примера при аппроксимации линейной регрессией прямая проходит через "облако" точек.

Используя встроенные функции можно рассчитывать регрессию не только для линейных, но и для экспоненциальных функций . Для этого f(x) с помощью логарифмирования по натуральному основанию приводится к линейной. Рассчитанный коэффициент а, полученный в логарифмической форме, затем пересчитывается.

Л инейная регрессия общего вида

MathCAD позволяет проводить линейную регрессию общего вида, в которой аппроксимирующая функция задается линейной комбинацией функций, причем сами фикции f_i(x) могут быть не линейными:

.

Л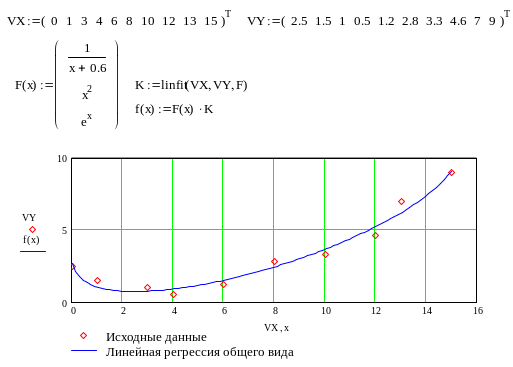 инейная регрессия общего вида реализуется с помощью функции linfit(VX, VY,F) – возвращающей вектор коэффициентов К, при котором среднеквадратичная погрешность приближения "облака" исходных точек с координатами VX, VY, минимальна. Вектор F содержит функции f_i(x) записанные в символьном виде. Вектор VX должен быть возрастающим.

Полиномиальная регрессия

Полиномиальная регрессия позволяет аппроксимировать зависимость полиномом произвольной степени. Вычисление коэффициентов полинома осуществляется с помощью встроенной функции regress(VX, VY,n), где VX, VY – вектора с координатами исходных данных, n – порядок полинома (первые три возвращаемые коэффициенты служебные, а далее искомые значения расположенные по возрастанию степени полинома). Для построения аппроксимирующей зависимости можно воспользоваться либо встроенной функцией interp(VK,VX, VY,x), либо функцией , где VK – вектор коэффициентов расчитанных функцией regress; x – рассчитываемая точка. Для проведения регрессии необходимо что бы вектор VX был возрастающим и его количество его элементов было больше степени полинома на 1.

Ф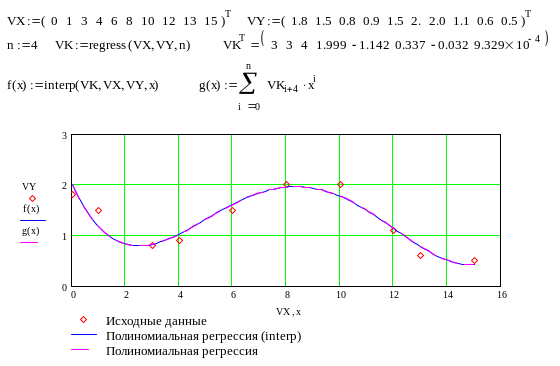 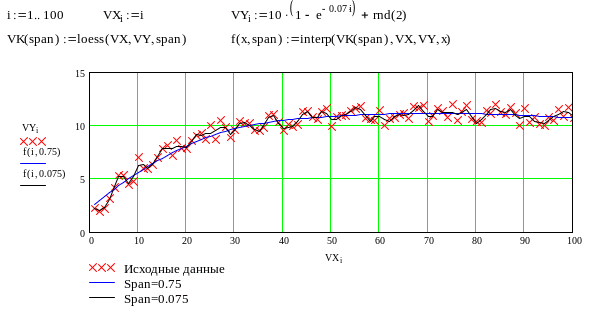ункция regress определяет единственный приближающий полином, элементы которого вычисляются по всей совокупности точек. Для проведения локальной регрессии используется функция loess(VX, VY,span) – дающая приближение отрезками полиномов второй степени, где span – величина задающая длину отрезков. Чем больше величина span>0, тем сильнее сглаживаются данные. Чем меньше шаг между точками VX, тем меньше должно быть span. При больших значениях span функция приближается к regress(VX, VY,2). Рекомендуемое значение 0.75, однако оно подходит далеко не всегда и требует уточнения.