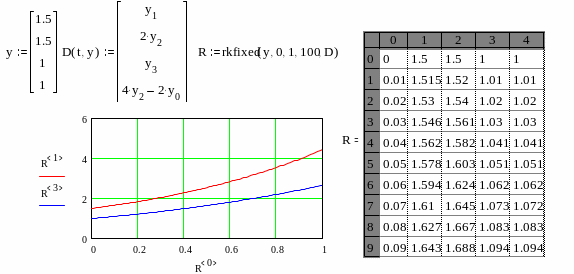
Рекомендации по использованию

Обычно функция Rkadapt благодаря автоматическому изменению шага решения дает более точный результат, но по скорости вычислений она проигрывает функции rkfixed, хотя если решение меняется медленно, она может привести к заметному уменьшению числа вычислений. Поэтому функция Rkadapt наиболее пригодна для решения ОДУ дающих медленно меняющееся решения.

Примеры решения дифференциальных уравнений

1. Решим ОДУ .

1. Задаем вектор начальных условий:

2. З 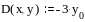адаем вектор – функцию первой производной неизвестной функции:

3. Для решения воспользуемся функцией rkfixed :

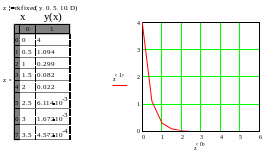
1. Решим дифференциальное уравнение второго порядка:

.

Преобразуем уравнение в систему ОДУ первого порядка, решенных относительно первой производной:

.

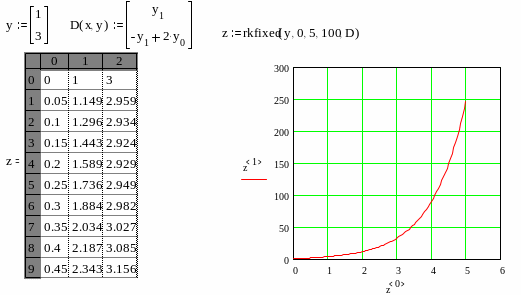
3. Решим систему линейных уравнений первого порядка:

.

4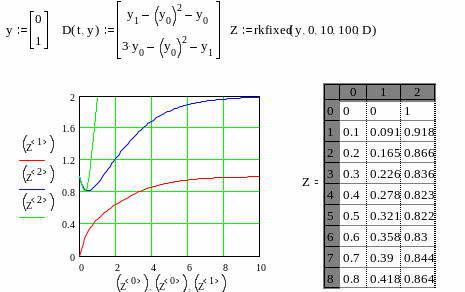 . Решим систему двух линейных уравнений второго порядка:

с начальными условиями .

5. Программирование в пакете Mathcad

Система Mathcad позволяет задавать функции пользователя используя встроенный язык программирования, что позволяет значительно расширить область применения пакета. Перед тем как использовать программу-функцию нужно ее задать – выполнить описание.

Порядок описания программы–функции Mathcad:

1. ввести имя программы-функции и список формальных параметров.

имя_программы (формальные параметры: =);

2. в панели Programming, выбрать Add line. На экране появится вертикальная черта и вертикальный столбец с двумя полями ввода для ввода операторов, образующих тело программы-функции;

3. в поле 1 (щелкнув на нем мышью или нажав клавишу [Tab]) ввести первый оператор тела программы-функции. Для вставки дополнительных полей ввода нажать на кнопке Add line;

4. в последнем поле (поле 2), определить возвращаемое через имя программы-функции значение ( см. рис.).

Рис. Структура программы–функции

В качестве примера определим функцию перевода из радиан в градусы:

Д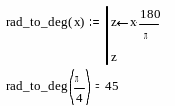 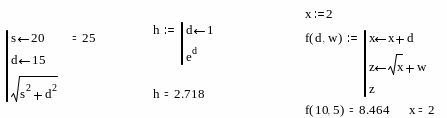ля выполнения программы-функции необходимо обратиться к её имени с указанием списка фактических параметров. Фактические параметры указывают при каких конкретных значениях осуществляются вычисления в теле программы. Между фактическими и формальными параметрами должно быть соответствие по количеству, порядку следования и типу. Программный модуль может вести себя и как функция без имени и параметров, но обязательно возвращающий результат.

Переменные определенные в функции являются локальными. Как видно из последнего примера локальное изменение переменной х в программе–функции, не привело к изменению внешней переменной х.

Основные программные операторы

Для создания программных модулей используются следующие основные элементы:

Название	Описание
Add Line	Создание и расширение программного модуля;
	Внутреннее локальное присваивание.
if	Оператор условного выражения. Общий вид: выражение if условие. В случаи выполнения условия возвращается значение выражения. Совместно с этим оператором часто используются break и otherwise.
for	Wиклов с заданным числом повторений. Общий вид: for Var Nmin..Nmax. Цикл можно задать диапазоном, множеством, вектором, возможна их комбинация. Переменную цикла Var можно использовать в программе.
while	Цикл с предусловием, действующий пока условие истинно. Общий вид: while условие. Тело цикла записывается на месте шаблона.
otherwise	Оператор "иначе", обычно используется совместно с if для выполнения действий в случаи не выполнения условия.
break	Вызывает прерывание работы программного блока. Обычно используется с операторами циклов и условия, для досрочного выхода из цикла или программного блока.
continue	Используется для продолжения работы цикла после прерывания. Обычно используется совместно с операторами задания циклов, обеспечивает прерывание и возврат в начало цикла.
return	Прерывает выполнение программы и возвращает значение своего операнда.
on error	Оператор обработки ошибок. Общий вид: выражение1 on error выражение2. Если при выполнении выражения1 возникла ошибка, то выполняется выражение2. Для обработки ошибок полезна функция error(S), которая выдает текстовое сообщение (S) и прерывает работу программного блока.