Отсутствие сходимости решения

Сообщение об ошибке (Решение не найдено) при решении уравнений появляется, когда:

1. система не имеет решения;

2. для уравнения, которое не имеет вещественных решений, в качестве начального приближения взято вещественное число и наоборот;

3. в процессе поиска решения последовательность приближений попала в точку локального минимума невязки. Для поиска искомого решения нужно задать различные начальные приближения;

4. возможно, поставленная задача не может быть решена с заданной точностью. Попробуйте увеличить значение TOL.

Приближенные решения

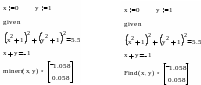Функция Minerr очень похожа на функцию Find (использует тот же алгоритм). Если в результате поиска не может быть получено дальнейшее уточнение текущего приближения к решению, Minerr возвращает это приближение. Функция Find в этом случае возвращает сообщение об ошибке. Правила использования функции Minerr такие же, как и функции Find. Общий вид Minerr Minerr(z1, z2, ...). Число аргументов должно быть равно числу неизвестных. При использовании Minerr используется в блоке решения уравнений, необходимо всегда включать дополнительную проверку достоверности результатов.

Решение матричных уравнений

Система n линейных алгебраических уравнений относительно n неизвестных х1, х2, …, хn может быть записана в матричном виде ах=b где: .

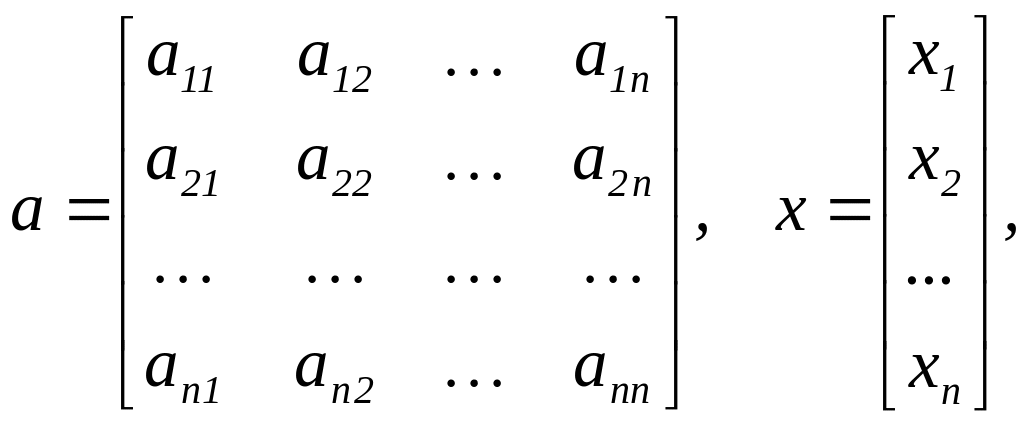
Если матрица а – неособенная, то есть det(а)  0 то система, имеет единственное решение. Для решения систем линейных уравнений можно использовать общепринятые математические методы: метод Крамера, матричный метод и т.д.

Системы линейных уравнений удобно решать с помощью функции lsolve(а, b) – где а – матрица коэффициентов (не сингулярная), b – вектор свободных членов.

4 .3 Решение дифференциальных уравнений и систем Основные функции

Для решения дифференциальных однородных дифференциальных уравнений (ОДУ) – с начальными условиями пакет Mathcad имеет ряд встроенных функций:

1. rkfixed – функция решения ОДУ и систем ОДУ методом Рунге–Кутта четвертого порядка с постоянным шагом;

2. Rkadapt – функция решения ОДУ и систем ОДУ методом Рунге–Кутта с переменным шагом;

3. Bulstoer –функция решения ОДУ и систем ОДУ методом – метод Булирша–Штёра если заранее известно, что решением является гладкая функция.

Рассмотрим подробнее каждую из этих функций:

1. rkfixed(y, x1, x2, p, D) – возвращает матрицу первый столбец которой содержит точки, в которых получено решение, а остальные столбцы – решения, первые n-1 производные. Функция возвращает матрицу, состоящую из 1+n строк. Аргументы функции: y – вектор начальных условий (k элементов); x1 и x2 – границы интервала, на котором ищется решение ОДУ; p – число точек внутри интервала (x1, x2), в которых ищется решение; D – вектор, состоящий из k элементов, который содержит первые производные искомой функции.

2. Rkadapt(y, x1, x2, p, D) – назначение параметров то же, что и для функции rkfixed. Существует несколько модифицированная функция rkadapt(y,x1,x2, acc,p,D,k,s) – где добавлены параметры k – максимальное число промежуточных точек решения; s – минимально допустимый интервал между точками; acc – погрешность решения (рекомендуется порядка 0.001).

3. Bulstoer(y, x1, x2, p, D) – назначение параметров то же, что и для функции rkfixed.