Мат анализ

№1Рациональные и иррациональные числа. С чётность множества рациональных чисел и

несчетность множества вещественных чисел.

Рациональные числа - это числа вида m/n, где m - целое число, а n - натуральное число. Множество рациональных чисел принято обозначать Q. Иррациональное число - это бесконечная десятичная непериодическая дробь.

№2.Определение предела последовательности.

3. Свойства пределов, связанные с арифметическими операциями над

последовательностями.

3.5. Свойства пределов, связанные с арифметическими операциями над последовательностями 41стр

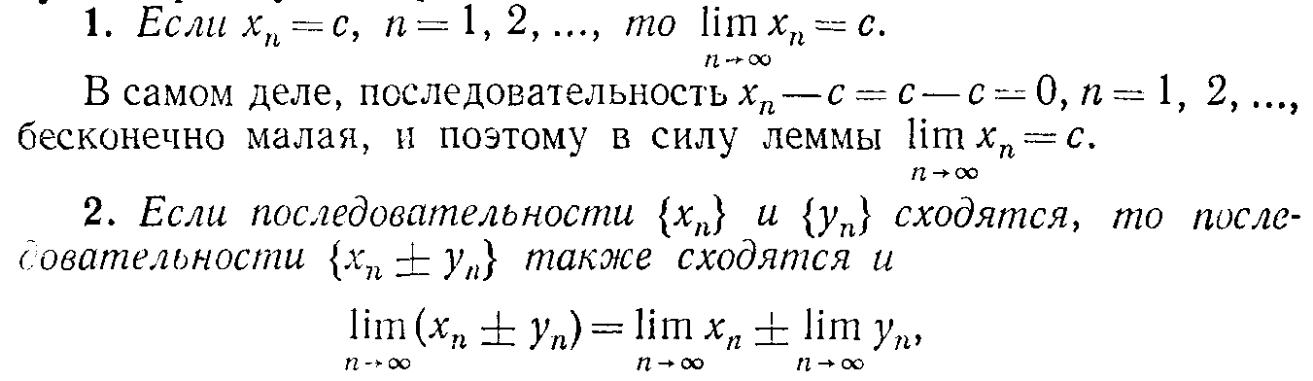
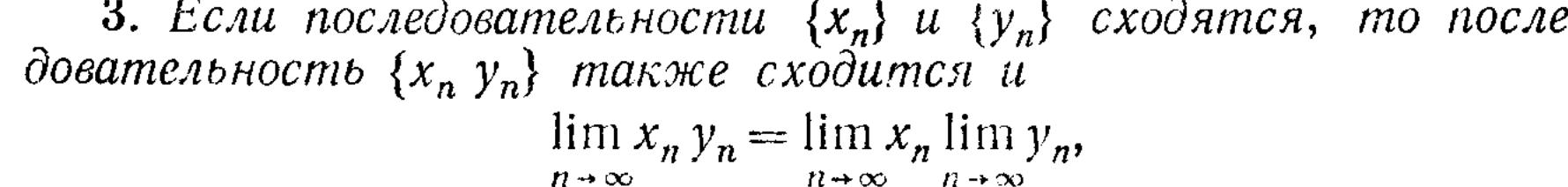
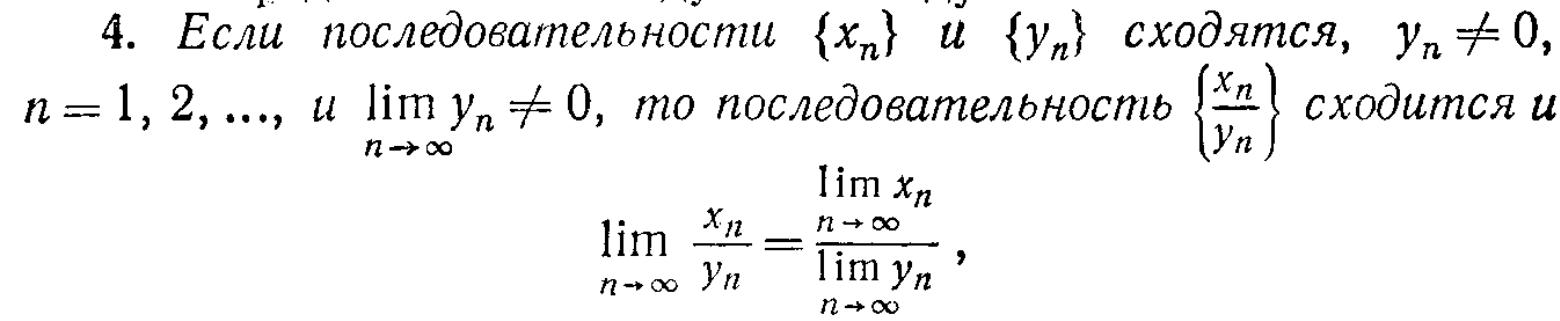
4. Ограниченные и монотонные последовательности.

5. Число e .

e — математическая константа, основание натурального логарифма, трансцендентное число. Иногда число e называют числом Эйлера или числом Непера. Обозначается строчной латинской буквой «e». e ≈ 2,7182818284...

Число e играет важную роль в дифференциальном и интегральном исчислении, а также во многих других разделах математики.

(второй замечательный предел).

6. Бесконечно малые и бесконечно большие последовательности.

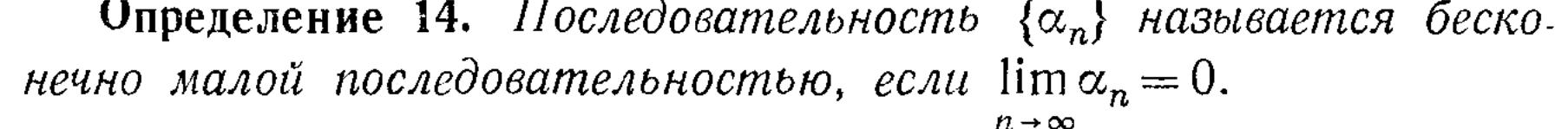
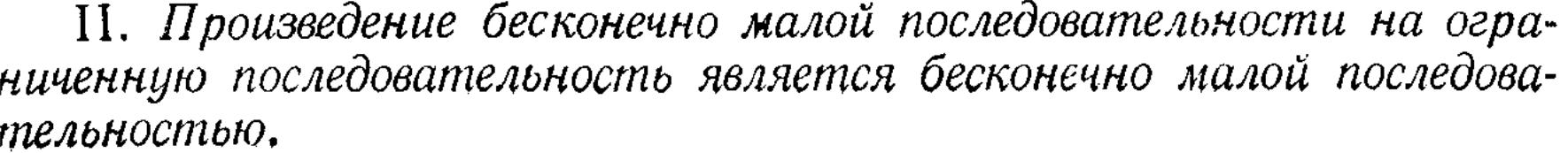
7. Два определения предела функции.

8. Свойства пределов функции.

9. Бесконечно малые и бесконечно большие функции.

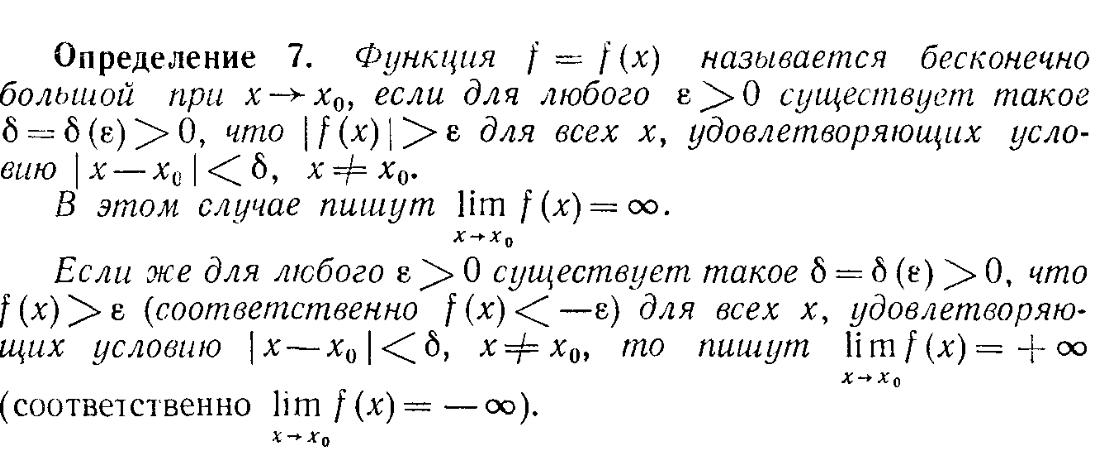
10.Непрерывность функции в точке. Непрерывность элементарных функций.

11.. Замечательные пределы.

Замеча́тельные преде́лы — термин, использующийся в советских и российских учебниках по математическому анализу для обозначения некоторых широко известных математических тождеств со взятием предела. Особенно известны:

Первый замечательный предел:

Второй замечательный предел:

13. Определение производной. Геометрический и физический смыслы производной.

геометрический смысл

Физически смысл.

14. Правила вычисления производных, связанные с арифметическими действиями над

функциями.

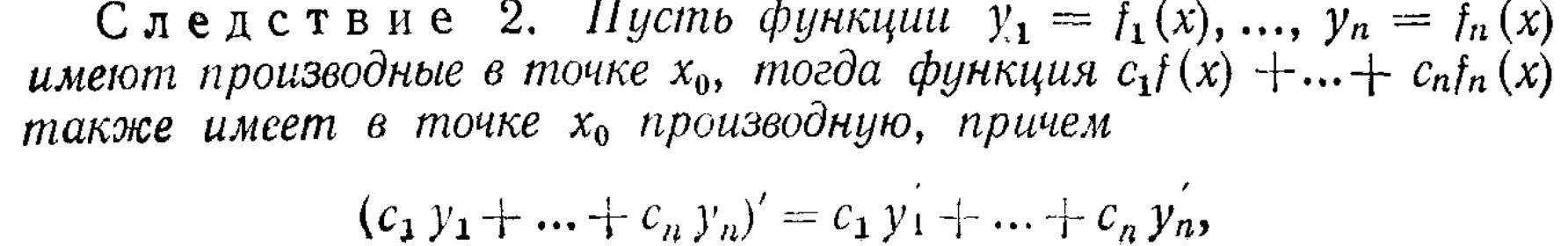
15. Производная обратной функции. Производная сложной функции.

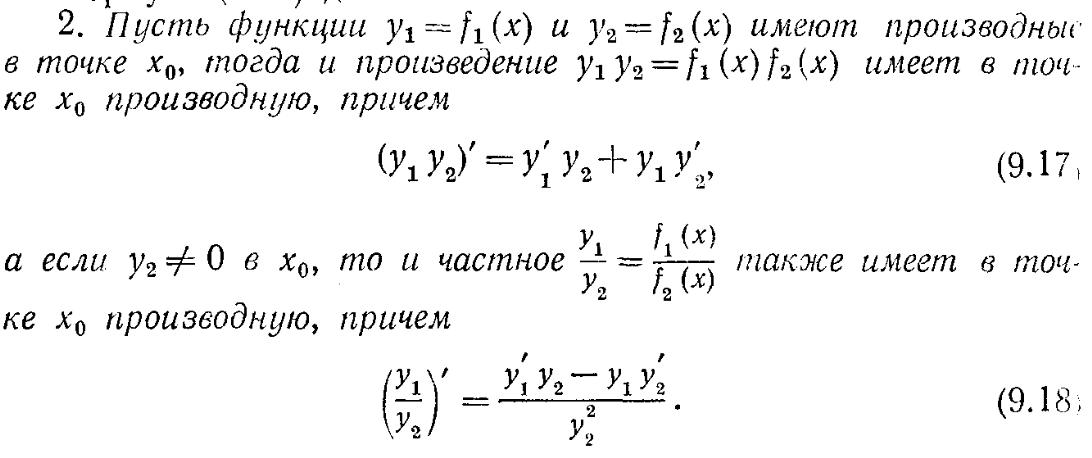
16. Дифференциал функции.

Дифференциал функции

В высшей математике очень часто используется понятие - дифференциал функции. В основном понятием дифференциал функции оперируют в неопределенных интегралах, дифференциальных уравнениях.

Для решения неопределенных интегралов используются различные способы сведения исходных неопределенный интегралов к уже существующим и известным. При этом будет использоваться понятие дифференциала функции, это понятие из дифференциального анализа. Напомним основное определение дифференциала функции.

Определение. Дифференциалом функции (обозначается через ) называется следующее выражение:

где dx -- дифференциал x при условии, что функция имеет производную.

Предположим, что существует следующее равенство функций:

тогда дифференциал от равенства есть

Для решения дифференциальных уравнений используют много разных способов: метод разделения переменных, метод вариации и т.д.

Например, в методе разделения переменных используется определение дифференциала функции т.е.

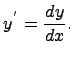
Также это определение используется во многих других методах.

17.Формула Тейлора. Остаточный член в форме Пеано. Формула Маклорена. Примеры

разложения по формуле Тейлора. Вычисление пределов с помощью формулы Тейлора. Xx

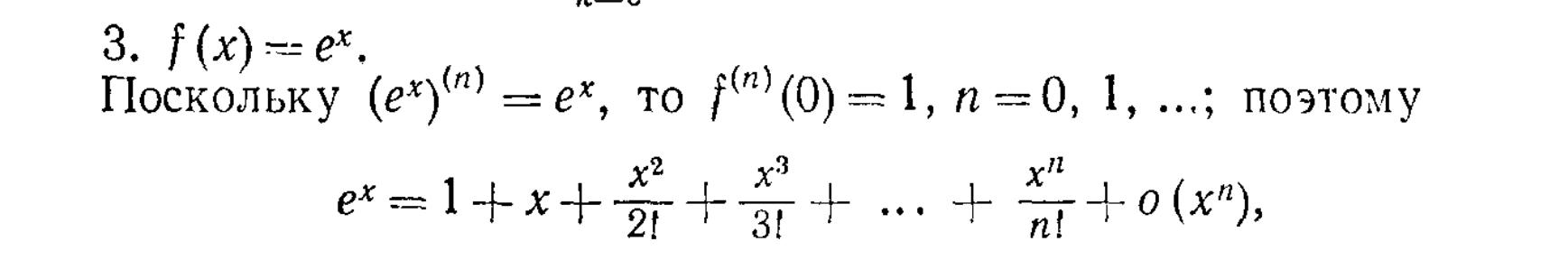
18. Раскрытие неопределенностей по правилу Лопиталя.

Теорема (правило Лопиталя). Пусть функции f(x) и g(x) дифференцируемы в некоторой окрестности точки a, за исключением, быть может, самой точки a, и пусть

или . Тогда, если существует предел отношения производных этих функций , то существует и предел отношения самих функций f(x)/g(x) при x→а, причем

1. 

2. 

19. Определение наибольших и наименьших значений функций.

Следует отметить, что наибольшее и наименьшее значение функции обычно ищется на некотором интервале X, который является или всей областью определения функции или частью области определения. Сам интервал X может быть отрезком , открытым интервалом , бесконечным промежутком .

В этой статье мы будем говорить о нахождении наибольшего и наименьшего значений явно заданной функции одной переменной y = f(x).

Кратко остановимся на основных определениях.

Наибольшим значением функции y = f(x) на промежутке X называют такое значение , что для любого справедливо неравенство .

Наименьшим значением функции y = f(x) на промежутке X называют такое значение , что для любого справедливо неравенство .

Эти определения интуитивно понятны: наибольшее (наименьшее) значение функции – это самое большое (маленькое) принимаемое значение на рассматриваемом интервале при абсциссе .

Стационарные точки – это значения аргумента, при которых производная функции обращается в ноль.

Для чего нам стационарные точки при нахождении наибольшего и наименьшего значений? Ответ на этот вопрос дает теорема Ферма. Из этой теоремы следует, что если дифференцируемая функция имеет экстремум (локальный минимум или локальный максимум) в некоторой точке, то эта точка является стационарной. Таким образом, функция часто принимает свое наибольшее (наименьшее) значение на промежутке X в одной из стационарных точек из этого промежутка.

Алгоритм нахождения наибольшего и наименьшего значения непрерывной функции на отрезке [a; b].

Находим область определения функции и проверяем, содержится ли в ней весь отрезок [a; b].

1. Определяем все стационарные точки, попадающие в отрезок [a; b]. Для этого, находим производную функции, приравниваем ее к нулю, решаем полученное уравнение и выбираем подходящие корни.

2. Если стационарных точек нет или ни одна из них не попадает в отрезок, то переходим к следующему пункту.

3. Вычисляем значения функции в отобранных стационарных точках (если таковые имеются), а также при x = a и x = b.

4. Из полученных значений функции выбираем наибольшее и наименьшее - они и будут искомыми.

Найти наибольшее и наименьшее значение функции

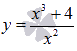
на отрезке [1; 4]

на отрезке [-4; -1]

Решение.

Областью определения функции является все множество действительных чисел, за исключением нуля, то есть . Оба отрезка попадают в область определения.

Находим производную функции по правилу дифференцирования дроби:

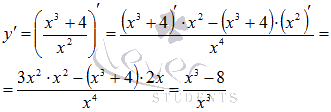
Стационарные точки определим из уравнения . Единственным действительным корнем является x = 2. Эта стационарная точка попадает в первый отрезок [1; 4].

Для первого случая вычисляем значения функции на концах отрезка и в стационарной точке, то есть при x = 1, x = 2 и x = 4:

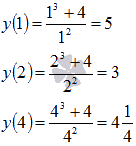
Следовательно, наибольшее значение функции достигается при x = 1, а наименьшее значение – при x = 2.

20. Выпуклость и точки перегиба.

Вторая производная. Если производная f ' ( x ) функции f ( x ) дифференцируема в точке ( x0 ), то её производная называется второй производной функции f ( x ) в точке ( x0 ), и обозначается f '' ( x0 ).

Функция f ( x ) называется выпуклой на интервале ( a, b ), если её график на этом интервале лежит ниже касательной, проведенной к кривой y = f ( x ) в любой точке ( x0 , f ( x0 ) ), x0 ( a, b ).

Функция f ( x ) называется вогнутой на интервале ( a, b ), если её график на этом интервале лежит выше касательной, проведенной к кривой y = f ( x ) в любой точке ( x0 , f ( x0 ) ), x0 ( a, b ).

Достаточное условие вогнутости ( выпуклости ) функции.

Пусть функция f ( x ) дважды дифференцируема ( имеет вторую производную ) на интервале ( a, b ), тогда:

если f '' ( x ) > 0 для любого x ( a, b ), то функция f ( x ) является вогнутой на интервале ( a, b );

если f '' ( x ) < 0 для любого x ( a, b ), то функция f ( x ) является выпуклой на интервале ( a, b ) .

Точка, при переходе через которую функция меняет выпуклость на вогнутость или наоборот, называется точкой перегиба. Отсюда следует, что если в точке перегиба x0 существует вторая производная f '' ( x0 ), то f '' ( x0 ) = 0.

П р и м е р . Рассмотрим график функции y = x3 :

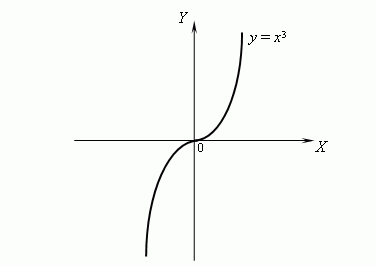
Эта функция является вогнутой при x > 0 и выпуклой при x < 0. В самом деле, y'' = 6x, но 6x > 0 при x > 0 и 6x < 0 при x < 0, следовательно, y'' > 0 при x > 0 и y'' < 0 при x < 0, откуда следует, что функция y = x3 является вогнутой при x > 0 и выпуклой при x < 0. Тогда x = 0 является точкой перегиба функции y = x3.