22. Каноническая совокупность множеств ситуаций.

Основная идея SLR-метода состоит в том, чтобы вначале построить на базе грамматики детерминированный конечный автомат для распознавания активных префиксов. Группируем пункты в множества, которые приводят к состояниям SLR-анализатора. Пункты могут рассматривается как состояния недетерминированного конечного автомата, распознающего активные префиксы.

Операция замыкания. Если I- множество пунктов грамматики G, то closure(I) – множество пунктов, построенное из I по следующим правилам: 1) В замыкание closure(I) заносится множество ситуаций I. 2) Если ситуация [AB] уже принадлежит closure(I) и есть продукция B, то добавляем в closure(I) ситуацию [B].Применяем это правило до тех пор, пока не внесем все возможные пункты в closure(I)

Наличие AB в closure(I) указывает, что в некоторый момент в процессе синтаксического анализа мы полагаем, что можем встретить во входном потоке подстроку, выводимую из B. Но если имеется продукция B, то, естественно, мы также можем встретить в этот момент строку, выводимую из , поэтому включаем B в closure(I)

Любое множество можно разделить на два класса: 1) Базисные пункты включающие начальный пункт S’ -> *S и все пункты, у которых точки расположены не у левого края. 2) Небазисные пункты, у которых точки расположены слева.

Переходы по функции (goto (I,x)) представляет собой множество ситуаций, в которые можно перейти из множества ситуаций I по грамматическому символу х, то есть по терминалу или нетерминалу. При выполнении функции (goto (I,x)) строят замыкание множества состояний вида [Ax], если в I есть ситуация [Ax], то есть точка переходит за символ х в ситуациях. После этого строиться замыкание этого множества.

Используя функции closure(I) и goto(I,x) можно построить каноническую совокупность всех возможных множеств ситуаций дополненной грамматики. Для этого строят замыкание для ситуации [SS]. После этого в цикле находят все множества ситуаций, в которые можно перейти из уже найденного множества по любому грамматическому символу. Цикл завершается, когда нельзя ничего нового добавить в каноническую совокупность.

34. Автомат с магазинной памятью. Допустимость по заключительному состоянию и по пустому магазину.

А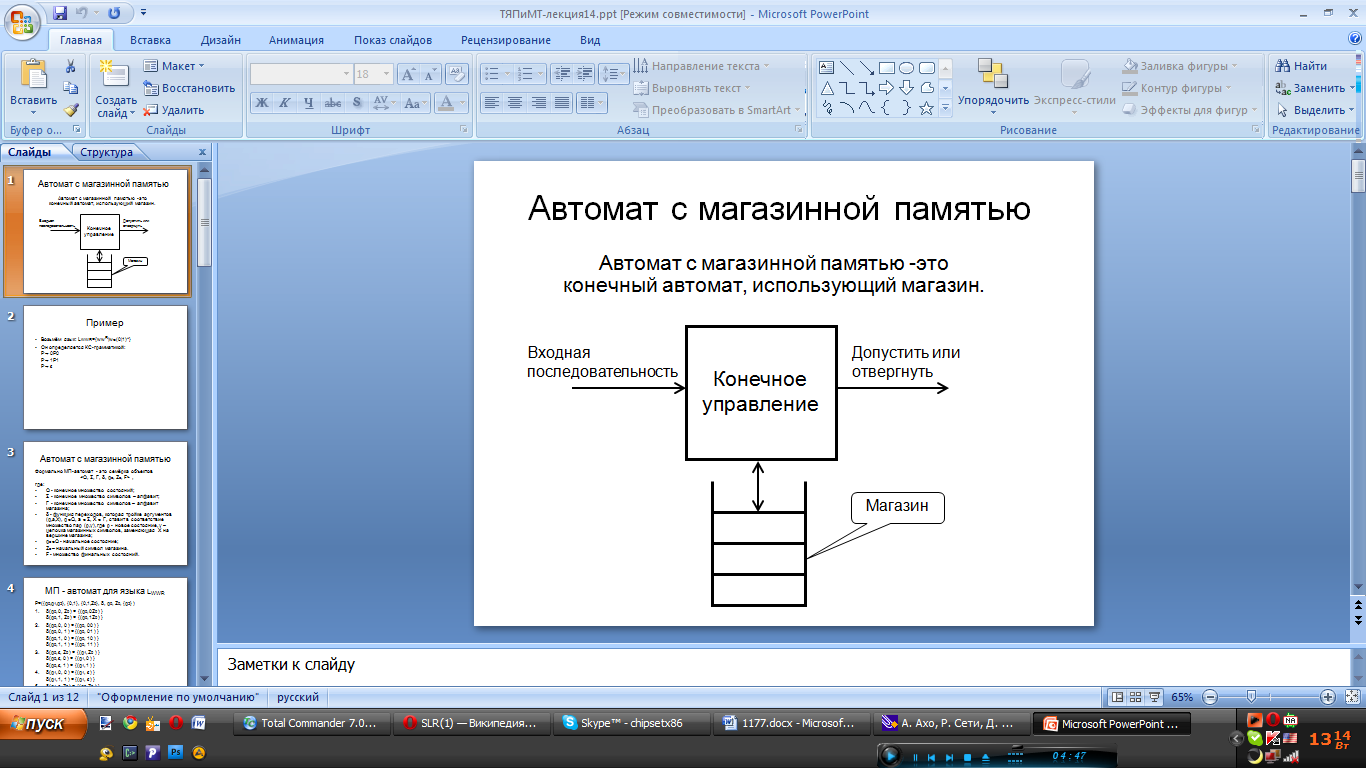 втомат с магазинной памятью – это недерменированный конечный автомат с έ-переходами и одним дополнением – магазин, в котором хранится цепочка “магазинных символов”. Магазинный автомат может обозревать символ на вершине магазина и совершать переход нм основе текущего состояния, входной символ и символ на вершине магазина. Он может выполнить спонтанный переход, используя έ в качестве входного символа. За один такт автомат совершает следующие действия: 1) прочитывает и пропускает входной символ. Если в качестве входа έ, то входные символы не пропускаются. Переходит в новое состояние, которое может и не отличаться от предыдущего 3) Заменяет символ на вершине магазина некоторой цепочкой. Цепочкой может быть έ, что соответствует снятию с вершины магазина, т.е магазин не измениться. Автомат может заменить магазинный символ на один или несколько.

Формально МП-автомат - это семёрка объектов <Q, Σ, Г, δ, q₀, Z₀, F> где Q - конечное множество состояний; Σ - конечное множество символов – алфавит; Г - конечное множество символов – алфавит магазина; δ - функция переходов, которая тройке аргументов (q,a,X), q ∈Q, a ∈ Σ, X ∈ Г, ставит в соответствие множество пар (p,γ), где p - новое состояние, γ – цепочка магазинных символов, заменяющая X на вершине магазина; q₀ ∈Q - начальное состояние; Z₀ – начальный символ магазина.

F - Множество финальных состояний.

Допустимость. Первый способ определения МП-а допускает свой вход, прочитывая его и достигая заключительного состояния. Существует способ определения МП-а, при котором мы может определить язык допускаемый по пустому магазину, т.е множество цепочек, приводящих МП-а в начальной конфигурации к опустошению магазина. Эти два метода эквиваленты в том смысле, что для языка L найдется МП-а допускающий его по заключительному состоянию тогда и только тогда, когда для L найдется МП-а, допускающий его по пустому магазину.

По состоянию: Пусть P= <Q, Σ, Г, δ, q₀, Z₀, F> - МП-а, тогда L(P) – язык, допускаемый P по заключительному состоянию определяется так: {w | (q₀ w, Z₀ ) } |-* (q, έ, α)} для некоторого состояния q из F и произвольной магазинной цепочки α. Таким образом начиная со стартовой конфигурации с w на входе, P прочитывает w и достигает допускающего состояния. Содержимое магазина при этом не имеет значения. По магазину: Пусть P - МП-а, тогда N(P) {N – пустой магазин} – язык, допускаемый P по пустому магазину определяется так: N(P) = {w| (q₀ w Z₀) |-* (q, έ, έ)} где q – любое состояние. Таким образом N(P) представляет собой множество входов w, которые P может прочитать, одновременно опустошив магазин.