37. Lr(1) анализ. Заполнение таблиц lr-разбора

В названии LR(1) символ L указывает на то, что входная цепочка читается слева-направо, R - на то, что строится правый вывод, наконец, 1 указывает на то, что анализатор видит один символ непрочитанной части входной цепочки.

LR(1)-анализ привлекателен по нескольким причинам:

• LR(1)-анализ - наиболее мощный метод анализа без возвратов типа сдвиг-свертка;

• LR(1)-анализ может быть реализован довольно эффективно;

• LR(1)-анализаторы могут быть построены для практически всех конструкций языков программирования;

• класс грамматик, которые могут быть проанализированы LR(1)-методом, строго включает класс грамматик, которые могут быть проанализированы предсказывающими анализаторами (сверху-вниз типа LL(1)).

Рассмотрим теперь алгоритм конструирования таблицы, управляющей LR(1)-анализатором.

Пусть G = (N, T, P, S) - КС-грамматика. Пополненной грамматикой для данной грамматики G называется КС-грамматика

т.е. эквивалентная грамматика, в которой введен новый начальный символ S' и новое правило вывода S' S.

Это дополнительное правило вводится для того, чтобы определить, когда анализатор должен остановить разбор и зафиксировать допуск входа. Таким образом, допуск имеет место тогда и только тогда, когда анализатор готов осуществить свертку по правилу S' S.

LR(1)-ситуацией называется пара [A * , a], где A - правило грамматики, a - терминал или правый концевой маркер $. Вторая компонента ситуации называется аванцепочкой.

Построения таблиц Action и GOTO

Для каждого состояния i из канонической системы функции action[i,A] и goto[i,X] строятся по множеству ситуаций Ii:

1. Значения функции действия (Action) для состояния i определяются следующим образом:

если [A-> α*aβ, b] принадлежит Ii (a - терминал) и goto(Ii, a)= Ij , то полагаем Action[i, a] = shift j;

если [A-> α*, a] причем A неравно S', то полагаем Action[i, a] = reduce A -> α ;

если [S' -> S*,$] принадлежит Ii , то Action[i, $] = accept

2. Значения функции переходов для состояния i определяются следующим образом: если goto(Ii, A) = Ij , то Goto[i, A] = j (здесь A - нетерминал).

3. Все входы в Action и Goto, не определенные шагами 2 и 3, полагаем равными error.

4. Начальное состояние анализатора строится из множества, содержащего ситуацию [S' ->*S, $].

35. Типы и проверка типов.

Тип данных — фундаментальное понятие теории программирования. Тип данных определяет множество значений, набор операций, которые можно применять к таким значениям и, возможно, способ реализации хранения значений и выполнения операций.

Компилятор должен убедиться, что исходная программа следует как синтаксическим, так и семантическим соглашениями исходного языка. Проверка бывает статической(проверяет компилятор) и динамической(выполняется целевой программой). Компилятор должен сообщать об ошибке, если оператор применяется к несовместимому с ним операнду. Проверка типов может осуществляться сразу в семантическом анализаторе или/и после синтаксического анализа и построения синтак. дерева. Программа проверки типов проверяет, чтобы тип конструкции соответствовал ожидаемому в данном контексте. Информация о типах собирается программой проверки типов, может потребоваться при генерации кода. Построение программы проверки типов базируется на информации о синтаксических конструкциях языка, представлении типов и правилах присвоения типов конструкциям.

Система типов представляет собой набор правил для назначения выражения типов различными частями программы. Программа проверки реализует систему типа синтаксическим способом.(т.е добавлением условий к правилам). Программа проверки типов представляет собой схему трансляции, синтезирующую тип каждого выражения из типов их подвыражений, и может обрабатывать массивы, указатели, инструкции и функции.

Соответствие типов переменных можно сформулировать в виде логических правил типирования.

В системе проверки типов содержатся аксиомы и правила вывода, на основе которых можно выводить типы выражений. Тип выражения определяется из контекста программы.

Например если возьмем выражение Lispa

( let ((x 5) (y 7) (+ x y))

x: int, y: int → (+x y): int (сумма тоже целочисленна)

Информацию, получаемую из контекста, будем называть окружением типирования или просто окружением (Е).

Тот факт, что е имеет тип τ в окружении Е будем записывать: Е├ е : τ. Такое утверждение называется типированием. Если окружение является пустым, например для одной константы 5, то запишем: ├5:Int. В процессе проверки типов окружение может расширяться, т.е. в него могут добавляться новые сведения о типе.

Система проверки типов является дедуктивной системой. В ней аксиомы определяют правильное назначение типа примитивным элементам, а правила – сложным выражениям. А тип сложного выражения определяется исходя из типов составляющих его частей с применением соответствующего правила вывода: t1,t2,…/t, где t1,t2,… - типирование. Если типирование t1,t2,…выполняется (истинно), тогда выполняется и типирование t.

Для суммы двух целых чисел применимо следующее правило типирования:

Е├е1:Int Е├е2:Int

Е├е1+е2:Int

Все выражения программы должны иметь вывод ├е: τ для некоторого типа τ. Такие выражения называются правильно-типированные. Если для какого-то выражения тип вывести нельзя, то транслятор выдаст сообщение о несоответствии типов: type miss match.

31. L–атрибутные грамматики в детерминированном разборе сверху–вниз. а) Устранение левой рекурсии. б) Проектирование детерминированного транслятора.

Определение: Символ в КС-грамматике называется рекурсивным, если для него существует цепочка вывода вида , где .   Определение: Если и , то рекурсия называется левой, а грамматика - леворекурсивной.   Определение: Если и , то рекурсия называется правой, а грамматика - праворекурсивной.   Определение: Если и , то рекурсия представляет собой цикл.   Любая КС-грамматика может быть как леворекурсивной, так и праворекурсивной, а также леворекурсивной и праворекурсивной одновременно.   Некоторые алгоритмы левостороннего разбора для КС-языков не работают с леворекурсивными грамматиками, поэтому возникает необходимость исключить левую рекурсию из правил грамматики.   Любую КС-грамматику можно преобразовать к нелеворекурсивному виду или неправорекурсивному виду.

Устранение левой рекурсии

Пусть задана леворекурсивная схема:

A -> A₁ Y {A.a := g(A₁.a, Y.y)}

A -> X {A.a:=f(X.x)}

Каждый грамматический символ имеет синтрез атрибуты, f g – произвольные функции. Устраняем левую рекурсию:

A -> X R

R -> YR | έ

Получаем

A → X { R.i := f(X.x) }

R { A.a := R.s }

R → Y { R₁.i := g(R.i, Y.y) }

R₁ { R.s := R.i }

R → ε { R.s := R.i }

Трансляция методом рекурсивного спуска

Для построения транслятора мы должны заменить наслед. атрибуты синтезируемыми. Для этого нужно изменить структуру грамматики. Далее мы должны получить набор рекурсивных процедур, которые выполняют трансляцию. Рассмотрим, как эти процедуры построить. Для каждого нетерминала «A» строим ф-цию. В этой ф-ции для каждого наследуемого атрибута добавляем параметр. Ф-ция должна возвращать значения синтезированных атрибутов нетерминала «A». Ф-ции определяют локальные переменные для каждого атрибута, каждого граматического символа, использующего в определении А. Как и предполагает метод рекурсивного спуска ф-ция для нетерминала А сначала разбирает процукцию, которая будет исп-ться в дальнейшем разборе. Для каждой процедуры нужно написать программный код, который будет обрабатывать слева направо последовательность терминалов/нетерминалов, семантических действий, составляющих правую часть продукции:

а) для терминала Х с синтезируемым атрибутом «х» он сохраняет значения атрибутов Х.х. Нужно сопоставить терминал Х с текущим символом входной последовательности. Указатель символа нужно сдвинуть вправо.

б) для нетерминала В нужно сделать вызов С:=В(b1,b2,…,bn).

в) для действия нужно скопировать его код в синтаксический анализатор при этом нужно поменять обращение к атрибутам на обращения к соответствующим переменным

30. L–атрибутные определения. Схемы трансляции. Порядок вычисления семантических правил.

Выделим класс синтаксически управляемых определений L-АО, чьи атрибуты всегда м.б. вычислены, если дерево разбора будет строится в глубину. L-left, т.к. значения атрибутов перемещаются слева направо.

Синтаксическое управление определения называется L-атрибутным, если каждый наследуемый атрибут символа Xi (1<=i<=n) в правой части продукции А→x1, x2,…,xn зависят только:

1)от атрибутов грамматических символов X1, X2,…,Xi-1 (расположенных левее него)

2) от наследуемых атрибутов символа А

А→ X1, X2,…,Xi,…,Xn

Схема трансляции

Схема трансляции – это КСГ, в которой с грамматическими символами связаны атрибуты, а в правых частях продукций между грамматических символов могут встречаться семантические действия, которые обычно заключаются в фигурные скобки.

В схеме трансляции используются как наследуемые, так и синтезируемые атрибуты.

Пример использования СТ, в котором индексные выражения с операциями «+» и «-» переводятся в постфиксные.

9-5+2 → 95-2+

Схема трансляции в постфиксную запись:

E → T R

R → addop T {print (addop.lexem)} R₁ (addop – лекс. класс, включающий в себя знаки «+» и «-»).

T → num {print (num.value)}

П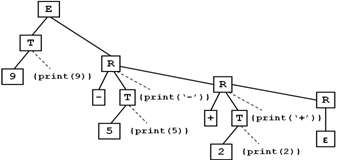 осле построения дерева вставим в него семантические действия: При обходе в глубину получим последовательность операций {print}, печатающих постфиксную запись. Операции {print}включают в дерево как обычные терминалы.

При обходе в глубину выполняются семантические действия и получается постфиксная запись. Семантические действия будут выполняться правильно при использовании L-атрибутных определений.

Практически это используется:

- при использовании только синтезируемых атрибутов необходимо семантические действия расположить в конце правой части соответствующей продукции.

- при использовании еще и наследуемых атрибутов необходимо руководствоваться следующими правилами:

1. наследуемый атрибут грамматического символа правой части продукции д.б. вычислен в действии, стоящем перед этим символом.

2. действие не д. обращаться к синтезируемому атрибуту символа, стоящего от него правее.

3. синтезируемый атрибут нетерминала левой части правила м.б. вычислен только после всех используемых им атрибутов. Такое действие помещается в конце левой части продукции

39. LR-разбор для неоднозначных грамматик.

Любая неоднозначная грамматика не может быть LR-грамматикой, однако ряд типов таких грамматик возможно использовать для определения и реализации языков. Для языков конструкций типа арифметических выражений неоднозначные грамматики обеспечивают более краткую и естественную спецификацию по сравнению с эквивалентными однозначными грамматиками. Также имея неоднозначную грамматику, можно определить специальные конструкции путем добавления в грамматику новых продукций.

При попытке построить таблицу LR-анализа по множеству построенному по неоднозначной грамматике возникают конфликты действий (например если множеству FOLLOW принадлежит несколько терминалов по которым должны произойти разные действия). Эта проблема может быть решена с помощью информации о приоритетах и ассоциативности. В данном случае левоассоциативность (правоассоциативность) рассматривается как превосходство левого (правого) оператора одного и того же вида в случае их последовательного применения (напр: id+id+id).

Если в продукциях неоднозначной грамматике есть нетерминалы(группа нетерминалов), которые могут стоять в конце продукции или отсутствовать (например if then else) то возникший конфликт переноса/свертки решается в пользу переноса этого входного символа (else).

В грамматику можно добавить продукции для определения особого случая синтаксической конструкции. Она порождается общим видом грамматики. Добавив такую продукцию, мы порождаем конфликт, он разрешается согласно правилу свертки по такой особой продукции.

Примером такой особой продукции может случит определение математической формулы Продукцией для неё будет иметь вид E -> E -> E ‘нижний регистр’ E ‘верхний регистр’ E (E- индетификатор). Причиной особой трактовки этой продукции заключается в том что символ ‘i’ относится к нетерминалу, а не к символу k. (входная последовательность будет содержать следующую цепочку: a нижний регистр k верхний регистр i) Это отношение важно в математической записи.