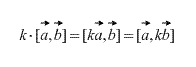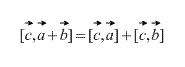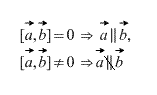Экзамен по математике.
Билет №1.
1.Определители 2 и 3 порядка. Решение систем линейных алгебраических уравнений по формулам Крамера.


Метод Крамера
При небольшой размерности системы m (m = 2,…,5) на практике часто используют формулы Крамера для решения СЛАУ:
 (i
= 1, 2, …, m). Эти формулы позволяют находить
неизвестные в виде дробей, знаменателем
которых является определитель матрицы
системы, а числителем – определители
матриц Ai,
полученных из A заменой столбца
коэффициентов при вычисляемом неизвестном
столбцом свободных членов.
Так А1 получается
из матрицы А заменой первого столбца
на столбец правых частей f.
(i
= 1, 2, …, m). Эти формулы позволяют находить
неизвестные в виде дробей, знаменателем
которых является определитель матрицы
системы, а числителем – определители
матриц Ai,
полученных из A заменой столбца
коэффициентов при вычисляемом неизвестном
столбцом свободных членов.
Так А1 получается
из матрицы А заменой первого столбца
на столбец правых частей f.
Например, для системы двух линейных уравнений

Размерность системы (т.е., число m) является главным фактором, из–за которого формулы Крамера не могут быть использованы для численного решения СЛАУ большого порядка. При непосредственном раскрытии определителей решение системы с m неизвестными требует порядка m!*m арифметических операций. Таким образом, для решения системы, например, из m = 100 уравнений потребуется совершить 10158 вычислительных операций (процесс займёт примерно 1019 лет), что не под силу даже самым мощным современным ЭВМ
2. |
Окружность - определение, уравнение (с выводом)
|
Окружность – замкнутая плоская кривая, все точки которой одинаково удалены от данной точки (центра), лежащей в той же плоскости, что и кривая.
Окружность — геометрическое место точек плоскости, удалённых от некоторой точки — центра окружности — на заданное расстояние, называемое радиусом окружности.
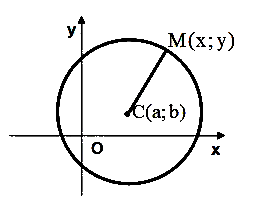
Если
точка С -
центр окружности, R -
ее радиус, а M -
произвольная точка окружности, то из
определения окружности следует, что ![]() .
Последнее равенство есть характеристическое
уравнение окружности радиуса R с
центром в точке C.
.
Последнее равенство есть характеристическое
уравнение окружности радиуса R с
центром в точке C.
Пусть
на плоскости задана прямоугольная
декартова система координат и
точка C(a;b) -
центр окружности радиуса R.Пусть ![]() -
произвольная точка этой окружности.
Как известно, расстояние
-
произвольная точка этой окружности.
Как известно, расстояние ![]() ,
поэтому уравнение можно записать так:
,
поэтому уравнение можно записать так:
![]()
или
![]() -
общее уравнение окружности радиуса R с
центром в точке C.
-
общее уравнение окружности радиуса R с
центром в точке C.
Если центр окружности совпадает с началом координат, то общее уравнение примет вид
![]() Это
уравнение называют каноническим уравнением
окружности.
Это
уравнение называют каноническим уравнением
окружности.
Билет №2.
1. |
Понятие вектора. Виды векторов, линейные операции над векторами. Сложение, вычитание вектора и умножение вектора на скаляр. Вектором называется направленный отрезок, имеющий определенную длину, т. е. отрезок определенной длины, у которого одна из ограничивающих его точек принимается за начало, а вторая — за конец. Сонаправленные и противоположно направленные(лежащие на параллельных прямых)/коллинеарные нулевые, равный, компланарные(3, лежат в одной плоскости) + |
2. |
Эллипс - определение, уравнение(с выводом). Эллипсом называется геометрическое место точек на плоскости, сумма расстоянии которых от двух данных точек этой плоскости есть величина постоянная. Уравнение с выводом - проще
Билет №3. |
1. |
Проекция вектора на ось. Орты. Представление вектора в координатной форме. Линейные операции над векторами в координатной форме. Чтобы проецировать вектор на ось – нужно опустить перпендикуляр на крайние точки вектора. + |
2. |
Гипербола- определение, уравнение(с выводом). Свойства.
|
Билет №4
|
|
1. |
Скалярное произведение двух векторов. Определение и свойства. Представление скалярного произведения при задании векторов в координатной форме. A*b=x*x+y*y+zz если a*b=0 => a перпенд b a*b=1\ то угол >\<90 скалярное произведение нулевых векторов равно 0 тогда и только тогда, когда эти векторы перпендикулярны скалярный квадрат вектора = квадрату его длины а^2>=0, причем a^2>0 при а не равно 0 ab=ba (a+b)c=ac+bc k(ab)=(ka)b
|
2. |
Парабола- определение , уравнение параболы, уравнение директрисы, свойства параболы.
|
Билет №5
1. |
Векторное произведение двух векторов.
|
|
||||||||||||||||||||||
2. |
Понятие пределов функции не определенность возникающая при вычисление некоторых пределов. Виды неопределенностей. Способы раскрытия неопределенностей.
|
|
||||||||||||||||||||||
Билет №6 |
|
|||||||||||||||||||||||
1. |
Смешанное произведение трех векторов. Векторное произведение двух векторов а и b - это операция над ними, определенная лишь в трехмерном пространстве, результатом которой является вектор со следующими свойствами:
Очевидно, что в случае векторного произведения, имеет значение порядок, в котором берутся вектора, более того,
Так же, непосредственно из определения следует, что для любого скалярного множителя k (числа) верно следующее:
Векторное произведение коллинеарных векторов равно нулевому вектору. Более того, векторное произведение двух векторов равно нулю тогда и только тогда, когда они коллинеарны. (В случае, если один из них нулевой вектор необходимо вспомнить, что нулевой вектор коллинеарен любому вектору по определению).
Векторное произведение обладает распределительным свойством, то есть
Выражение векторного произведения через координаты векторов. Пусть даны два вектора
(как найти координаты вектора по координатам его начала и конца - см. статью Скалярное произведение векторов, пункт Альтернативное определение скалярного произведения, или вычисление скалярного произведения двух векторов, заданных своими координатами.) Тогда
Зачем нужно векторное произведение? Существует множество способов применения векторного произведения, например, как уже написано выше, вычислив векторное произведение двух векторов можно выяснить, коллинеарны ли они.
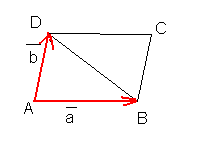
Или же его можно использовать как способ вычисления площади параллелограмма, построенного на этих векторах. Исходя из определения, длина результирующего вектора и есть площадь данного параллелограмма.
Также огромное количество применений существует в электричестве и магнетизме.
|
|
||||||||||||||||||||||
2. |
Понятие производной. Производная, как скорость изменения функции. Геометрическая интерпретация производной.
Билет №7
|
|
||||||||||||||||||||||
1. |
Прямая на плоскости – общее уравнение прямой. Уравнение прямой с угловым коэффициентом. Угол между двумя прямыми. Параллельность и перпендикулярность двух прямых(частные случаи). Прямая на плоскости Общее уравнение прямой. Прежде чем вводить общее уравнение прямой на плоскости введем общее определение линии. Определение. Уравнение вида F(x,y)=0 (1) называется уравнением линии L в заданной системе координат, если этому удовлетворяют координаты х и у любой точки, лежащей на линии L, и не удовлетворяют координаты никакой точки, не лежащей на этой линии. Степень уравнения (1) определяет порядок линии. Будем говорить, что уравнение (1) определяет (задает) линию L. Определение. Уравнение вида Ах+Ву+С=0 (2) при произвольных коэффициентах А, В, С (А и В одновременно не равны нулю) определяют некоторую прямую в прямоугольной системе координат. Данное уравнение называетсяобщим уравнением прямой. Уравнение (2) есть уравнение первой степени, таким образом, каждая прямая есть линия первого порядка и, обратно, каждая линия первого порядка есть прямая. Рассмотрим три частных случая, когда уравнение (2) является неполным, т.е. какой-то из коэффициентов равен нулю. 1) Если С=0, то уравнение имеет вид Ах+Ву=0 и определяет прямую, проходящую через начало координат т.к. координаты (0,0) удовлетворяют данному уравнению. 2) Если В=0 (А≠0), то уравнение имеет вид Ах+С=0 и определяет прямую, параллельную оси ординат. Разрешив это уравнение относительно переменной х получим уравнение вида х=а, где а=-С/А, а— величина отрезка, который отсекает прямая на оси абсцисс. Если а=0 (С=0), то прямая совпадает с осью Оу (рис.1а). Таким образом, прямая х=0определяет ось ординат. 3) Если А=0 (В≠0), то уравнение имеет вид Ву+С=0 и определяет прямую, параллельную оси абсцисс. Разрешив это уравнение относительно переменной у получим уравнение вида у=b, где b=-С/В, b— величина отрезка, который отсекает прямая на оси ординат. Если b=0 (С=0), то прямая совпадает с осью Ох (рис.1б). Таким образом, прямая у=0определяет ось абсцисс.
а) б) Рис.1 Уравнение прямой с угловым коэффициентом. Пусть дано уравнение Ах+Ву+С=0 при условии, что коэффициент В не равен нулю. Выполним следующие преобразования
Уравнение (4), где k=-A/B, называется уравнением прямой с угловым коэффициентом k. Определение. Углом наклона данной прямой к оси Ох назовем угол α, на который нужно повернуть ось Ох, чтобы её положительное направление совпало с одним из направлений прямой. Тангенс угла наклона прямой к оси Ох равен угловому коэффициенту, т.е k=tgα. Докажем, что –А/В действительно равно k. Из прямоугольного треугольника ΔОАВ (рис.3) выразимtgα, выполним необходимые преобразования и получим:
Рис.3 Если k=0, то прямая параллельна оси Ох, и её уравнение имеет вид у=b. Пример. Прямая задана общим уравнением 4х+2у-2=0. Составить для этой прямой уравнение с угловым коэффициентом. Решение. Выполним преобразования, аналогичные описанным выше, получим:
где k=-2, b=1. Угол между двумя прямыми Рассмотрим две прямые l1 и l2:
l1 :
l2 :
φ-
угол между ними (
Рис.4
Отсюда
С
помощью формулы (7) можно определить
один из углов между прямыми. Второй
угол равен Пример. Две прямые заданы уравнениями у=2х+3 и у=-3х+2. найти угол между этими прямыми. Решение. Из уравнений видно, что k1=2, а k2=-3. подставляя данные значения в формулу (7), находим
Условия параллельности и перпендикулярности двух прямых
Если
прямые l1 и l2 параллельны,
то φ=0 и tgφ=0.
из формулы (7) следует, что
Еслипрямые l1 и l2 перпендикулярны,то φ=π/2, α2=π/2+α1 .
|
Прямая на плоскости – общее уравнение прямой. Уравнение прямой с угловым коэффициентом. Угол между двумя прямыми. Параллельность и перпендикулярность двух прямых(частные случаи).
|
||||||||||||||||||||||
2. |
Правило дифференцирования суммы произведения и частного двух функций. Таблица производных основных элементарных функций.
|
Правило дифференцирования суммы произведения и частного двух функций. Таблица производных основных элементарных функций.
|
||||||||||||||||||||||
|
|
|
||||||||||||||||||||||
Билет №8 |
|
|||||||||||||||||||||||
1. |
Прямая на плоскости. Уравнение прямой проходящей через две заданные точки. Расстояние от точки до прямой.
Уравнение прямой, проходящей через две данные точки. Пусть даны две точки М1(х1,у1) и М2(х2,у2). Запишем уравнение прямой в виде (5), где k пока неизвестный коэффициент:
Так
как точка М2 принадлежит
заданной прямой, то её координаты
удовлетворяют уравнению (5):
Если
Пример. Записать уравнение прямой, проходящей через точки М1(1,2) и М2(-2,3)
Решение.
Длинна перпендикуляра опущенного из этой точки на прямую уравнение D=|Ax0+B1y+C1|\sqrt((A^2)+(B^2)) где (Х0;У0) – координаты точки М прямая Ax+By+C=0
|
|
||||||||||||||||||||||
2. |
Max и min функции. Интервалы возрастания и убывания функции применение производных для нахождения точек экстремума и для нахождения интервалов возрастания и убывания функций. Билет №9 |
|
||||||||||||||||||||||
1. |
Окружность- определение, уравнение (с выводом)
|
|
||||||||||||||||||||||
2. |
Асимптоты графика функции- определение, нахождение уравнений, частные случаи. Асимптота – это прямая, к которой график функции приближается, но не пересекает ее y=kx+b k=lim(x-беск) (f(x))\x , если к – число, то находим b=lim(x-беск) (f(x)-kx) под асимптотой подразумевается такая линия, которая, будучи неопределенно продолжена, приближается к данной кривой линии или к некоторой ее части так, что расстояние между обеими линиями делается менее всякой данной величины; если к=0 -> то y=b прямая параллельно оси х – горизонтальная асимптота х=к – вертикальная асимптота
|
|
||||||||||||||||||||||
Билет№10 |
|
|||||||||||||||||||||||
1. |
Эллипс - определение, уравнение(с выводом).
|
|
||||||||||||||||||||||
2. |
Полное исследование функции и построение графика. 1ооф 2производную и стационарные точки 3промежутки возрастания и убываения 4точки экстремума(макс и мин) и значение функции в этих точках и точки перегиба производная =0, но вторая производная меняет знак с плюса на минус или с минуса на + 5 ассимптоты 6построение графика http://www.lawrencenko.ru/files/calc1-l11-lawrencenko.pdf |
|
||||||||||||||||||||||