9.Импульсная переходная функция и переходная характеристика цепи, их связь между собой и с другими схемными функциями.

Импульсная переходная характеристика представляет собой реакцию схемы на входное воздействие в виде δ-функции.

w(t) импульсная переходная характеристика

w(t) = u_вых(t) при u_вх(t) = δ(t)

Импульсная функция – δ(t) функция (с А_m->∞,S->1,t_и = 0)

δ(t) = p·1/p = 1

w(p) = K_U(p)

w(t) = Z^-1{K_U(p)}, где Z^-1 – обратное преобразование Лапласа.

w(t) = Ф^-1{K_U(jω)}.

Изображением w(t) является передаточная функция K_U(p).

Непосредственно временную характеристику y(t) можно найти через переходную и импульсную характеристики.

10.Сопротивление, ёмкость и индуктивность в цепи синусоидального тока

1 ) Резистивный элемент в цепи синусоидального тока.

_,

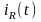
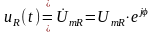
Выводы: фазы тока и напряжения совпадают, мощность в цепи синусоидального тока, выделяющиеся на сопротивлении, имеющем постоянную и переменную составляющую и всегда больше нуля, то есть резистор всегда потребляет энергию от источников переменного тока, поэтому он является активным сопротивлением.

В комплексной форме:

Л ишь значение тока имеет своим изображением на комплексной плоскости комплексную амплитуду:

(закон Ома)

2) Индуктивный элемент в цепи синусоидального тока.

_,

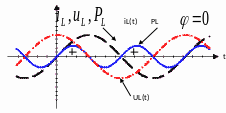
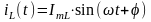
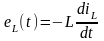
e_L(t) – ЭДС самоиндукции

L – коэффициент между током и потоком

Таким образом, токи и напряжения находятся в квадратуре.

Мгновенная мощность:

Поскольку мощность меняется по гармоническому закону и в одну четвёртую периода мощность запасает энергию, а в следующую часть отдаёт, т.е. не потребляет энергию от источника, то в целом за период синусоидального тока индуктивность не потребляет энергию от источника гармонических колебаний и является поэтому реактивным элементом и обладает реактивным сопротивлением.

- реактивное сопротивление.

В цепи постоянного тока Х_L = 0 (ω = 0) и индуктивность – короткозамкнутый элемент.

Из временной диаграммы следует, что напряжение на индуктивности опережает ток на угол .

В комплексной форме:

, - комплексное сопротивление индуктивности.

₍

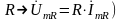
- Закон Ома.

Выводы: 1) Умножение на j учитывает поворот вектора на угол (Напряжение опережает ток на угол ). Закон Ома в этом случае для элемента цепи записывается с учётом комплексного сопротивления: .

2) Поскольку для резистивного элемента (активного сопротивления) мгновенная мощность положительна, то резистивный элемент в цепи синусоидального тока имеет активную мощность.

3) Поскольку для индуктивного элемента мгновенная мощность в течение периода меняется, а само сопротивление индуктивного элемента реактивное, то и мощность индуктивного элемента реактивная.

Амплитуда колебаний мгновенной мощности называется реактивной мощностью:

3) Ёмкостной элемент в цепи синусоидального тока.

_,

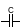
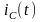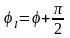
- реактивная проводимость.

Из приведённых соотношений следует, что ток ёмкости опережает напряжение на π/2.

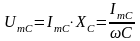
- реактивное сопротивление.

Амплитуда колебаний мгновенной мощности в емкости: - реактивная мощность.

М ощность в ёмкостном элементе ¼ периода положительна (потребляет энергию), а другую часть периода отрицательна (отдаёт энергию). В целом ёмкостной элемент не потребляет энергию, поэтому ёмкость – реактивный элемент и имеет реактивное сопротивление – X_C. Кроме того, амплитуда колебаний мгновенной мощности определяет реактивную мощность ёмкости.

В комплексной форме получаем:

- Закон Ома.

В ывод: Из приведённых выражений для индуктивного и ёмкостного элемента следует, что умножение на +j определяет поворот на угол π/2, а умножение на –j – поворот на - π/2, т.е. напряжение на ёмкости отстаёт от тока на π/2.

Векторная диаграмма:

В данном случае векторная диаграмма упрощает решение интегро-дифференциального уравнения цепи.