Билет 8. Энергия электростатического поля. Энергия заряженного конденсатора. Энергия диполя во внешнем поле.

Энергия электростатического поля - это энергия системы неподвижных точечных зарядов, энергия уединенного заряженного проводника и энергия заряженного конденсатора.

Если имеется система двух заряженных проводников (конденсатор), то полная энергия системы равна сумме собственных потенциальных энергий проводников и энергии их взаимодействия.

Энергия взаимодействия дискретных зарядов. Допустим, что имеются заряженные шары очень маленького диаметра, который меньше расстояния между центрами шаров. Распределение заряда в шарах сферически симметрично. Величина (1) равна работе, которая совершается при разведении зарядом q1 и q2 от расстояния r между ними до бесконечности. Эта работа положительна, когда заряды одноимённы и между ними действуют силы отталкивания. Между разноимёнными зарядами действуют силы притяжения и работа отрицательна. В последнем случае необходимо совершить работу за счёт внешних источников энергии. Поэтому в соответствии с общим определением (1) есть энергия взаимодействия заряженных шаров. Поскольку оба заряда входят в формулу (1) симметрично, её целесообразно записать в виде:

где потенциал созданный 2 зарядом в центре первого; (см. предыд.). Несколько шаров: Энергия взаимодействия при непрерывном распределении зарядов. - потенциал в точке элемента dV.

Рассчитаем энергию заряженного конденсатора. Конденсатор состоит из двух, первоначально незаряженных, пластин. Будем постепенно отнимать у нижней пластины заряд dq и переносить его на верхнюю пластину (рис. 5.15).

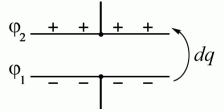
В результате между пластинами возникнет разность потенциалов   При переносе каждой порции заряда совершается элементарная работа.

      Воспользовавшись определением емкости   получаем ;

      Общая работа, затраченная на увеличение заряда пластин конденсатора от 0 до q, равна:

;

При вычислении интеграла учтено, что емкость С не зависит от q и φ. Величина полной работы А равна энергии, запасенной конденсатором:

Эту энергию можно также записать в виде

Запасание энергии конденсатором наглядно проявляется при его подключении к электрической лампочке. Лампочка вспыхивает и гаснет при разрядке конденсатор.

Энергия диполя во внешнем поле. Эта энергия равна сумме энергий зарядов диполя. ; Разложим в ряд по I. где в следствие чрезвычайной малости сохранены лишь члены первого порядка по . Формула принимает вид ;

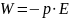Билет 9. Постоянное электрическое поле при наличии диэлектрика. Поляризованность диэлектрика. Диэлектрическая восприимчивость и диэлектрическая проницательность.

Влияние вещества на электрическое и магнитное поля было открыто и исследовано Фарадеем. Результаты этих работ привели Фарадея к идее близкодействия и концепции электрического поля. Электростатическая индукция была им открыта в 1837г. Тогда же он ввел в науку термины «диэлектрик» и «диэлектрическая постоянная».

Пусть в некотором объеме V имеется непрерывно распределенный заряд с объемной плотностью , но пусть в целом объем электрически нейтральный, тогда 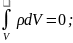 (11.1)

Если  =0 во всех точках объема, то эта система электрически нейтральна, а именно на нее не действует внешнее поле и сама она не способна создавать поле. Если же  в одних частях объема положительна, а в других отрицательна, то хотя в целом заряд объема равен нулю, такая система способна создавать электрическое поле и на нее действует внешняя электрическая сила. В первом приближении электрические свойства нейтральной системы характеризуются ее дипольным моментом. Если взять два точечных заряда q и (-q) и расположить их на расстоянии l, то такая с истема будет обладать дипольным моментом (см.(7.7))  .

При непрерывном распределении заряда по объему V дипольный момент (11.2)

Где радиус-вектор отсчитывается от точки O, принятой за начало отсчета.

Величина (11.2) не зависит от того, какая точка выбрана за начало системы отсчета. Если за начало отсчета выбрать точку  , положение которой относительно точки О характеризуется радиус-вектором  , то дипольный момент непрерывного распределения зарядов относительно этой точки будет равен  (11.3)

Е сли взять два сколь угодно малых элементарных объема  И  С зарядами  И  , то дипольный момент

, (11.4)

Г де   и   - радиус-векторы этих объемов. Если, например, в объеме   находится положительный заряд  =Q. Тогда вследствие электрической нейтральности системы  =-Q И формула (11.4) принимает вид:

, что совпадает с (7.7).