Закон прямолинейного распространения света.

Свет в однородной среде распространяется прямолинейно.

Луч – часть прямой, указывающей направление распространения света. Понятие луча ввел Евклид (геометрическая или лучевая оптика – раздел оптики, изучающий законы распространения света, основанные на понятии луча, без учета природы света).

Прямолинейностью распространения света объясняется образование тени и полутени.

При малых размерах источника (источник, находится на расстоянии, по сравнению с которым размерами источника можно пренебречь) получается только тень (область пространства, в которую свет не попадает).

При больших размерах источника света (или, если источник находится близко к предмету) создаются нерезкие тени (тень и полутень).

В астрономии – объяснение затмений.

Световые пучки распространяются независимо друг от друга. Например, проходя один через другой, они не влияют на взаимное распространение.

Световые пучки обратимы, т.е., если поменять местами источник света и изображение, полученное с помощью оптической системы, то ход лучей от этого не изменится.

Закон независимости световых лучей утверждает, что лучи при пересечении не возмущают друг друга. При больших интенсивностях этот закон не соблюдается, происходит рассеяние света на свете.

Когерентными наз. процессы нелинейного взаимодействия световых волн, существенно зависящие от фазовых соотношении. Соответственно, к некогерентным относятся нелинейные оптич. процессы, зависящие лишь от интенсивностей волн. Понятия когерентности и нскогерентности в нелинейной оптике играют важную роль, в первую очередь при классификации многоволновых взаимодействий (многофотонных процессов) и резонансных эффектов.

Многоволновые взаимодействия наз. когерентными, если они происходят без передачи энергии среде. В этом случае фазовое согласование отдельных компонент поля возникает в результате одновременного выполнения законов сохранения энергии и импульса только для волн, без участия среды. Такие процессы наз. также параметрическими.

При взаимодействии световых полей в условиях одно- или многофотонных резонансов с квантовыми переходами в среде когерентными наз. нестационарные процессы, за время развития к-рых фазовые соотношения между полем и откликом вещества не успевают существенно нарушиться релаксацией (см. Оптическая нутация, Самоиндуцированная прозрачность. Фотонное эхо). В противоположном случае процессы становятся некогерентными.

Представления о когерентности процессов используются также при анализе распространения волн в нелинейных средах, когда необходимо учитывать пространственную эволюцию фазовых соотношений. В этом случае процесс может быть когерентен локально, а при распространении в среде может произойти полная или частичная потеря когерентности. Подобная ситуация реализуется, напр., при параметрическом взаимодействии случайно модулированных волн в диспергирующих средах.

Интерференция - явление взаимодействия в пространстве нескольких (двух или более) когерентных волн, при котором имеется усиление или ослабление результирующей волны в зависимости от того, в какой фазе волна оказывается в данной точке пространства.

Интерферировать могут лишь когерентные волны. Максимумы наблюдаются при разности хода, равной длине волны. Очевидно, что воздействия бионов приходящие от разных щелей взаимно усиливают друг друга. Минимумы наблюдаются при разности хода равной нечётному количеству полуволн и колебания от разных щелей взаимно уничтожают друг друга.

Интерференция света - пространственное перераспределение светового потока при взаимодействии двух (или нескольких) когерентных волн, в результате которого в разных местах возникают минимумы и максимумы его интенсивности.

Принцип интерференции был открыт в 1802 году, когда англичанин Т. Юнг, врач по профессии, человек с очень разносторонними интересами, провёл ставший теперь классическим "опыт с двумя отверстиями". В экране кончиком булавки прокалывались две близко расположенные дырочки, которые освещались солнечным светом из небольшого отверстия в зашторенном окне. За экраном Юнг наблюдал вместо двух ярких точек серию чередующихся темных и светлых колец.

На границе раздела двух сред падающий световой поток делится на две части: одна часть отражается, другая – преломляется.

В. Снелл (Снеллиус) до X. Гюйгенса и И. Ньютона в 1621 г. экспериментально открыл закон преломления света, однако не получил формулу, а выразил его в виде таблиц, т.к. к этому времени в математике еще не были известны функции sin и cos.

Преломление света подчиняется закону:

1.Луч падающий и луч преломленный лежат в одной плоскости с перпендикуляром, восставленным в точке падения луча к поверхности раздела двух сред.

2.Отношение синуса угла падения к синусу угла преломления для двух данных сред есть величина постоянная (для монохроматического света).

Причиной преломления является различие скоростей распространения волн в различных средах.

Величина, равная отношению скорости света в вакууме к скорости света в данной среде, называется абсолютным показателем преломления среды. Это табличная величина – характеристика данной среды.

Величина, равная отношению скорости света в одной среде к скорости света в другой, называется относительным показателем преломления второй среды относительно первой.

Доказательство закона преломления.

Распространение падающих и преломленных лучей: ММ' — граница раздела двух сред. Лучи А1А и В1В — падающие лучи; α — угол падения;. АС – волновая поверхность в момент, когда луч А1А достигнет границы раздела сред. Воспользовавшись принципом Гюйгенса построим волновую поверхность в тот момент, когда луч В1В достигнет границы раздела сред. Построим преломленные лучи АА2 и ВВ2. β — угол преломления. АВ – общая сторона треугольников АВС и АВD. Т.к. лучи и волновые поверхности взаимно перпендикулярны, то угол ABD= α и угол BAC=β. Тогда получим:

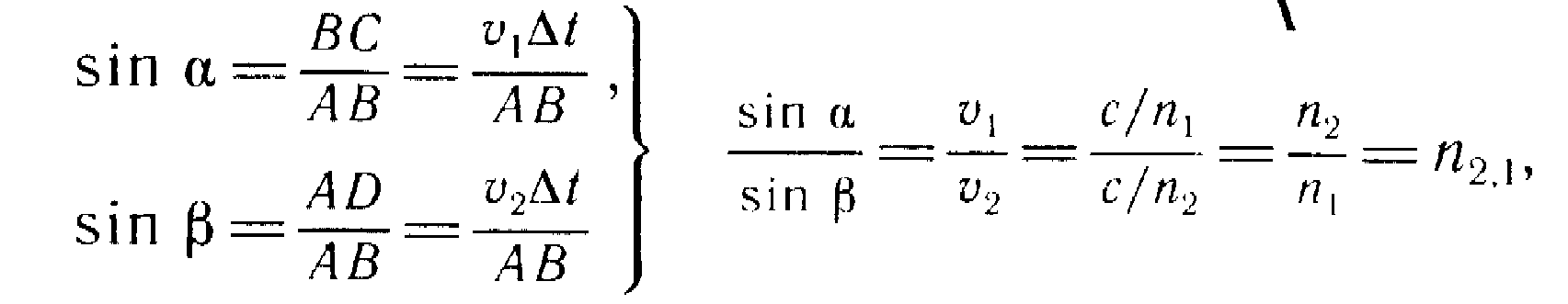
В призме или плоскопараллельной пластине преломление происходит на каждой грани в соответствие с законом преломления света. (Внимание! Не забудьте, что всегда существует отражение. Кроме того, реальный ход лучей зависит и от показателя преломления, и от преломляющего угла – угла при вершине призмы.)

Принцип Ферма

Принцип Ферма (принцип наименьшего времени Ферма) в геометрической оптике — постулат, предписывающий лучу света двигаться из начальной точки в конечную точку по пути, минимизирующему (реже - максимизирующему) время движения (или, что то же самое, минимизирующему оптическую длину пути ).

Этот принцип, сформулированный в I в. Героном Александрийским для отражения света, в общем виде был сформулирован Пьером Ферма около 1660 года в качестве самого общего закона геометрической оптики. В разнообразных конкретных случаях из него следовали уже известные законы: прямолинейность луча света в однородной среде, законы отражения и преломления света на границе двух прозрачных сред.

Законы геометрической оптики и принцип Ферма

Конечность и постоянство скорости света позволяет вывести из принципа Ферма все три закона геометрической оптики.

Закон прямолинейного распространения

Поскольку свет распространяется в однородной среде с постоянной скоростью, то минимальность времени становится эквивалентной минимальному расстоянию. Поэтому доказательство закона прямолинейного распространения света из принципа Ферма тривиально: Свет в однородной среде движется по кратчайшему расстоянию, соединяющему две точки, т.е. по отрезку прямой.

Закон отражения

Для доказательства закона отражения света можно обратиться к рисунку. Если отразить точечный источник S в зеркале, то для любой точки R' будет верно равенство длин отрезков: SR' = S'R' . Поэтому время прохождения света по пути S → R' → А будет равно времени прохождения света по пути S' → R' → А . Согласно принципу Ферма свет будет распространяться по «кратчайшему расстоянию», а из всех подобных расстояний минимальное будет для пути S' → R → А , когда точка R' будет находиться на отрезке S'А , соединяющем мнимое изображение источника и точку наблюдения (глаз). Не трудно видеть, что для этой точки угол падения равен углу отражения.

Это доказательство, естественно, не является строгим. По старой доброй традиции вставлю фразу: «Пытливый читатель может провести строгое доказательство самостоятельно». Перечислю лишь теоремы планиметрии, которые в нем использовались:

Признак равенства прямоугольных треугольников;

Неравенство треугольника;

Теорема о равенстве вертикальных углов;

На самом деле, в законе отражения есть еще фраза, которую многие часто забывают: падающий и отраженный лучи должны лежать в одной плоскости. Таким образом полное доказательство закона отражения не возможно без привлечения стереометрии. Эту часть доказательства «пытливый читатель также может провести строгое доказательство самостоятельно»