11.3. Логарифмы

Термин «логарифм» возник из сочетания греческих слов logos — отношение, соотношение и arithmos — число.

Основные свойства логарифма позволяют заменить умножение, деление, возведение в степень и извлечение корня более простыми действиями сложения, вычитания, умножения и деления.

Логарифмом обозначается обычно loga N. Логарифм с основанием е = 2,718... называется натуральным и обозначается ln N. Логарифм с основанием 10 называется десятичным и обозначается lg N. Равенство у = loga x определяет логарифмическую функцию.

«Логарифм данного числа N при основании а, показатель степени у, в которую нужно возвести число а, чтобы получить N; таким образом,

N = a y».

Изобретателем логарифмов был Непер (Нейпир) (Napier) Джон (1550-1617), шотландский математик.

Потомок старинного воинственного шотландского рода. Изучал логику, теологию, право, физику, математику, этику. Увлекался алхимией и астрологией. Изобрел несколько полезных сельскохозяйственных орудий. В 1590-х годах пришел к идее логарифмических вычислений и составил первые таблицы логарифмов, однако свой знаменитый труд «Описание удивительных таблиц логарифмов» опубликовал лишь в 1614. В конце 1620-х годов была изобретена логарифмическая линейка, счетный инструмент, использующий таблицы Непера для упрощения вычислений. С помощью логарифмической линейки операции над числами заменяются операциями над логарифмами этих чисел.

В 1617, незадолго до своей смерти, Непер изобрел математический набор для облегчения арифметических вычислений. Набор состоял из брусков с нанесенными на них цифрами от 0 до 9 и кратными им числами. Для умножения какого-либо числа бруски располагали рядом так, чтобы цифры на торцах составляли это число. Ответ можно было увидеть на боковых сторонах брусков. Помимо умножения, палочки Непера позволяли выполнять деление и извлечение квадратного корня.

11.4. Суммирующая машина Блеза Паскаля

В 1640 г. попытку создать механическую вычислительную машину предпринял Блез Паскаль (1623—1662).

Существует мнение, что «на идею счетной машины Блеза Паскаля натолкнуло, по всей вероятности, учение Декарта, который утверждал, что мозгу животных, в том числе и человека, присущ автоматизм, поэтому ряд умственных процессов ничем по существу своему не отличается от механических». Косвенным подтверждением этого мнения служит то, что Паскаль поставил перед собой цель создать такую машину. В 18 лет он начинает работать над созданием машины, с помощью которой даже незнакомый с правилами арифметики мог производить различные действия.

Первая работающая модель машины была готова уже в 1642 году. Паскаля она не удовлетворила, и он сразу же начал конструировать новую модель. «Я не экономил,— писал он впоследствии, обращаясь к «другу-читателю»,— ни времени, ни труда, ни средств, чтобы довести ее до состояния быть тебе полезной... Я имел терпение сделать до 50 различных моделей: одни деревянные, другие из слоновой кости, из эбенового дерева, из меди...»

Паскаль экспериментировал не только с материалом, но и с формой деталей машины: модели были сделаны — «одни из прямых стержней или пластинок, другие из кривых, иные с помощью цепей; одни с концентрическими зубчатыми колесами, другие с эксцентриками; одни — движущиеся по прямой линии, другие— круговым образом; одни в форме конусов, другие — в форме цилиндров...»

Наконец в 1645 году арифметическая машина, как назвал ее Паскаль, или Паскалево колесо, как называли ее те, кто был знаком с изобретением молодого ученого, была готова.

Она представляла собой легкий латунный ящичек размером 350X25X75 мм (Рисунок 11 .76). На верхней крышке — 8 круглых отверстий, вокруг каждого нанесена круговая шкала.

Рисунок 11.76 - Машина Паскаля со снятой крышкой

Шкала крайнего правого отверстия разделена на 12 равных частей, шкала соседнего с ним отверстия — на 20 частей, шкалы остальных 6 отверстий имеют десятичное деление. Такая градуировка соответствует делению ливра—основной денежной единицы того времени — на более мелкие: 1 су = 1/20 ливра и 1 денье — 1/12 су.

В отверстиях видны зубчатые колеса, находящиеся ниже плоскости верхней крышки. Число зубьев каждого колеса равно числу делений шкалы соответствующего отверстия (например, у крайнего правого колеса 12 зубьев). Каждое колесо может вращаться независимо от другого на собственной оси. Поворот колеса осуществляется от руки с помощью ведущего штифта, который вставляется между двумя смежными зубьями. Штифт поворачивает колесо до тех пор, пока не наталкивается на неподвижный упор, закрепленный в нижней части крышки и выступающий внутрь отверстия левее цифры 1 круговой шкалы. Если, например, вставить штифт между зубьями, расположенными против цифр 3 и 4, и повернуть колесо до упора, то оно повернется на 3/10 полного поворота.

Поворот колеса передается посредством внутреннего механизма машины цилиндрическому барабану, ось которого расположена горизонтально. На боковой поверхности барабана нанесены два ряда цифр; цифры нижнего ряда расположены в порядке возрастания— 0, ..., 9, цифры верхнего ряда — в порядке убывания—9, 8, ..., 1,0. Они видны в прямоугольных окнах крышки. Планка, которая помещается на крышке машины, может передвигаться вверх или вниз вдоль окон, открывая либо верхний, либо нижний ряд чисел в зависимости от того, какое математическое действие нужно произвести.

В отличие от известных счетных инструментов типа абака в арифметической машине вместо предметного представления чисел использовалось их представление в виде углового положения оси (вала) или колеса, которое несет эта ось. Для выполнения арифметических операций Паскаль заменил поступательное перемещение камешков, жетонов и т. д. в абаковидных инструментах на вращательное движение оси (колеса), так что в его машине сложению чисел соответствует сложение пропорциональных им углов.

Колесо, с помощью которого осуществляется ввод чисел (так называемое установочное колесо), в принципе не обязательно должно быть зубчатым — этим колесом может быть, например, плоский диск, по периферии которого через 36° просверлены отверстия, в которые вставляется ведущий штифт.

Нам осталось познакомиться с тем, как Паскаль решил самый, пожалуй, трудный вопрос,— о механизме переноса десятков. Наличие такого механизма, позволяющего вычислителю не тратить внимания на запоминание переноса из младшего разряда в старший,— это наиболее разительное отличие машины Паскаля от известных счетных инструментов.

На Рисунок 11 .77 изображены элементы машины, относящиеся к одному разряду: установочное колесо N, цифровой барабан I, счетчик, состоящий из 4 корончатых колес В, одного зубчатого колеса К и механизма передачи десятков. Заметим, что колеса В1 В4 и К не имеют принципиального значения для работы машины и используются лишь для передачи движения установочного колеса N цифровому барабану I. Зато колеса В2 и В3 — неотъемлемые элементы счетчика и в соответствии со «счетно-машинной» терминологией именуются счетными колесами. На показаны счетные колеса двух соседних разрядов, жестко насаженные на оси А₁ и A₂, и механизм передачи десятков, который Паскаль назвал «перевязь» (sautoir). Этот механизм имеет следующее устройство.

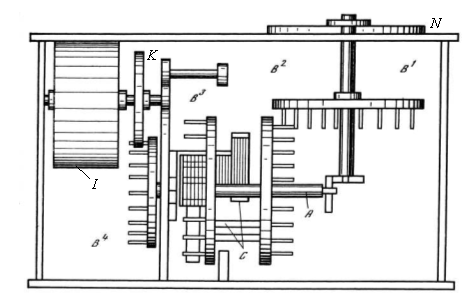
Рисунок 11.77 - Элементы машины Паскаля, относящиеся к одному разряду числа

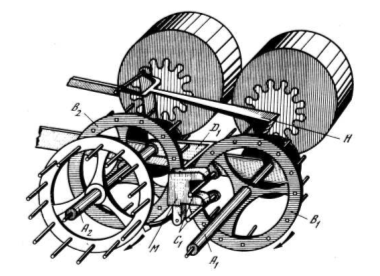
Рисунок 11.78 - Механизм передачи десятков в машине Паскаля

На счетном колесе В₁ младшего разряда имеются стержни d, которые при вращении оси A₁ входят в зацепление с зубьями вилки М, расположенной на конце двухколенного рычага D₁. Этот рычаг свободно вращается на оси А₂ старшего разряда, вилка же несет на себе подпружиненную собачку. Когда при вращении оси А₁ колесо В₁ достигнет позиции, соответствующей цифре б, стержни С1 войдут в зацепление с зубьями вилки, а в тот момент, когда оно перейдет от 9 к 0, вилка выскользнет из зацепления и под действием собственного веса упадет вниз, увлекая за собой собачку. Собачка и протолкнет счетное колесо В₂ старшего разряда на один шаг вперед (то есть повернет его вместе с осью A₂ на 36°). Рычаг Н, оканчивающийся зубом в виде топорика, играет роль защелки, препятствующей вращению колеса В₁ в обратную сторону при поднимании вилки.

Механизм переноса действует только при одном направлении вращения счетных колес и не допускает выполнения операции вычитания вращением колес в обратную сторону. Поэтому Паскаль заменил эту операцию операцией сложения с десятичным дополнением.

Пусть, например, необходимо из 532 вычесть 87. Метод дополнения приводит к действиям:

532 — 87 = 532 — (100—13) = (532 + 13) — 100 = 445.

Нужно только не забыть вычесть 100. Но на машине, имеющей определенное число разрядов, об этом можно не заботиться. Действительно, пусть на 6-разрядной машине выполняется вычитание: 532 — 87. Тогда 000532 + 999913 = 1000445. Но самая левая единица потеряется сама собой, так как переносу из 6-го разряда некуда, деться. В машине Паскаля десятичные дополнения написаны в верхнем ряду цифрового барабана. Для выполнения операции вычитания достаточно передвинуть планку, закрывающую прямоугольные окна, в нижнее положение, сохранив при этом направление вращения установочных колес.

С изобретения Паскаля начинается отсчет времени развития вычислительной техники. В XVII—XVIII вв. один изобретатель за другим предлагают новые варианты конструкций суммирующих устройств и арифмометров, пока, наконец, в XIX в. неуклонно растущий объем вычислительных работ не создал устойчивого спроса на механические счетные устройства и не позволил наладить их серийный выпуск.