6.4.5Числовой метод контроля

При числовом методе контроля код заданного числа определяется как наименьший положительный остаток от деления числа на выбранный модуль р:

r_A = A-{A/p}p

где в фигурных скобках {} — целая часть от деления числа; А — контролируемое число.

Величина модуля р существенно влияет на качество контроля; если р = q (q — основание системы счисления, в которой выражено число) и имеет место числовой контроль, то контролируется только младший разряд числа и контроль как таковой не имеет смысла; для р = q^m справедливы аналогичные соображения, так как если m<n, то опять не все разряды числа участвуют в контроле и ошибки в разрядах старше m вообще не воспринимаются.

При числовом методе контроля по модулю p для определения остатка используют операцию деления, требующую больших затрат машинного времени. Для числового метода контроля справедливы основные свойства сравнений (сложение, умножение сравнений и т. д.). Поэтому, если А ≡ r_А(mod p);

В = rB(mod p), где 0≤rA≤p-1; 0≤rB≤p-1, то А + В = r_а + rB (mod p). Отсюда

r_A+B≡rA + rB(mod p)

Аналогичным образом доказывается справедливость и следующих соотношений:

r_A-B≡rA - rB(mod p);

r_AB≡rArB(mod p).

6.4.6Цифровой метод контроля

При цифровом методе контроля контрольный код числа образуется делением суммы цифр числа на выбранный модуль:

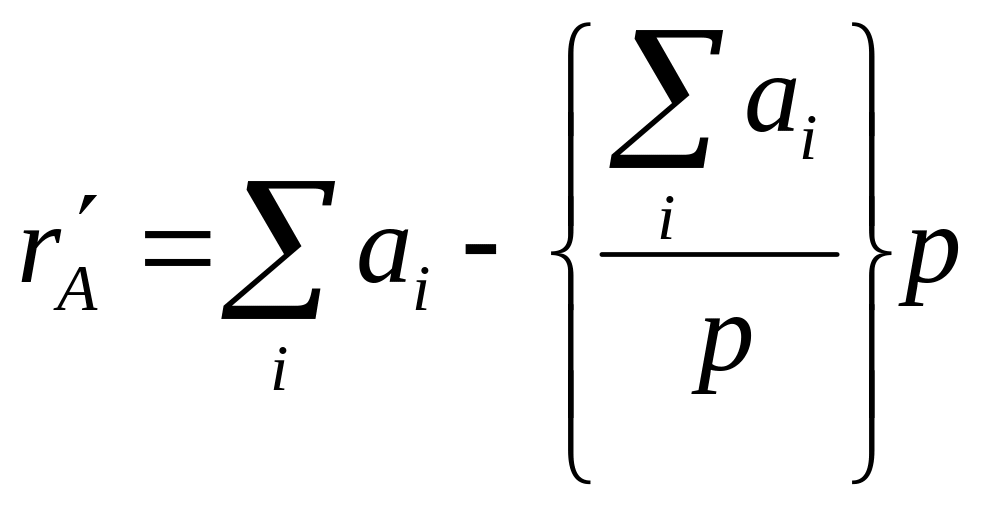
или

Возможны два пути получения контрольного кода: 1)непосредственное деление суммы цифр на модуль р; 2) суммирование цифр по модулю р.

Второй путь проще реализуется, так как если аi < р , то контрольный код получается только операцией суммирования.

Однако при цифровом методе свойства сравнений не всегда справедливы, и происходит это из-за наличия переносов (заемов) при выполнении арифметических действий над числами. Поэтому нахождение контрольного кода результата операции происходит обязательно с коррекцией.

Пусть заданы числа А и В и соответственно их контрольные коды

; ; C = A + B.

Найдем контрольный код

Видимо, когда есть результат операции, тогда найти методом суммирования цифр по модулю не сложно. Какова будет возможность получения через контрольные коды слагаемых ?

Сумму цифр ci числа можно найти, зная цифры ai и bi и количество переносов в каждом разряде. Каждый перенос уносит из данного разряда q единиц и добавляет одну единицу в следующий разряд, т. е. сумма цифр уменьшится на величину q-1 на каждый перенос. Тогда

,

где l — количество переносов, возникших при сложении.

Так как ; , то .

Подставив эти значения в предыдущую формулу, получим

.

Аналогичными рассуждениями можно показать, что для разности чисел

С = А - В

где s - количество заемов при выполнении операции.

6.4.7Выбор модуля для контроля

Достоинства числового метода контроля — в справедливости свойств сравнений для контрольных кодов, что облегчает контроль арифметических операций; достоинства цифрового метода в возможности достаточно просто получать контрольные коды без значительных затрат времени. Чтобы сохранить эти достоинства, необходимо выполнение условия r_A = r’_A.

Так как r_а ≡ А(mod р); r'_А ≡ ∑аi(mod p), имеем аiqi ≡ ∑аi(mod p),

Это равенство возможно тогда, когда почленно обе части выражения равны: аiqi ≡ аi(mod p), или qi ≡ l(mod p),

Последнее выражение можно получить, если в сравнении q ≡ 1(mod p) возводить обе части в одну и ту же степень. Следовательно, p = 1(mod р), или

q = mp+1,

где т — целое число.

Из предыдущего следует, что

p = (q-1)/т.

В результате получено, что для сохранения условия r_A = r'_А необходимо наложить ограничения на модуль р.

Анализ показывает, что для двоичной системы счисления нет целочисленного решения. Это значит, что контролируемую информацию надо представлять в некоторой промежуточной системе счисления. Выбор промежуточной системы счисления определяется величиной модуля р.

К модулю р предъявляют следующие общие требования:

1. величина модуля р должна быть такой, чтобы возникновение любой арифметической или логической ошибки нарушало сравнимость контроль­ных кодов;

2. образование контрольного кода должно осуществляться по возможности простыми средствами;

3. величина модуля р должна быть по возможности небольшой, так как необходимость выполнения контрольных операций ведет к увеличению вспомогательного оборудования.

Ввиду того, что цифровая информация в ЭВМ должна представляться символами двоичного алфавита, для контроля целесообразно перейти к системам счисления с основанием q=2^S, где s — некоторое целое положительное число (s ≥ 2). Переход от двоичного представления исходной информации к новому представлению с основанием q=2^S осуществляется разбиением информации на группы по S разрядов с последующим суммированием этих групп по модулю р = (2S-1)/т или при т = 1, р = 2S - 1.

В самом деле, если s = 2 , то исходная информация разбивается на диады, при s = 3 — на триады, при s = 4 — на тетрады и т. д.

Свертывание — процесс разбиения кодовой комбинации на группы и получения контрольного кода. Как правило, свертки (свернутые коды) образуются в результате суммирования выделенных групп (диад, триад и т. п.) по модулю р. В теории кодирования показано, что модуль можно выбирать из условия

р = (2^S±1)/т.

Рассмотрим частные случаи образования сверток при наиболее распространенных значениях модуля р.

1. Контроль по модулю 3 (m = 1,s = 2, p = 3). Здесь контролируемая информация представляется символами четверичной системы, и свертки образуются суммированием диад по модулю 3. Так как 22 = 1(mod 3), потребуется двухразрядный двоичный сумматор с цепью циклического переноса из старшего разряда в младший.

2. Контроль по модулю 7 (т = 1, s = 3, р = 7) . Здесь контролируемая информация разбивается на триады и представляется символами восьмеричной системы. Так как 23 = 1(mod 7), для получения свертки нужно иметь трехразрядный двоичный сумматор с цепью циклического переноса.

3. Контроль по модулю 5 (т = 1, s = 2, р = 5). Из теории чисел известно, что для того, чтобы число, выраженное в системе с основанием q, делилось на число q + 1, необходимо и достаточно, чтобы разность между суммой цифр, стоящих на четных и нечетных местах, или наоборот, делилась на величину q+1 без остатка.

Из этого правила можно сделать следующий вывод: контрольный код по mod(q + 1) определяется по формуле

где b_i, — двоичное изображение цифр в системе с основанием 2S.

Так как, по условию, r_а ≤ р-1, то для получения свертки потребуется трехразрядный двоичный сумматор, работающий по модулю 5.